Interpretation

Mikis Stasinopoulos
Bob Rigby
Fernanda De Bastiani

Introduction

  • how to interpreted the effect of a single term into the distribution of the response;
  • how to use the GAMLSS model for prediction.

Interpretation

  • how the information we obtain from the fitted model can be used
flowchart TB
  A[Features] --> B(Parameters) 
  B --> D[Properties, \n Characteristics]
  D -->  C(Distribution)
  B --> C
Figure 1: x-variables effecting the properties of the distribution.

graphical Partial effects

  • ceteris paribus

  • \(\textbf{x}_j\) denote a single (or maximum two terms)

  • \(\textbf{x}_{-j}\) all the rest so \(\{\textbf{x}_j, \textbf{x}_{-j} \}\) are all terms in the model

  • \(\omega(D)\) the characteristic of the distribution we are interested \({D}(y | \textbf{x}_j , \textbf{x}_{-j}; \boldsymbol{\theta})\)

  • under scenario, \(\textbf{S}[g()]\).

  • \[{PE}_{\omega({D})}\left( \textbf{x}_{j} | \textbf{S} \left[ g(\textbf{x}_{-j})\right] \right)\]

Example: term plots

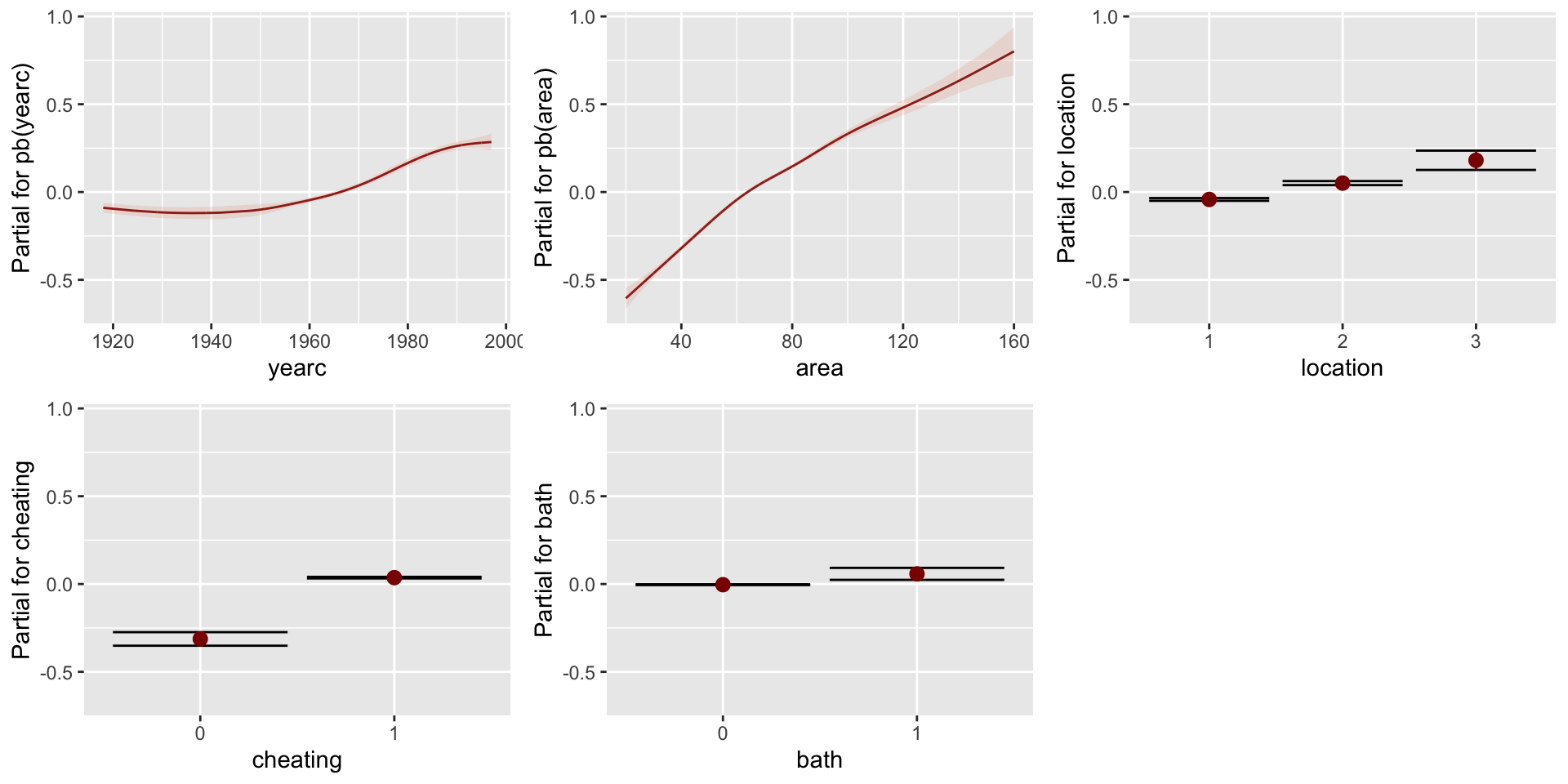
Figure 2: pdf-plot of the fitted am1 mu model

Scenarios

  • fixing values of \(\textbf{x}_{-j}\) (mean or median for continuous, level with more number of observations for factors or other possible values of importance)

  • average over values of \(\textbf{x}_{-j}\)

    • Partial Dependence Plots (PDF), \(\textbf{S}\left[ \text{average}(\textbf{x}_{-j})\right]\)
    • Accumulated Local Effects, (ALE), average ovet the derivatives
    • Marginal Effects (ME) average over local neighbourhood

Characteristics

  • predictors, \(\eta_{\theta_i}\);

  • parameters, \(\theta_i\);

  • moments, mean, variance;

  • quantiles, median;

  • distribution

PE; parameter \(\mu\); add. smooth

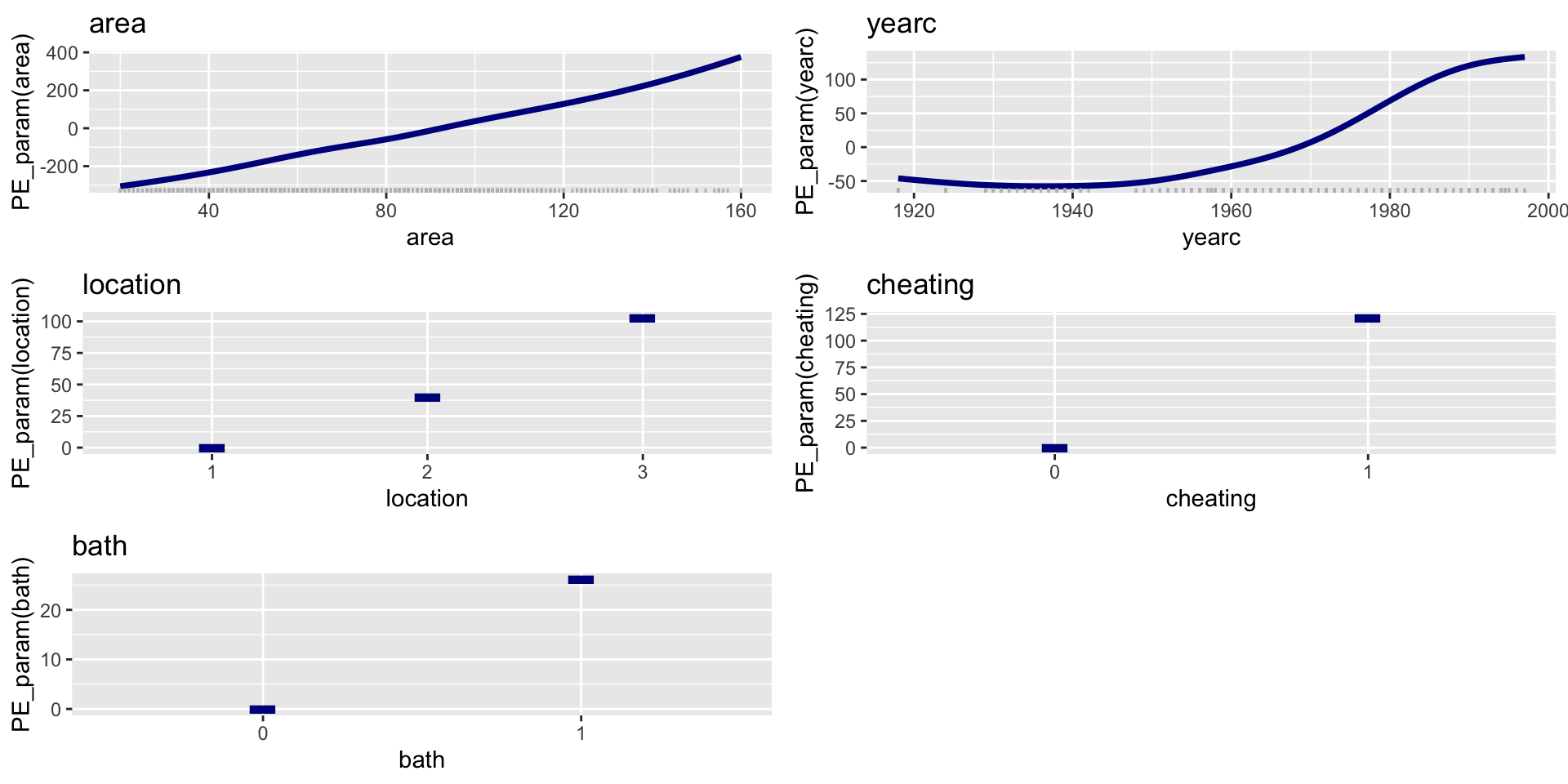
Figure 3: PE for mu for the additive smooth model.

PE; parameter \(\mu\); N. N.

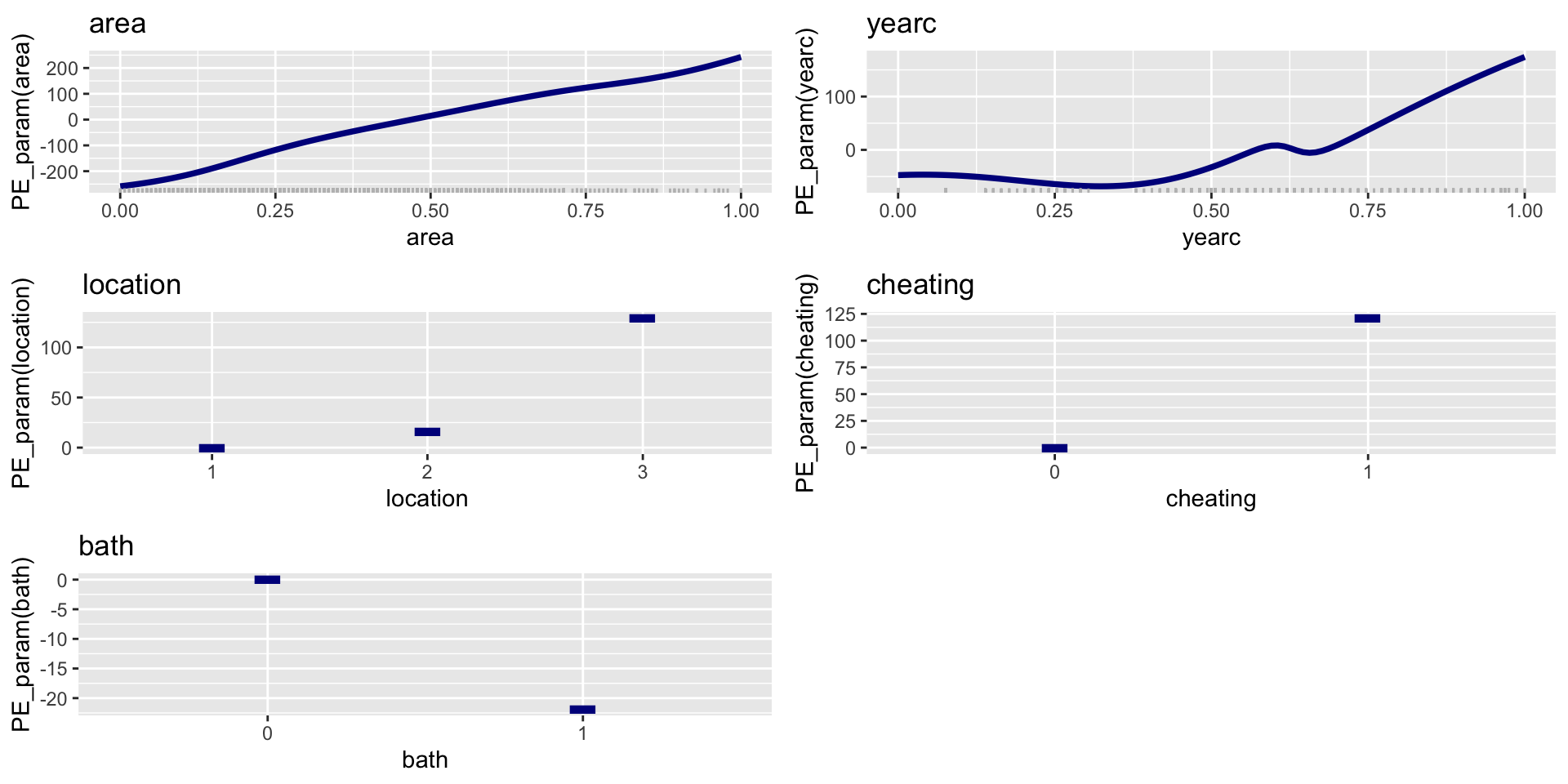
Figure 4: PE for mu for the neural network model.

PE; parameter \(\sigma\); add. sm.

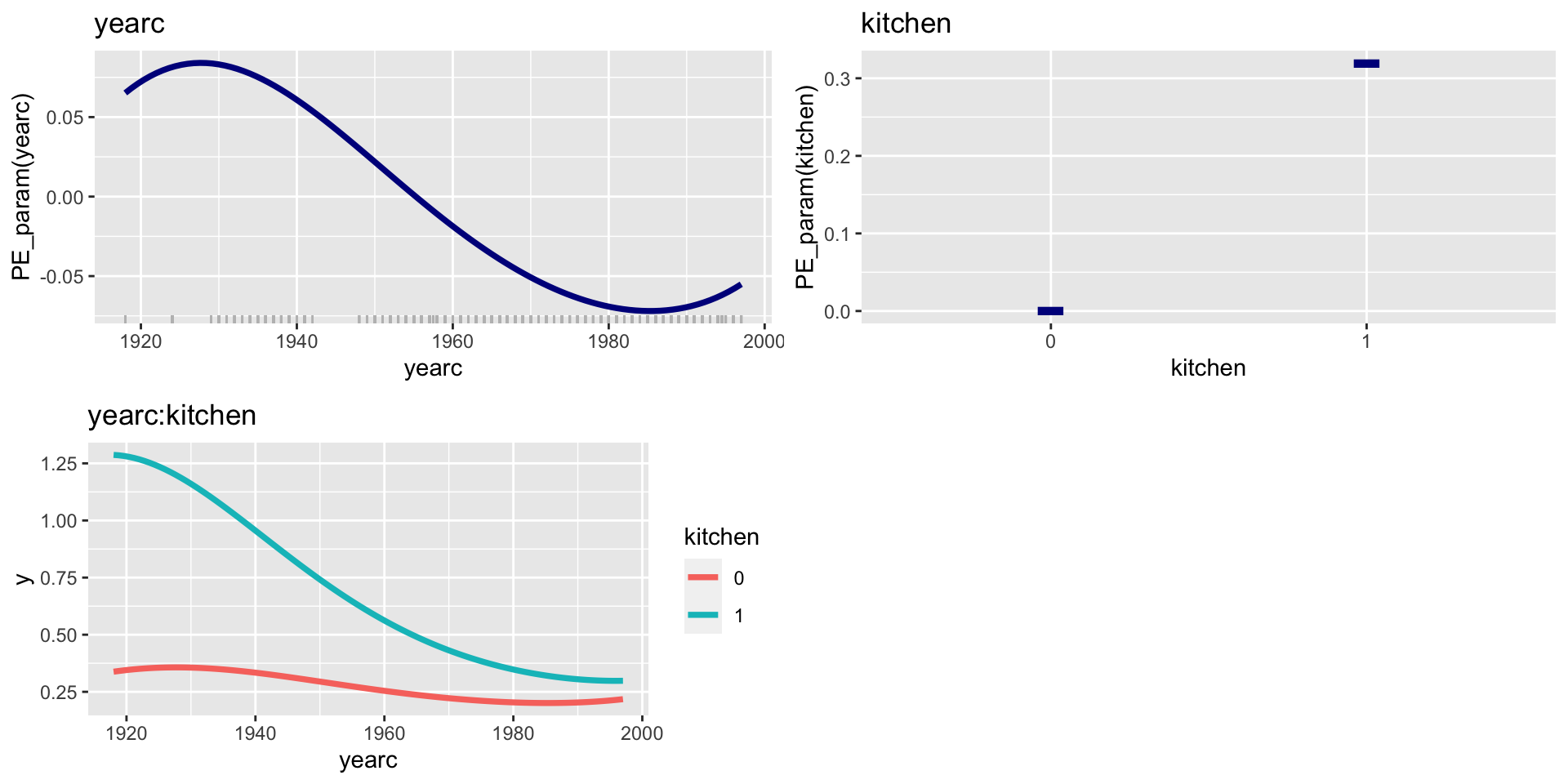
Figure 5: PE for sigma for the additive smooth model

PE; parameter \(\sigma\); N.N.

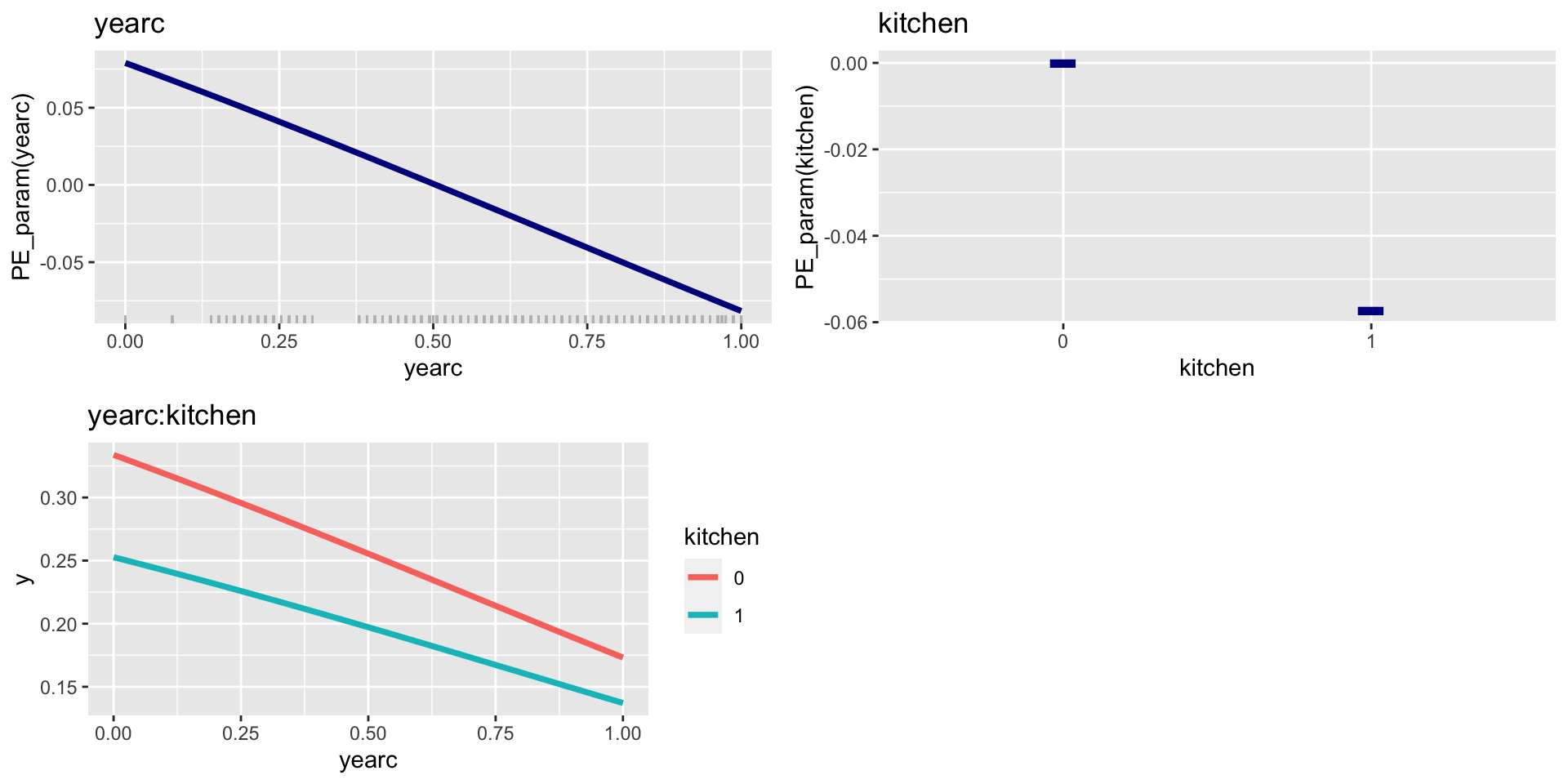
Figure 6: PE for sigma

ALE; parameters \(\mu\); Add. sm.

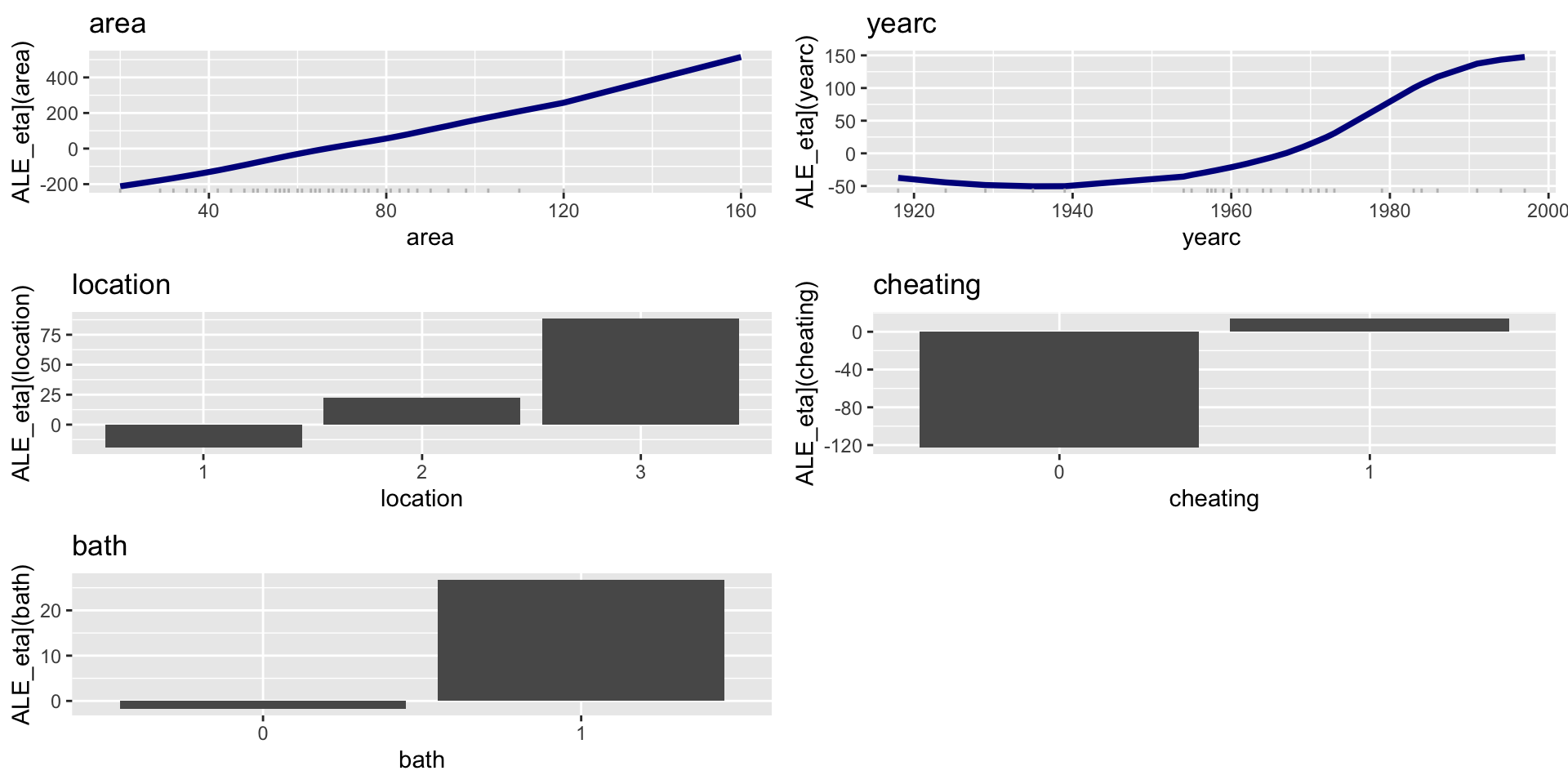
Figure 7: PE for mu modl for mfA1

ALE; parameters \(\mu\); N. N.

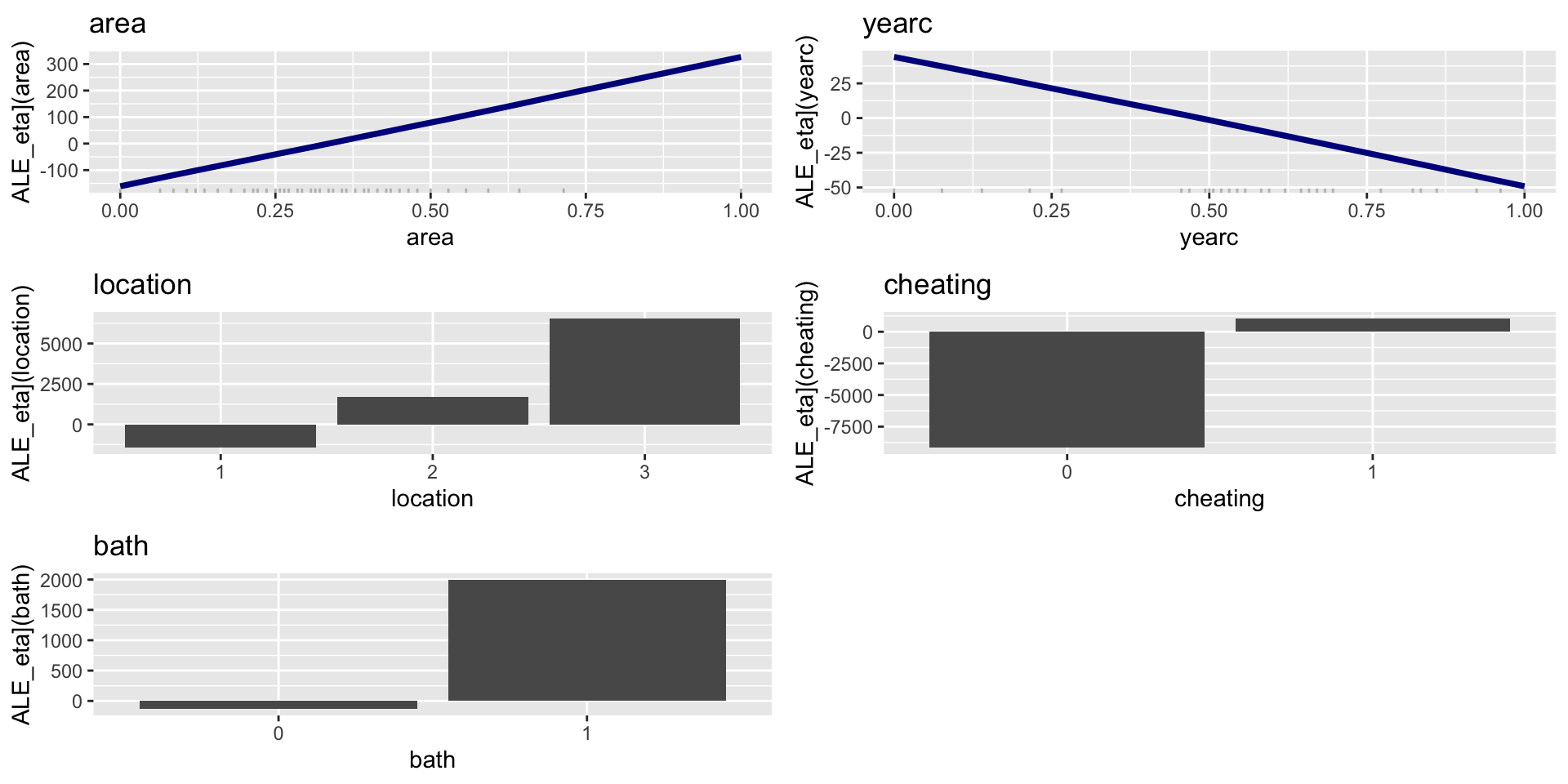
Figure 8: PE for mu modl for mfA1

moments (mean)

  • the BCTo do not always have moments

  • for \(\tau <=2\) the variance do not exist

  • for \(\tau <=1\) the mean do not exist

quantiles, \(\mu\), add. sm.

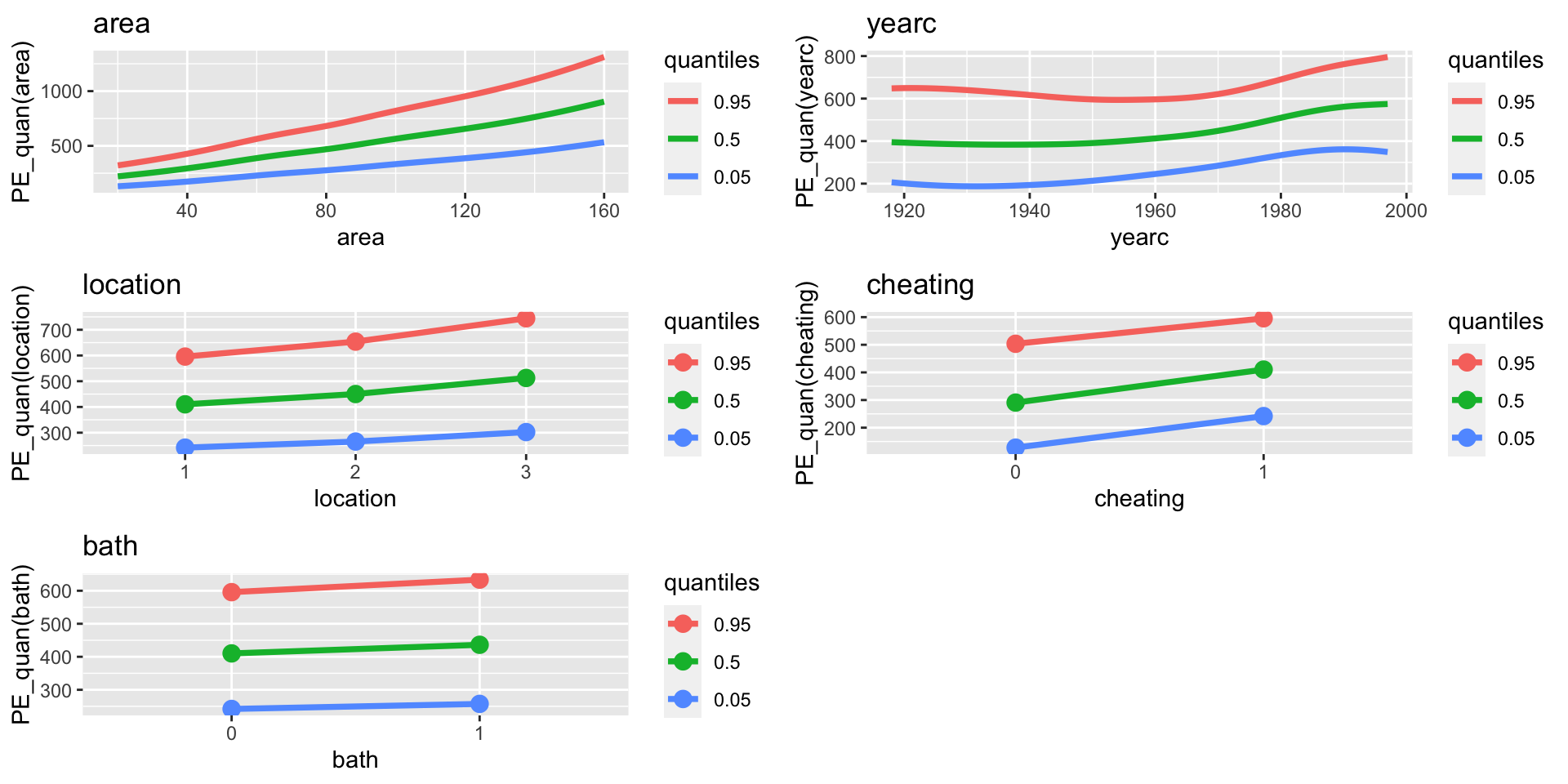
Figure 9: PE-quantiles 95%, 50%, 5% for mu model for mfA1

quantiles, \(\mu\), N.N.

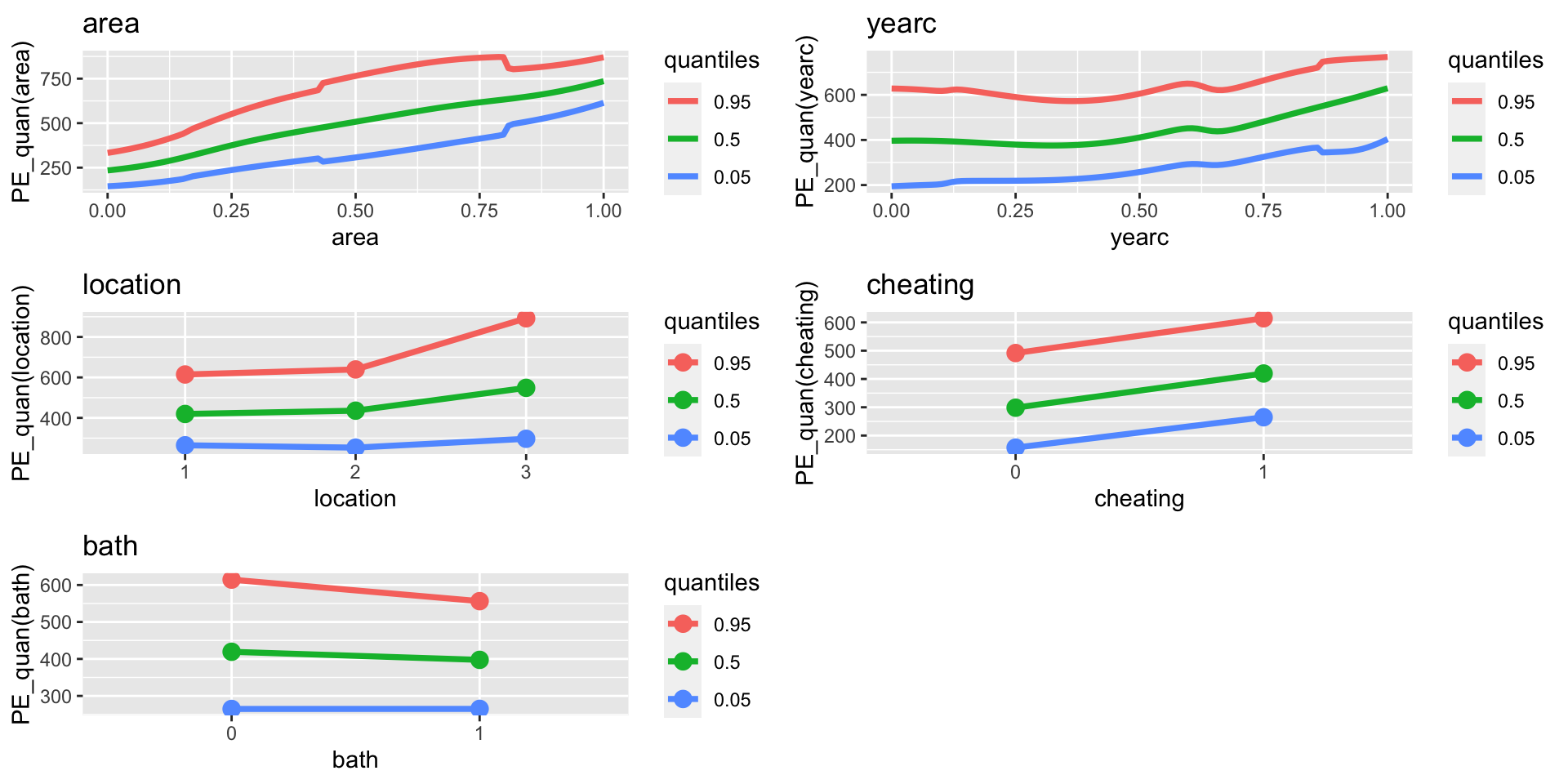
Figure 10: PE-quantiles 95%, 50%, 5% for mu model for mfNN

distributions, \(\mu\), add. sm.

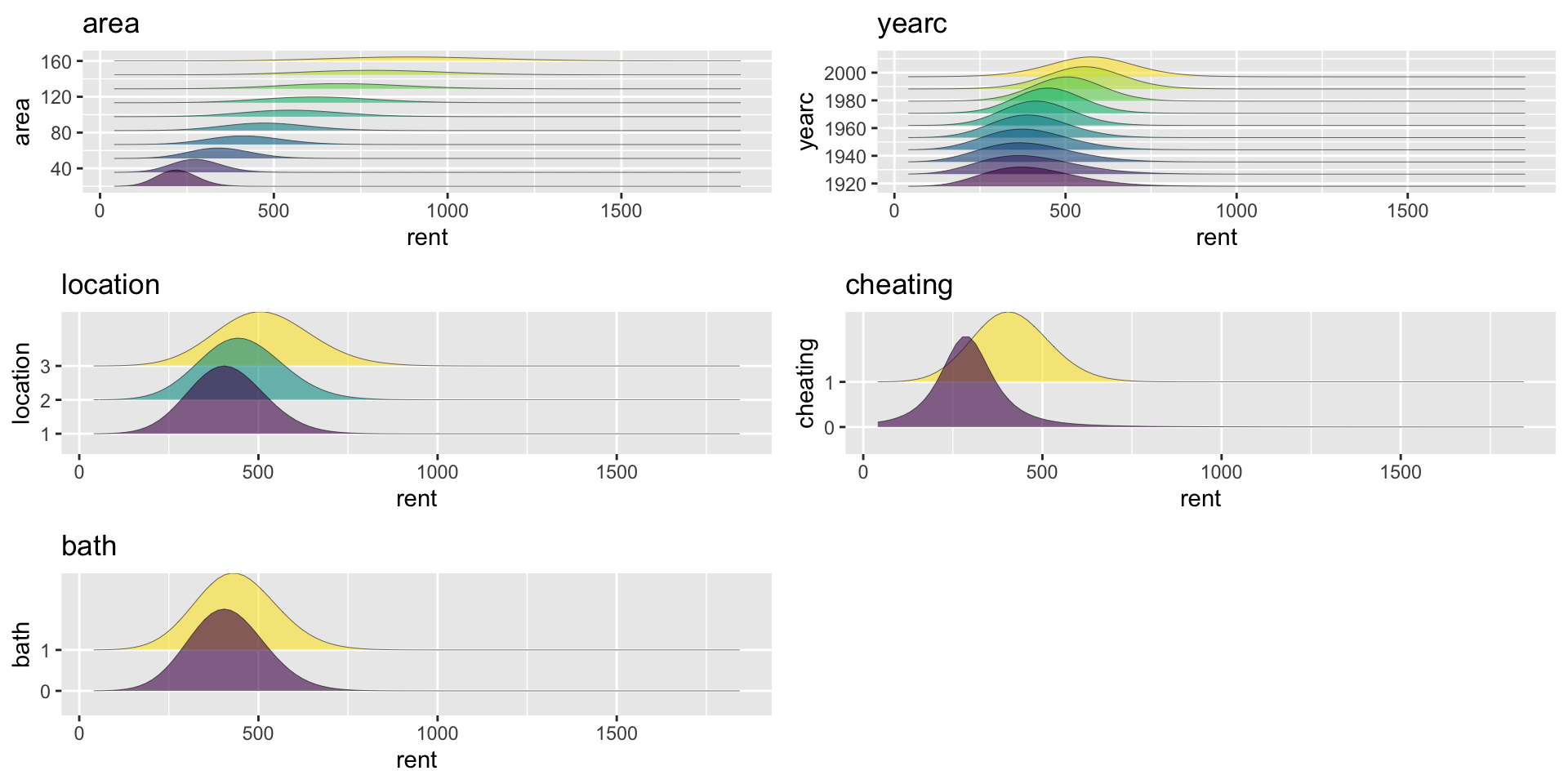
Figure 11: PE-distribution for mu model for mfA1

distributions, \(\mu\), N.N.

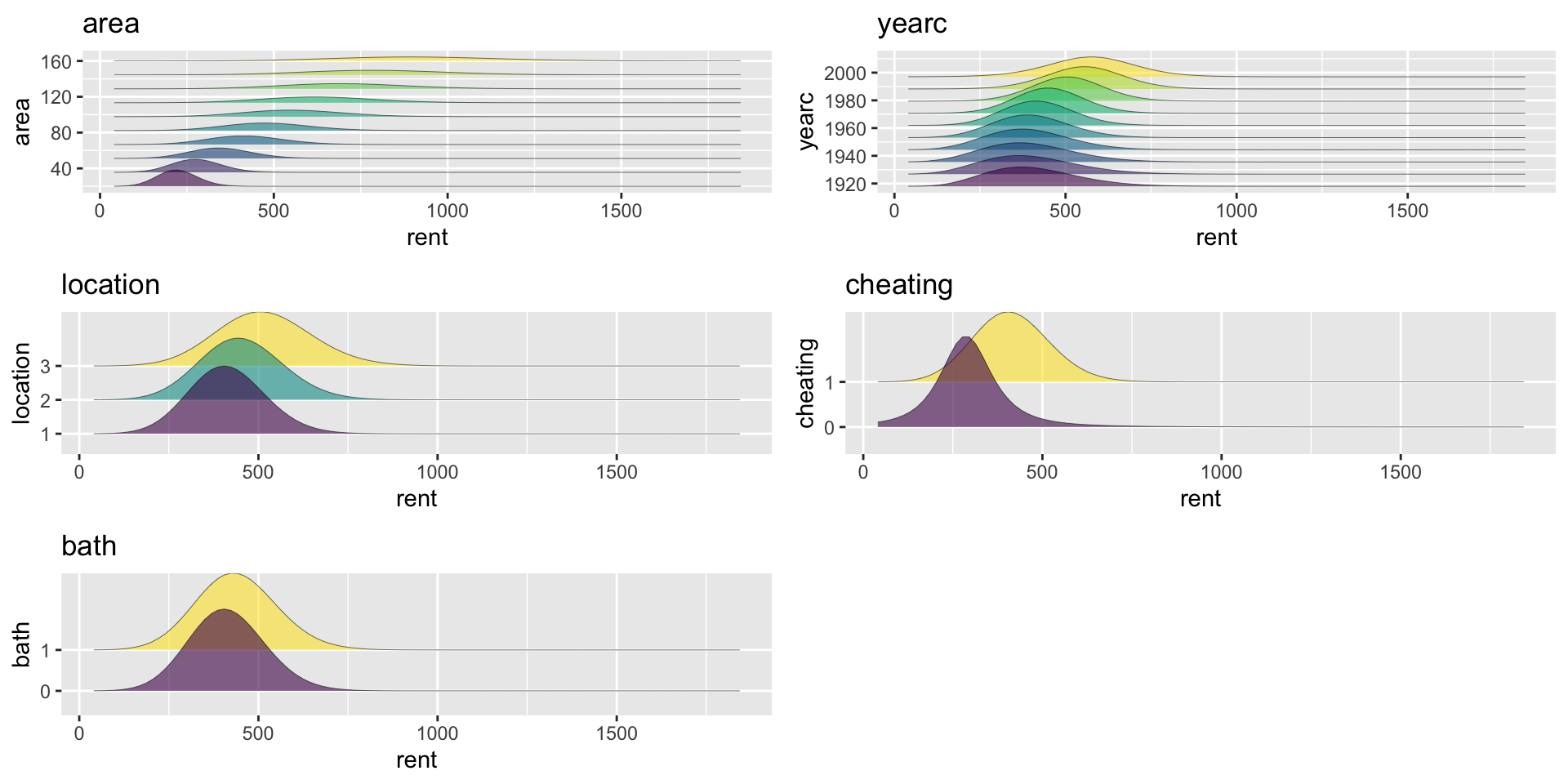
Figure 12: PE-distributions for mu model for mfNN

the purpose of the study

  • the purpose should be always in our mind when we try to analyse any data

  • the Munich rent data are collected almost every 10 years

  • guidance to judges on whether a disputed rent is a fair or not

  • purpose is to identify very low or very hight rents by correcting for the explanatory variables

  • similar in detecting “outliers”

  • a possible solution: prediction z-scores

prediction z-scores

Scenarios

rent area yearc location bath kitchen heating
1500 140 1983 3 1 1 1
1000 55 1915 1 0 0 0
800 65 1960 1 1 1 1

prediction z-scores (con.)

rent <- c(1500, 1000,800)
area <- c(140, 55, 65)
yearc <- c(1983, 1915, 1960)
location <- c(3,1,1)
bath <- c(1,0,1)
kitchen <- c(1,0,1)
cheating <- c(1,0,1)
ndat <- data.frame(rent, area, yearc, location, bath, kitchen, cheating)
cat("prediction z-scores", "\n")
prediction z-scores 
getTGD(mfA1, newdata=ndat)$resid
[1] 0.3088481 3.9675604 3.4323822

summary

GAMLSS can tackle problems where the interest of the investigation lies not in the center but other parts of the distribution.

Personal view for the future of GAMLSS development;

  • theoretical contributions

  • software and

  • knowledge exchange

Summary (continue)

  • theoretical contributions
    • interpretable tools
    • model average for prediction
  • software
    • a neater version of gamlss() to make it easier to incorporate LM algorithms
  • books and knowledge exchange
    • there is need for applied and elementary books
    • more application public health and environment

the team

This is a collaborative work:

working party current past
Gillian Heller Konstantinos Pateras Popi Akantziliotou
Fernanda De Bastiani Paul Eilers Vlasios Voudouris
Thomas Kneib Nikos Kametas Nicoleta Mortan
Achim Zaileis Tim Cole Daniil Kiose
Andreas Mayr Nikos Georgikopoulos Dea-Jin Lee
Nicolaus Umlauf Luiz Nakamura María Xosé Rodríguez-Álvarez
Reto Stauffer Nadja Klein Majid Djennad
Robert Rigby Julian Merder Fiona McElduff
Mikis Stasinopoulos Abu Hossain Raydonal Ospina

end

back to the index

The Books

www.gamlss.com