Fitting

Mikis Stasinopoulos
Bob Rigby
Fernanda De Bastiani

Introduction

  • the basic GAMLSS algorithm
  • different statistical approaches for fitting a GAMLSS model
  • different machine learning techniques for fitting a GAMLSS model.

Machine Learning Models

properties

  • are the standard errors available?

  • do the x’s need standardization.

  • about the algorithm

     - stability
 - speed 
 - convergence

  • nonlinear terms

  • interactions

  • dataset type

  • is the selection of x’s automatic?

  • interpretation

Linear Models

mLM <- gamlss(rent~area+poly(yearc,2)+location+bath+kitchen+
              cheating,
              ~area+yearc+location+bath+kitchen+cheating, 
              family=BCTo, trace=FALSE, data=da)
summary(mLM)

Linear Models

******************************************************************
Family:  c("BCTo", "Box-Cox-t-orig.") 

Call:  gamlss(formula = rent ~ area + poly(yearc, 2) + location +  
    bath + kitchen + cheating, sigma.formula = ~area +  
    yearc + location + bath + kitchen + cheating, family = BCTo,  
    data = da, trace = FALSE) 

Fitting method: RS() 

------------------------------------------------------------------
Mu link function:  log
Mu Coefficients:
                 Estimate Std. Error t value Pr(>|t|)    
(Intercept)     5.0138582  0.0277852 180.451  < 2e-16 ***
area            0.0106311  0.0002331  45.613  < 2e-16 ***
poly(yearc, 2)1 5.0382576  0.3360044  14.995  < 2e-16 ***
poly(yearc, 2)2 3.3475762  0.2737237  12.230  < 2e-16 ***
location2       0.0875504  0.0102485   8.543  < 2e-16 ***
location3       0.1967006  0.0385032   5.109 3.44e-07 ***
bath1           0.0415393  0.0219353   1.894   0.0584 .  
kitchen1        0.1120385  0.0243199   4.607 4.25e-06 ***
cheating1       0.3297044  0.0243422  13.545  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

------------------------------------------------------------------
Sigma link function:  log
Sigma Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) 10.4022601  0.7528378  13.817  < 2e-16 ***
area         0.0012116  0.0006135   1.975   0.0484 *  
yearc       -0.0059332  0.0003864 -15.356  < 2e-16 ***
location2    0.0595118  0.0254048   2.343   0.0192 *  
location3    0.2191754  0.0930995   2.354   0.0186 *  
bath1        0.0058254  0.0087229   0.668   0.5043    
kitchen1     0.0400246  0.0882200   0.454   0.6501    
cheating1   -0.2453139  0.0487224  -5.035 5.06e-07 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

------------------------------------------------------------------
Nu link function:  identity 
Nu Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.65631    0.05598   11.72   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

------------------------------------------------------------------
Tau link function:  log 
Tau Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   3.2918     0.4411   7.463 1.09e-13 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

------------------------------------------------------------------
No. of observations in the fit:  3082 
Degrees of Freedom for the fit:  19
      Residual Deg. of Freedom:  3063 
                      at cycle:  10 
 
Global Deviance:     38254.51 
            AIC:     38292.51 
            SBC:     38407.14 
******************************************************************

Additive Models

mAM <- gamlss(rent~pb(area)+pb(yearc)+location+bath+kitchen+
                cheating,
      ~pb(area)+pb(yearc)+location+bath+kitchen+cheating, 
              family=BCTo, data=da, trace=F)
AIC(mLM, mAM)

Additive Models

          df      AIC
mAM 29.78058 38198.79
mLM 19.00000 38292.51

Additive Models (continue)

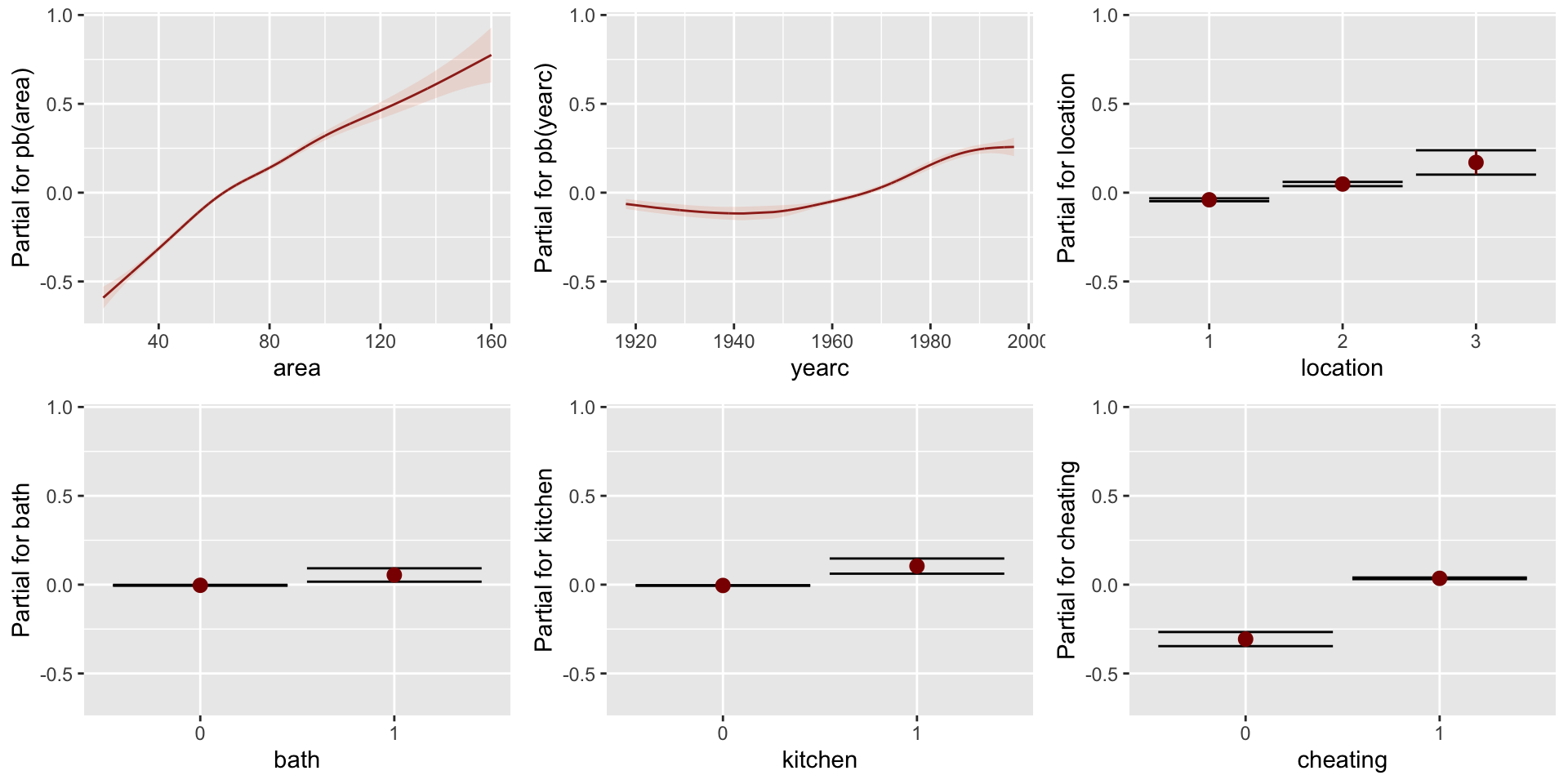
Figure 1: pdf-plot of the fitted am1 mu model

Additive Models (continue)

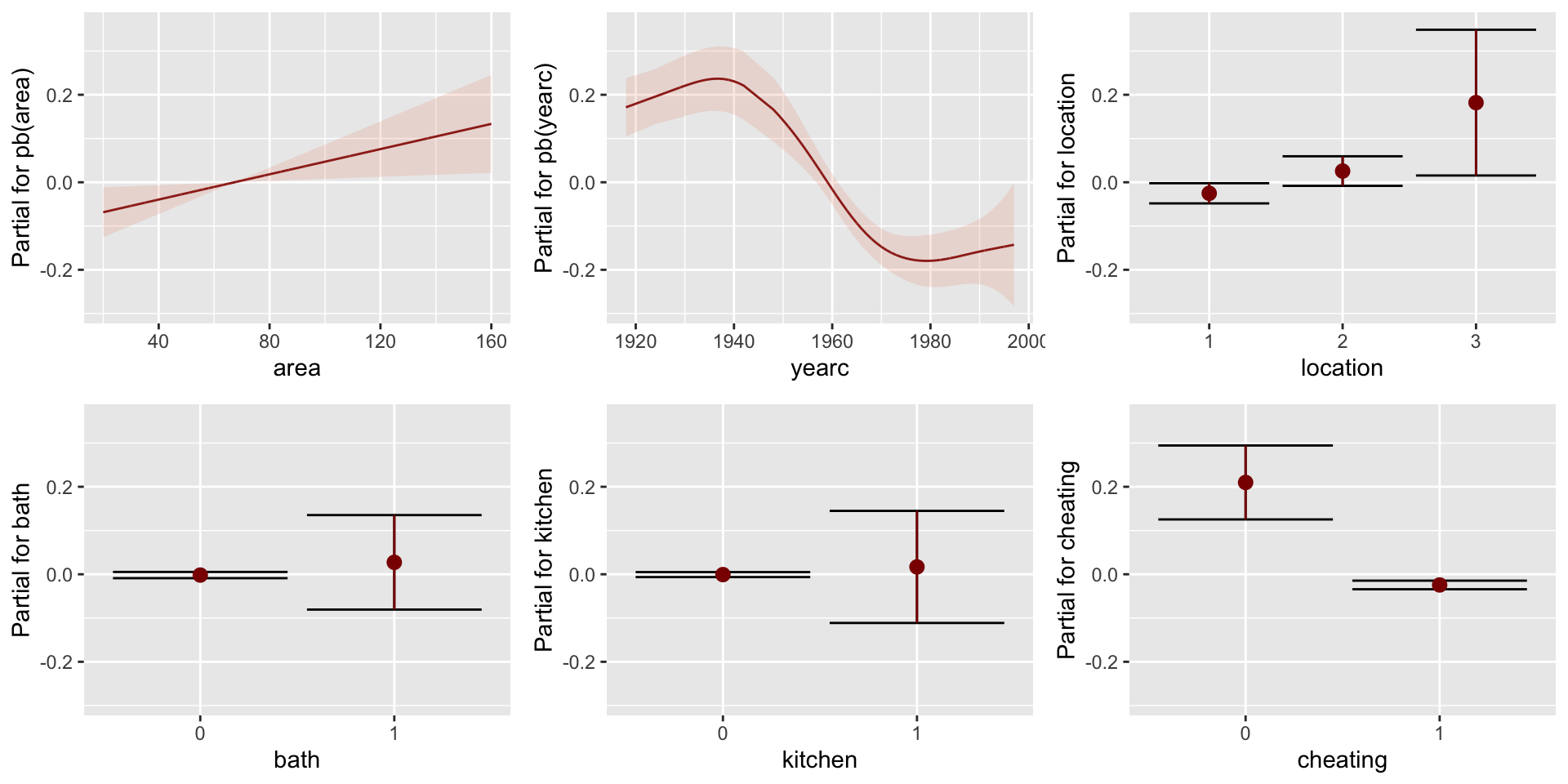
Figure 2: pdf-plot of the fitted am1 sigma model

Regression Trees

library(gamlss.add)
mRT <- gamlss(rent~tr(~area+yearc+location+bath+kitchen+cheating),~tr(~area+yearc+location+bath+kitchen+cheating), 
              family=BCTo, data=da, trace=FALSE)
AIC(mLM, mAM, mRT)

Regression Trees

          df      AIC
mAM 29.78058 38198.79
mLM 19.00000 38292.51
mRT 22.00000 38711.66

Regression Trees (continue)

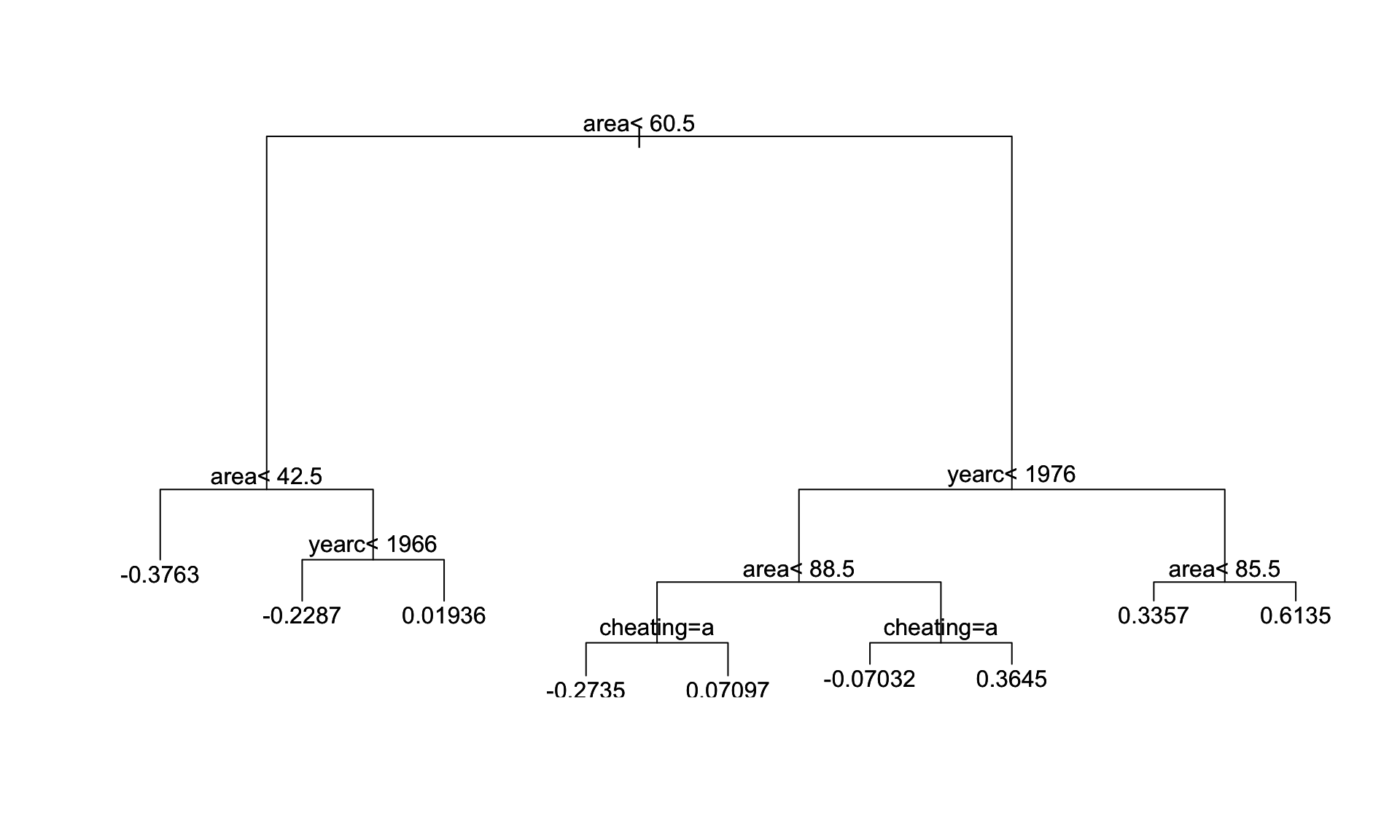
Figure 3: The fitted tree for mu model

Regression Trees (continue)

Figure 4: The fitted tree for mu model

Neural Networks

 source("~/Dropbox/github/gamlss-ggplots/R/data_stand.R")
da01 <- data_scale(da, response=rent, scale = "0to1" )
library(gamlss.add)
set.seed(213)
mNN <- gamlss(rent~nn(~area+yearc+location+bath+kitchen+
                         cheating, size=5),
                  ~nn(~area+yearc+location+bath+kitchen+cheating), 
              family=BCTo, data=da01)

Neural Networks

GAMLSS-RS iteration 1: Global Deviance = 38089.89 
GAMLSS-RS iteration 2: Global Deviance = 38054.95 
GAMLSS-RS iteration 3: Global Deviance = 38054.1 
GAMLSS-RS iteration 4: Global Deviance = 38053.9 
GAMLSS-RS iteration 5: Global Deviance = 38053.84 
GAMLSS-RS iteration 6: Global Deviance = 38053.79 
GAMLSS-RS iteration 7: Global Deviance = 38053.78 
GAMLSS-RS iteration 8: Global Deviance = 38053.78 
GAMLSS-RS iteration 9: Global Deviance = 38053.78 
AIC(mLM, mAM, mRT, mNN)
          df      AIC
mAM 29.78058 38198.79
mNN 78.00000 38209.78
mLM 19.00000 38292.51
mRT 22.00000 38711.66

Neural Networks (continue)

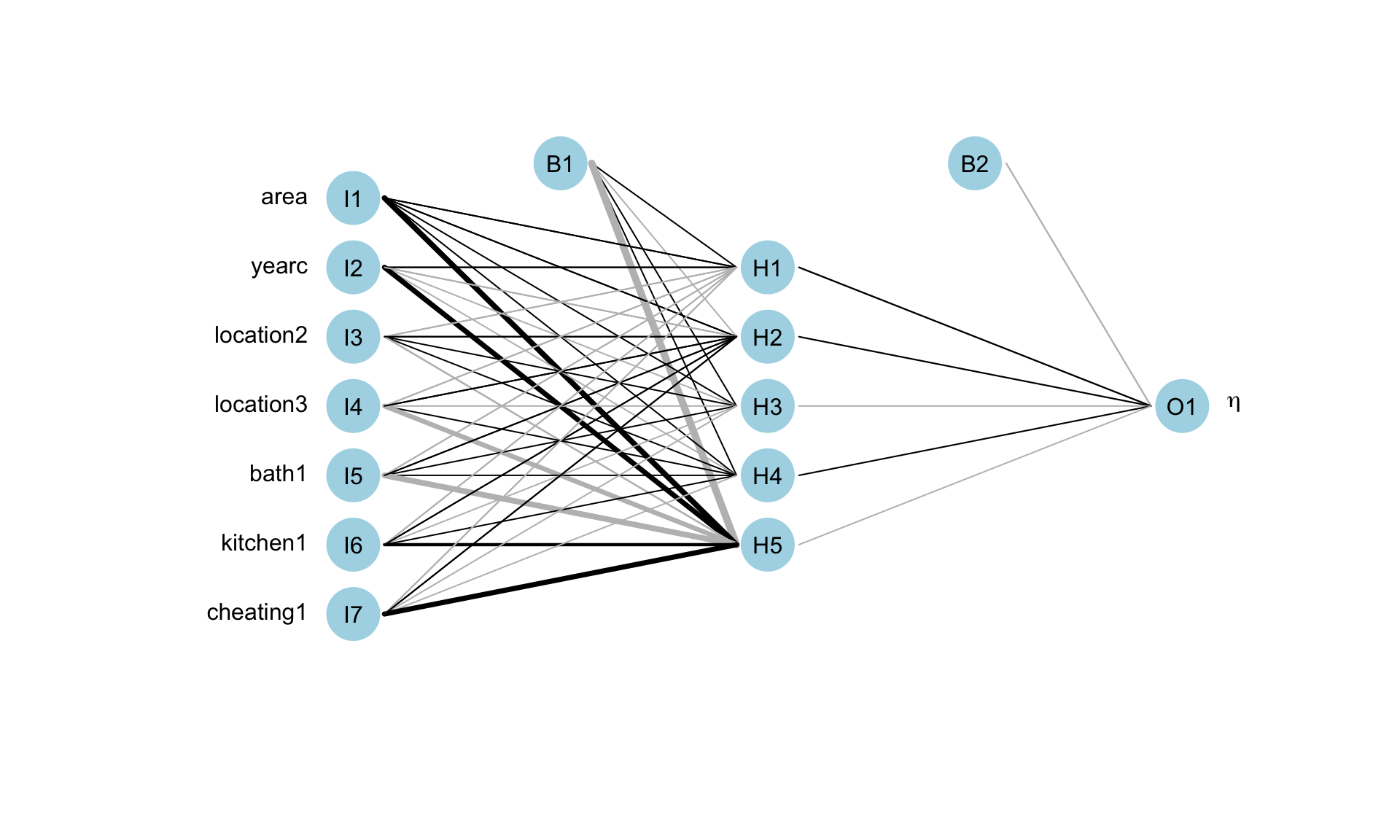
Figure 5: The fitted neural network model fot mu.

Neural Networks

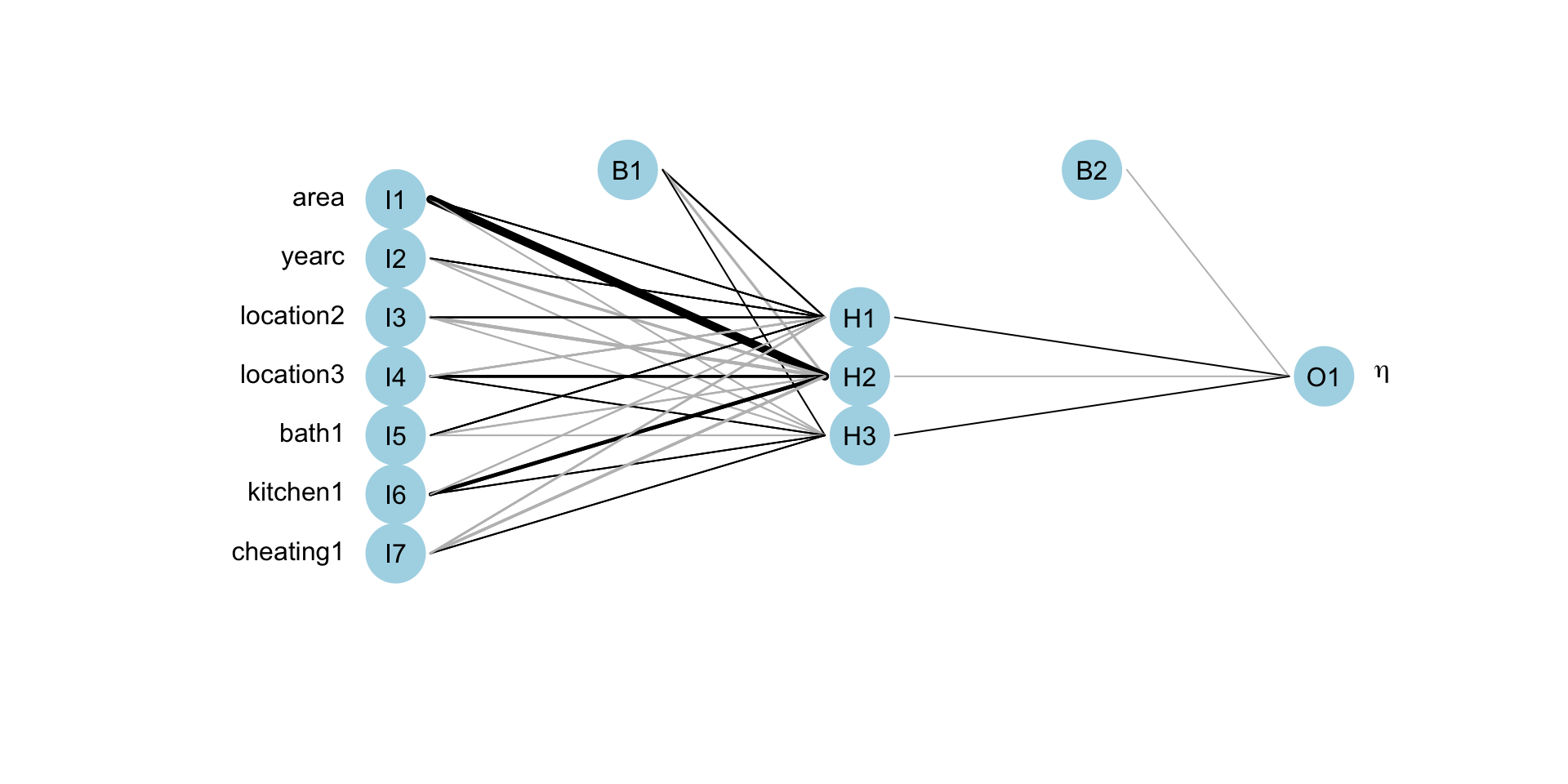
Figure 6: The fitted neural network model fot sigma.

LASSO

library(gamlss.lasso)
source("~/Dropbox/github/gamlss-ggplots/R/data_stand.R")
da10 <- data_scale(da, response=rent)
da1 <- data_form2df(da10,  response=rent, type="main.effect", 
                   nonlinear="TRUE", arg=3)
mLASSO <- gamlss(rent~gnet(x.vars=names(da1)[-c(1)],
                    method = "IC", ICpen="BIC"),
                     ~gnet(x.vars=names(da1)[-c(1)],
                     method = "IC", ICpen="BIC"),
                 data=da1, family=BCTo, bf.cyc=1, 
                c.crit=0.1, trace=FALSE)
AIC(mLM, mAM, mRT, mNN,  mLASSO)

LASSO

             df      AIC
mAM    29.78058 38198.79
mNN    78.00000 38209.78
mLM    19.00000 38292.51
mLASSO 22.00000 38309.11
mRT    22.00000 38711.66

LASSO (continue)

source("~/Dropbox/GAMLSS-development/glmnet/sumplementary_functions_for_gnet.R")
gnet_terms(mLASSO)

LASSO (continue)

      area1       area2       area3      yearc1      yearc2      yearc3 
13.72498782 -1.85175963  0.09162263  4.97838839  3.71690657 -0.18975745 
  location2   location3   cheating1 
 0.01331635  0.05631020  0.27463624 
gnet_terms(mLASSO, "sigma")
     area1      area2      area3     yearc1     yearc3  location2  location3 
 2.2850872 -0.5173168  1.6240863 -7.7665983  3.2776033  0.0673355  0.3178812 
  kitchen1  cheating1 
 0.1209266 -0.1497227

Principal Component Regression

library(gamlss.foreach)
registerDoParallel(cores = 10)
source("~/Dropbox/github/gamlss-ggplots/R/data_stand.R")
source("~/Dropbox/GAMLSS-development/PCR/GAMLSS-pc.R")
X = formula2X(rent~area+yearc+location+bath+kitchen+
              cheating, data=da)
mPCR <- gamlss(rent~pc(x=X),~pc(x=X),
    data=da1, family=BCTo, bf.cyc=1, trace=TRUE)

Principal Component Regression

GAMLSS-RS iteration 1: Global Deviance = 38458.91 
GAMLSS-RS iteration 2: Global Deviance = 38404.13 
GAMLSS-RS iteration 3: Global Deviance = 38405.09 
GAMLSS-RS iteration 4: Global Deviance = 38404.56 
GAMLSS-RS iteration 5: Global Deviance = 38404.43 
GAMLSS-RS iteration 6: Global Deviance = 38404.38 
GAMLSS-RS iteration 7: Global Deviance = 38404.37 
GAMLSS-RS iteration 8: Global Deviance = 38404.36 
GAMLSS-RS iteration 9: Global Deviance = 38404.36 
GAMLSS-RS iteration 10: Global Deviance = 38404.36 
GAIC(mLM, mAM, mRT, mNN,  mLASSO, mPCR)
             df      AIC
mAM    29.78058 38198.79
mNN    78.00000 38209.78
mLM    19.00000 38292.51
mLASSO 22.00000 38309.11
mPCR   15.00000 38434.36
mRT    22.00000 38711.66

summary

Table 1: Summary of properties of the machine learning algorithms
ML Models coef. s.e. stand. of x’s algo. stab., speed, conv. non-linear terms inter- actions data type auto sele-ction interpre- tation
linear yes no yes, fast, v.good poly declare \(n>r\) no v. easy
additive no no yes, slow, good smooth declare \(n>r\) no easy
RT no no no, slow, bad trees auto \(n>r\)?? yes easy

summary (continue)

Table 2: Summary of properties of the machine learning algorithms
ML Models coef. s.e. stand. of x’s algo. stab., speed, conv. non-linear terms inter- actions data type auto sele-ction interpre- tation
NN no 0 to 1 no, \(\,\,\) ok, \(\,\,\) ok auto auto both? yes v. hard
PCR yes yes yes, fast, good poly declare both auto hard
LASSO no yes yes, fast, good poly declare both auto easy

summary (continue)

Table 3: Summary of properties of the machine learning algorithms
ML Models coef. s.e. stand. of x’s algo. stab., speed, conv. non-linear terms inter- actions data type auto sele-ction interpre- tation
Boost no no yes, fast, good smooth trees declare \(n<<r\) yes easy
MCMC yes no good, ok, \(\,\,\) ok smooth declare \(n>r\) no easy

diagram

flowchart TB
  A[Data] --> B(n greater than r) 
  A --> C( n less than r)
  B --> D[LM,GLM, \n GAM, NN ]
  C --> E[RidgeR, LASSO, Elastic Net, \n PCR, RF, \n Boosting, NN]
Figure 7: Different ways to estimate the coefficients of a GAMLSS model.

end

back to the index

The Books

www.gamlss.com