Comparison

Mikis Stasinopoulos

Bob Rigby

Fernanda De Bastiani

Introduction

• graphical diagnostic tools;
• model summary statistics

Graphical Diagnostic tools

• within model diagnostics

• between model diagnostics

The majority of model diagnostics are based on the model residuals

Residuals

• the standard (training) residual, \((y-\mu)\), is no good for distribution regression models

• PIT residuals; \(u_i=F\left(y_i|\hat{\boldsymbol{\theta}}_i(\textbf{x}_i)\right)\) where \(F()\) is the assumed (cdf)

• if the model is correct, \(u_i\sim U_{[0,1]}\) (uniform)

• z-scores \(z_i=F^{-1}_N(u_i),\)

• if the model is correct, \(z_i\sim N(0,1)\)

• the z-scores also called (randomised) normalised residuals

within model diagnostics

• residuals against variables i.e index, x-variables, fitted \(\mu\) etc; go to figure 13.1

• the density function of the residuals; go to figure 13.2

• the ecdf of the residuals;

• the function dtop(), de-trended Own’s plot; go to figure 13.3

• the QQ-plot;

• the worm plot; go to figure 13.4

• the bucket plot; go to figure 13.5

• the ACF and PACF plots; go to figure 13.6

between models diagnostics

• model density plots; go to figure 13.7

• model QQ-plots; go to figure 13.8

• model worm plots; go to figure 13.9

• model bucket plots; go to figure 13.10

• model principal component plots; go to figure 13.11

• for different values of the explanatory variables

  • continuous go to figure 13.12

  • factors go to figure 13.13

Model Comparison Statistics

• no partition of data is required

  • \[GAIC= \hat{GD}+ k \times df, \] evaluated in the training dataset

• partition of data is required

  • Mean Absolute Prediction Error (MAPE)
  • Likelihod score (LS) \(\sim\) Prediction Global Deviance
  • Continuous Rank Probabily Score (CRPS)

GAIC

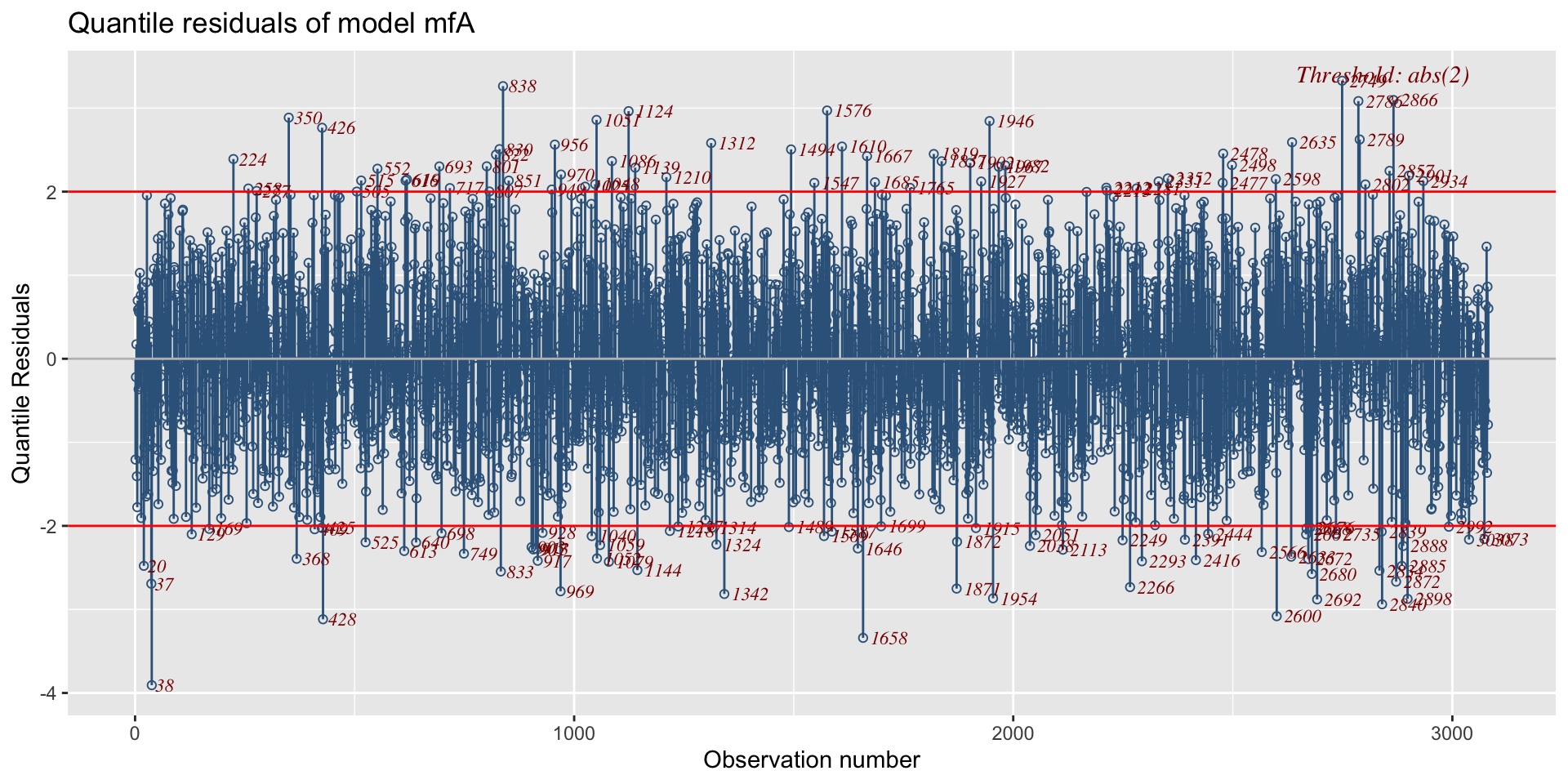
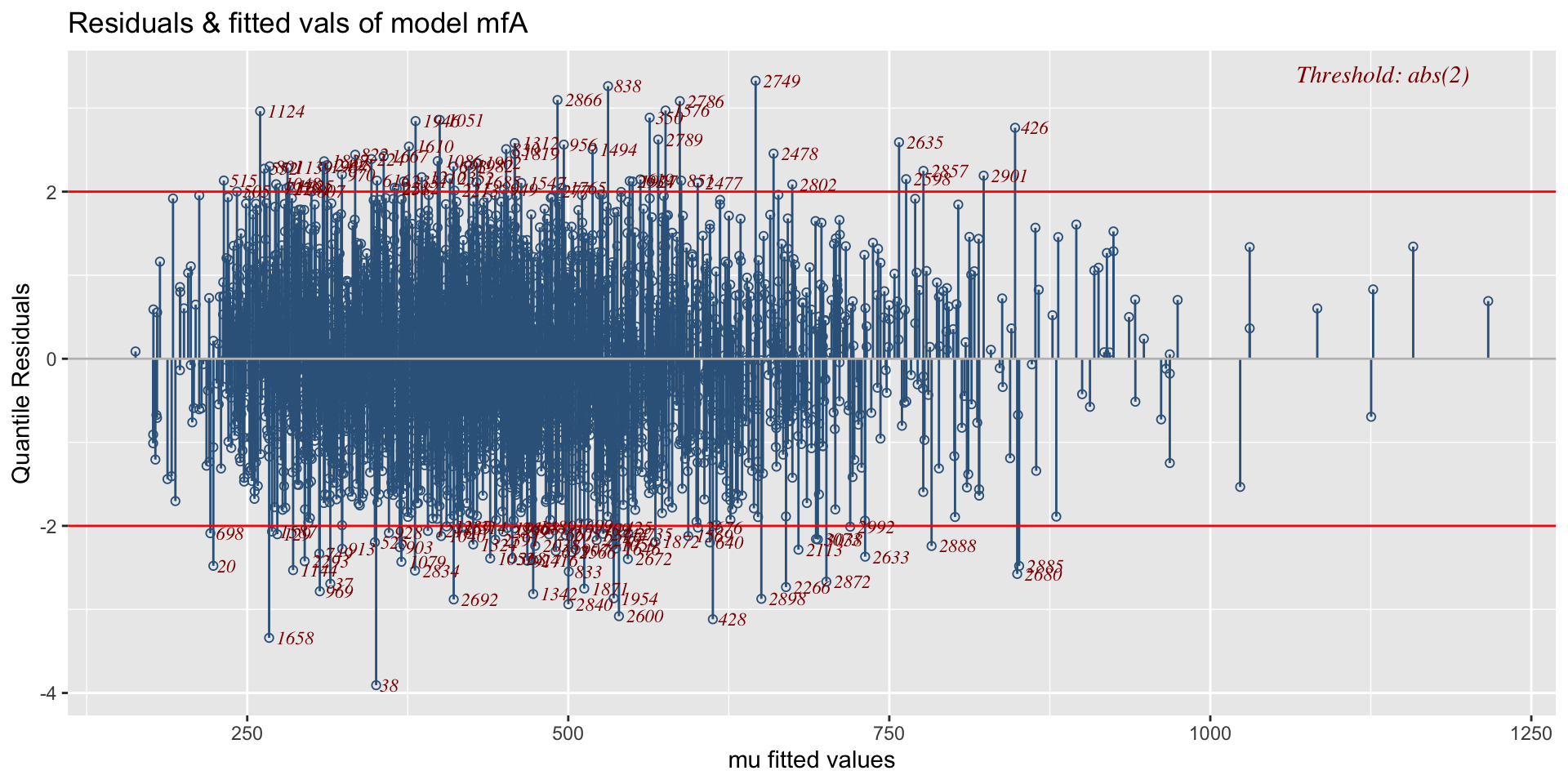
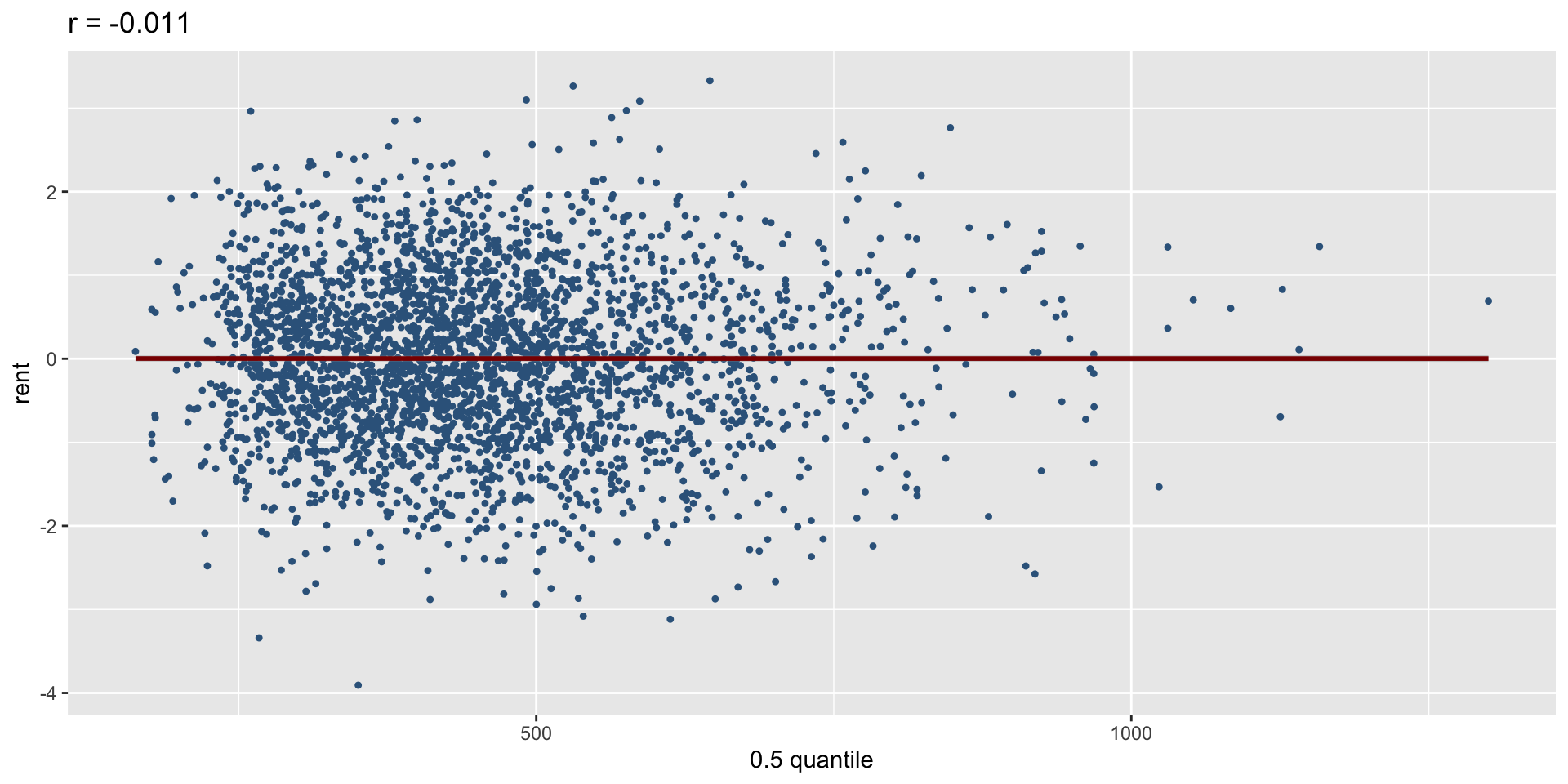
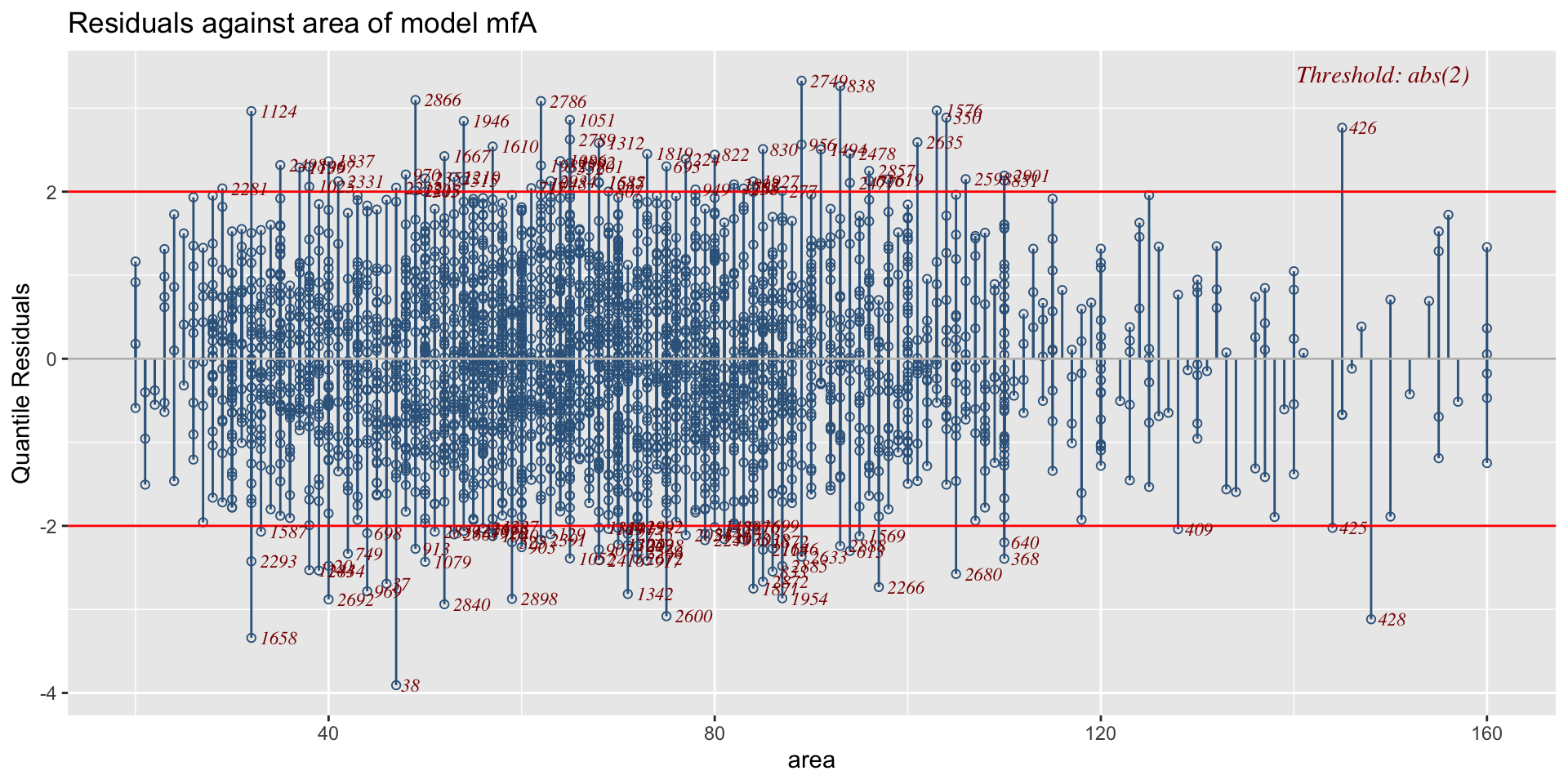
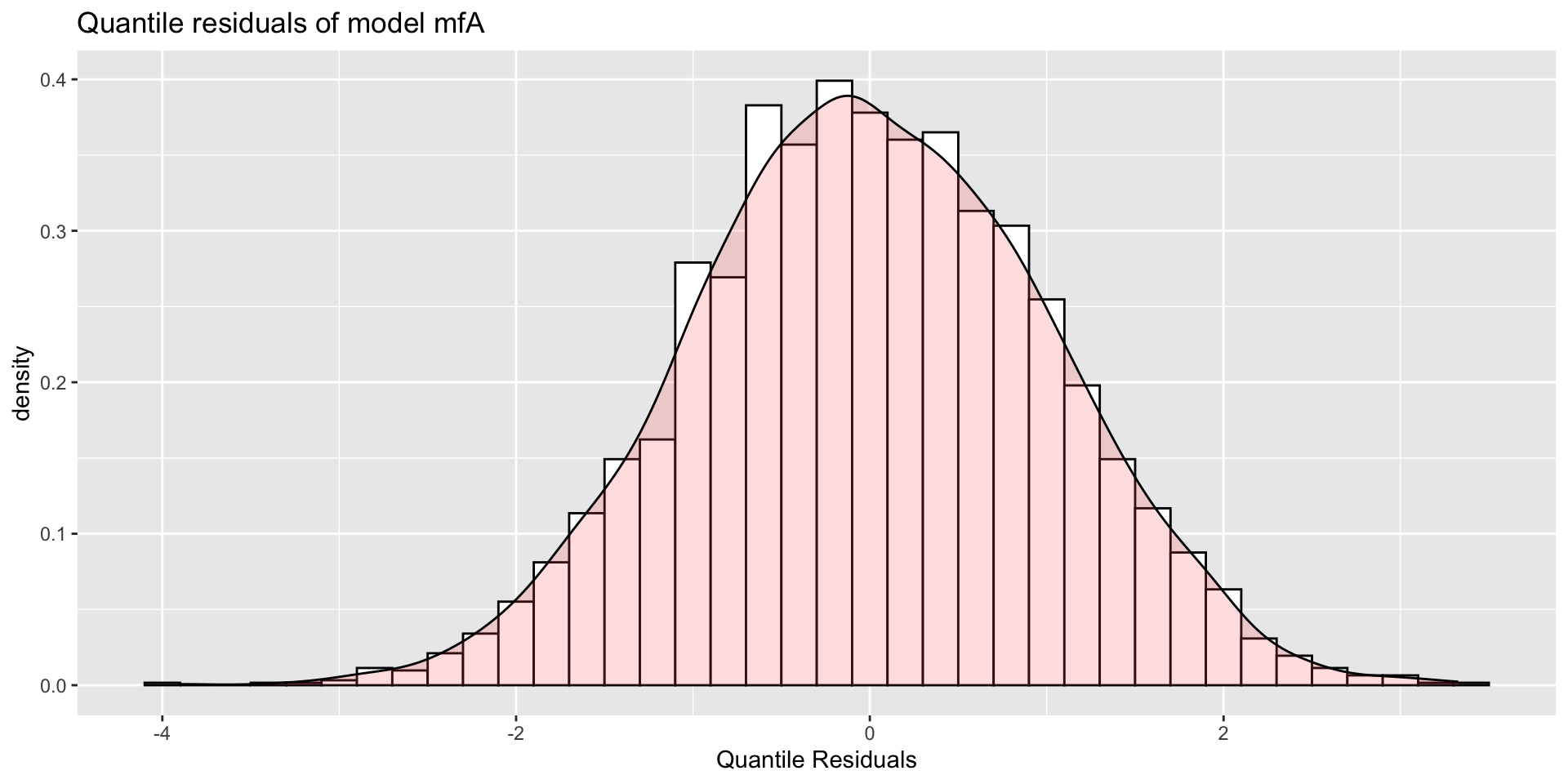
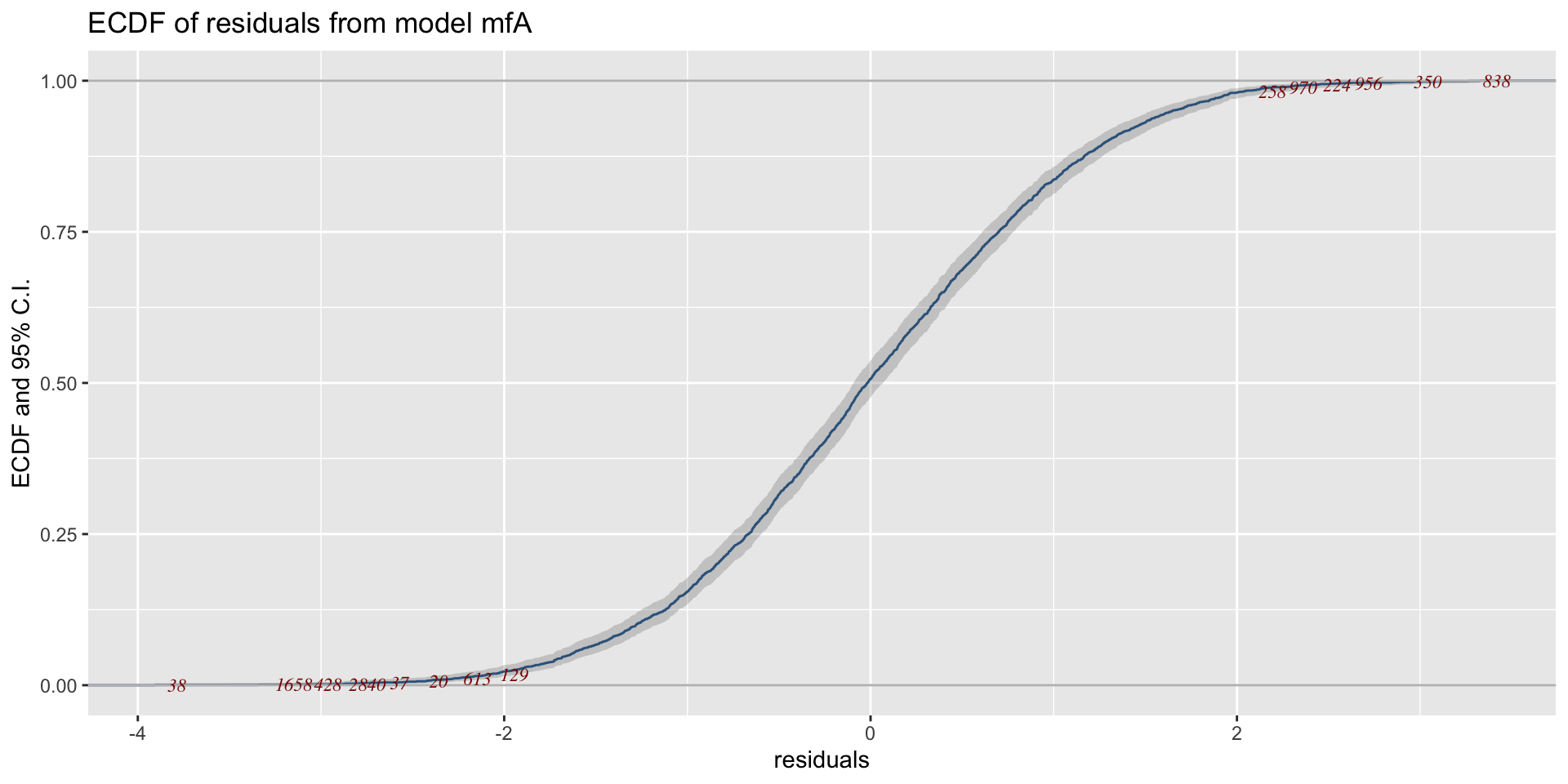
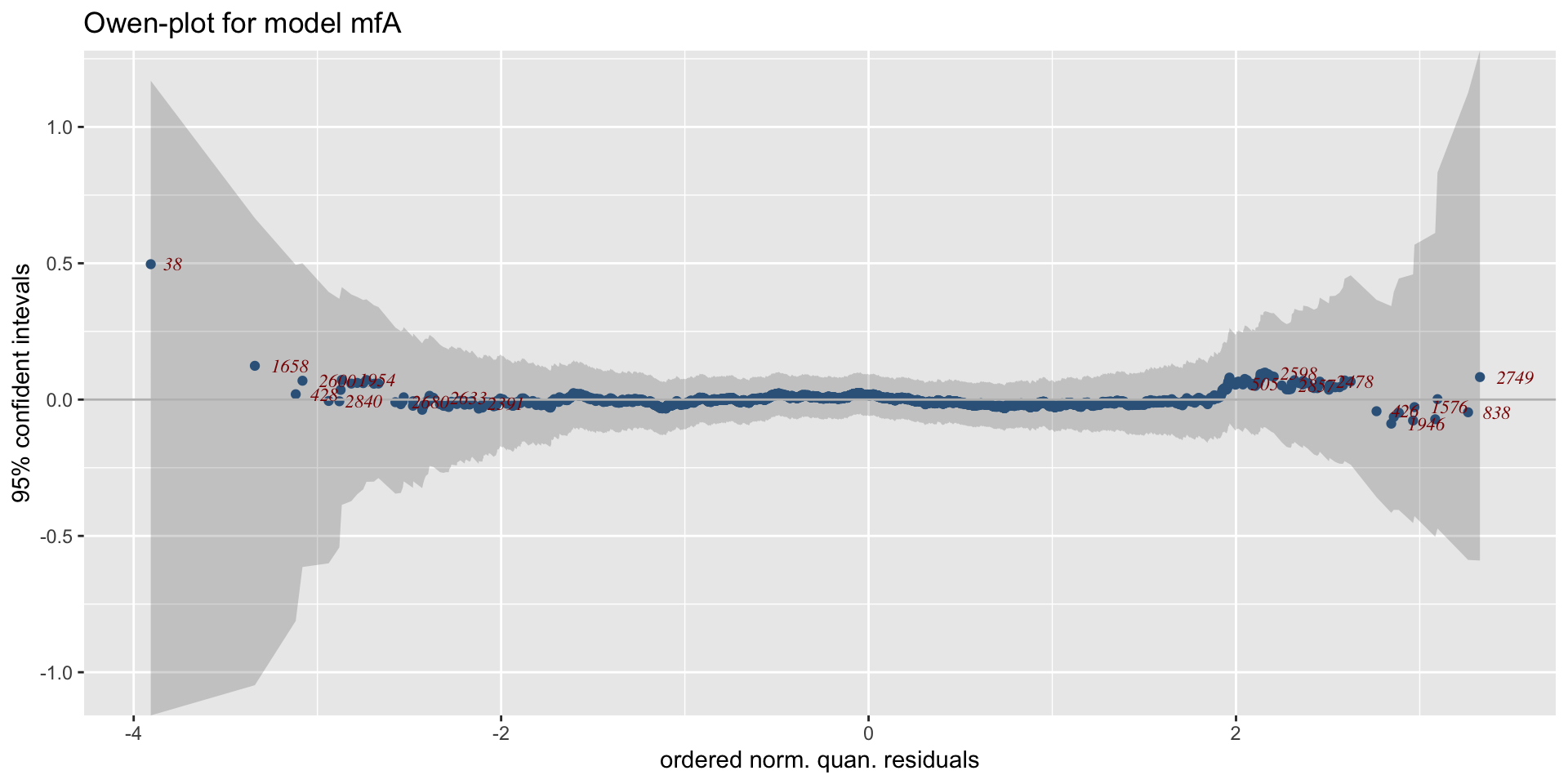
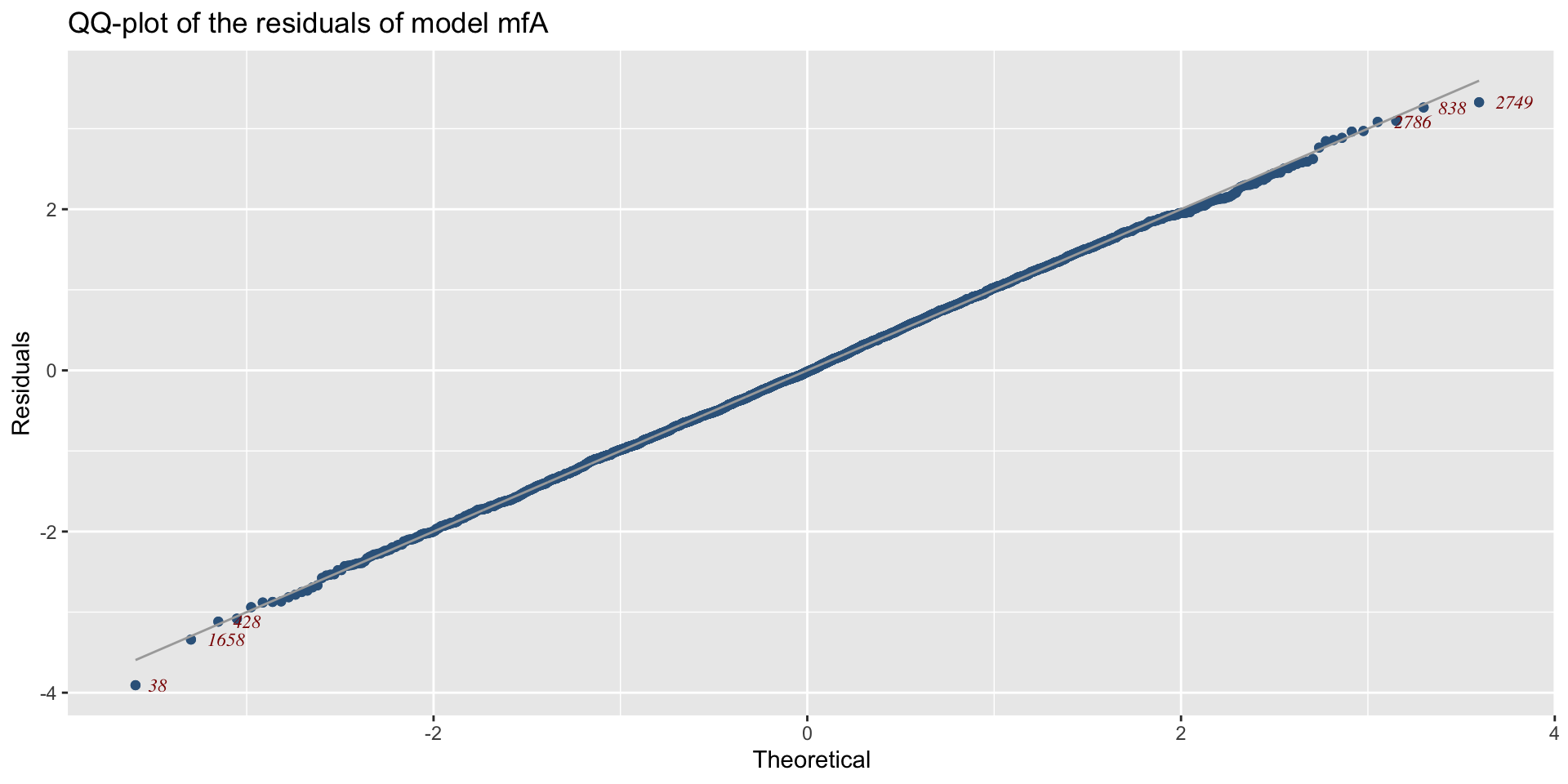
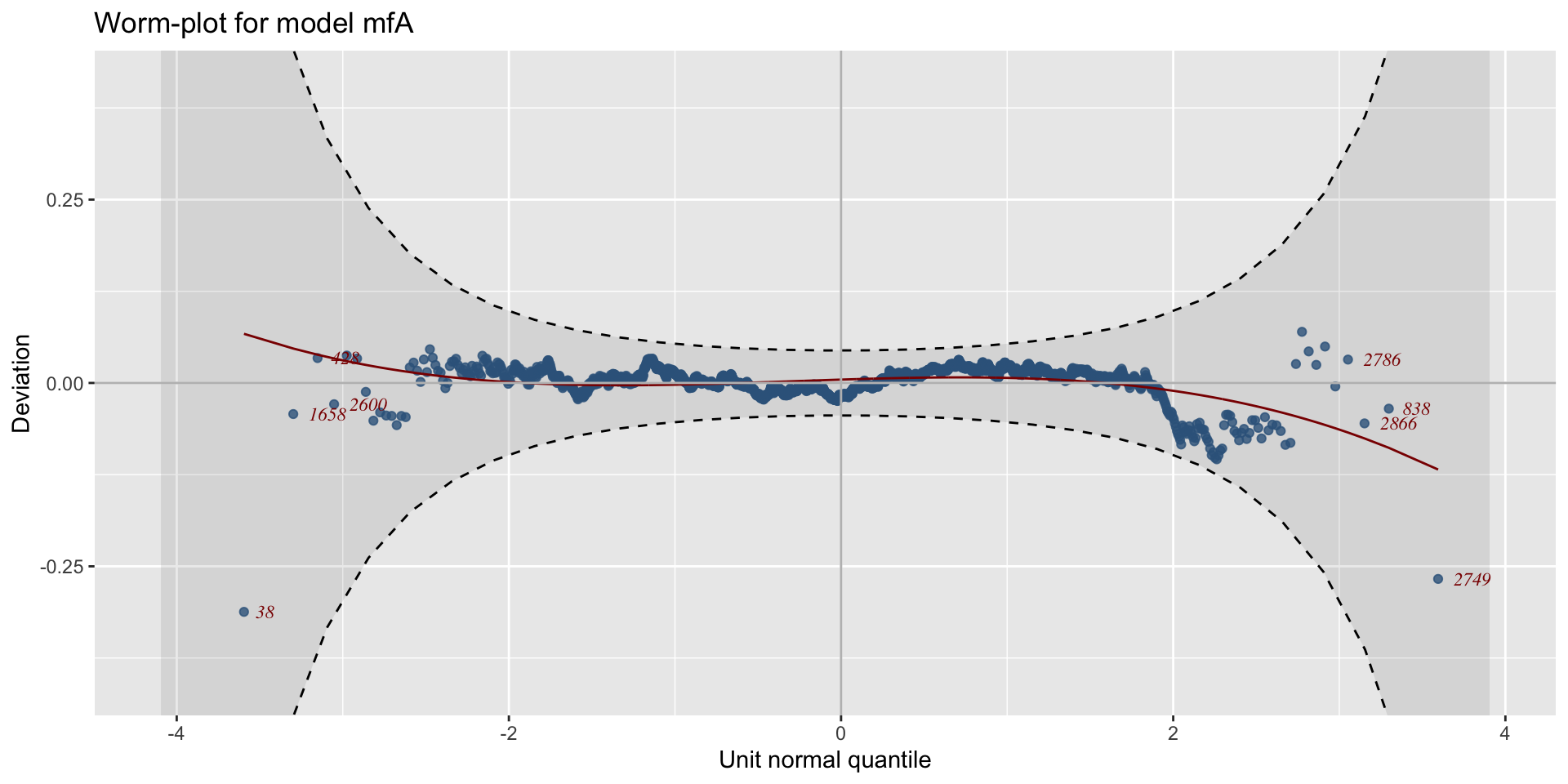
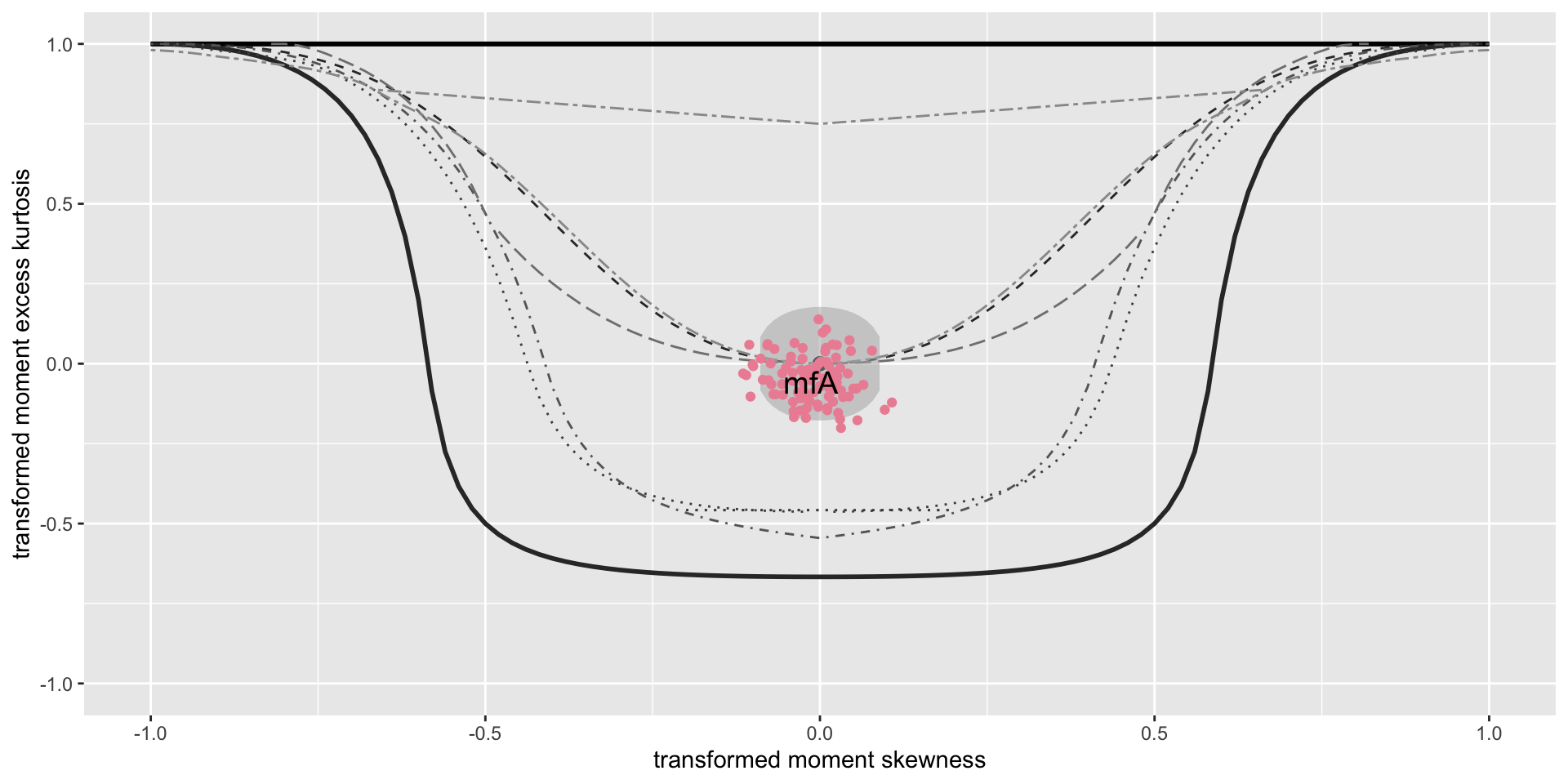
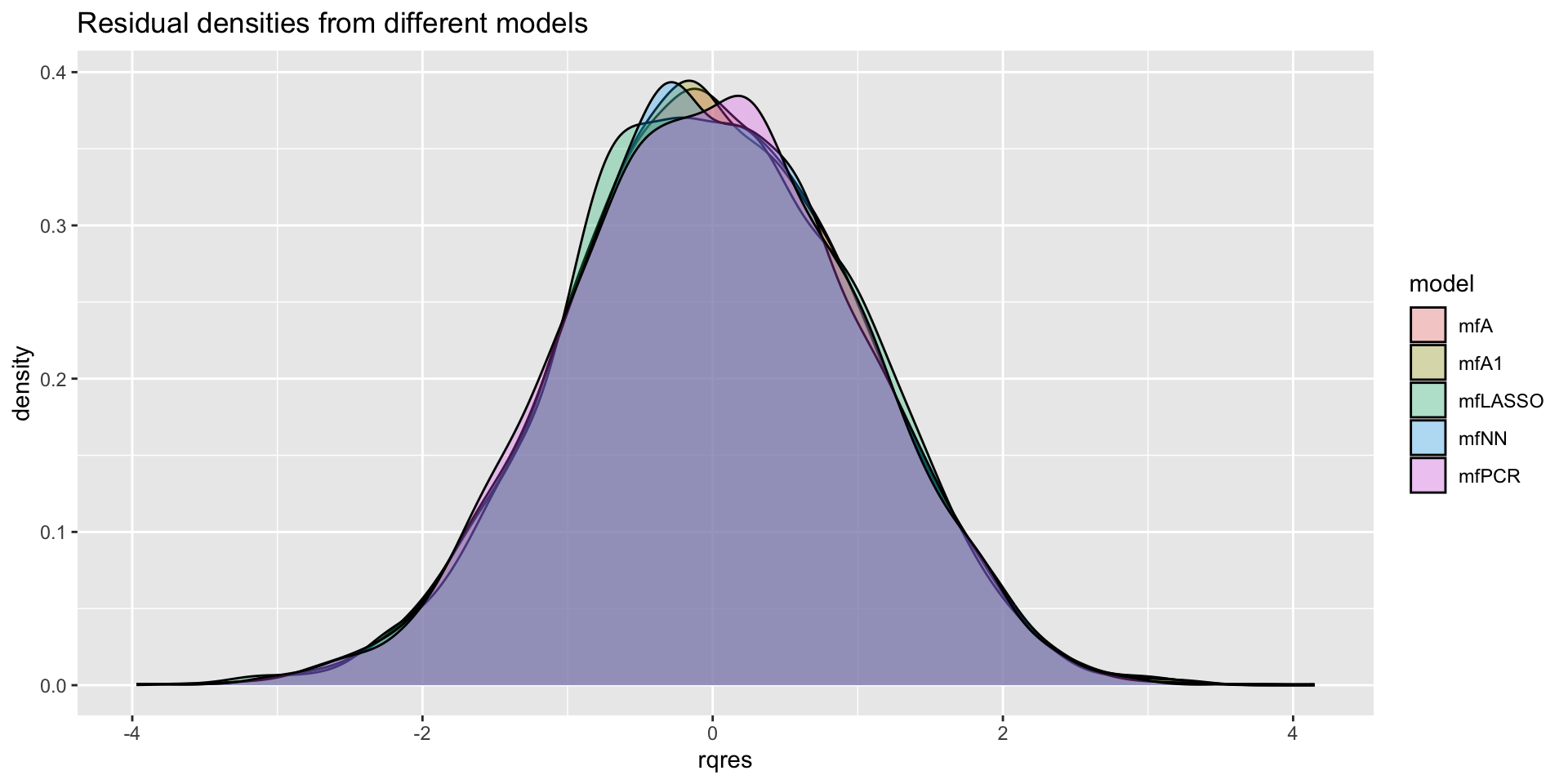
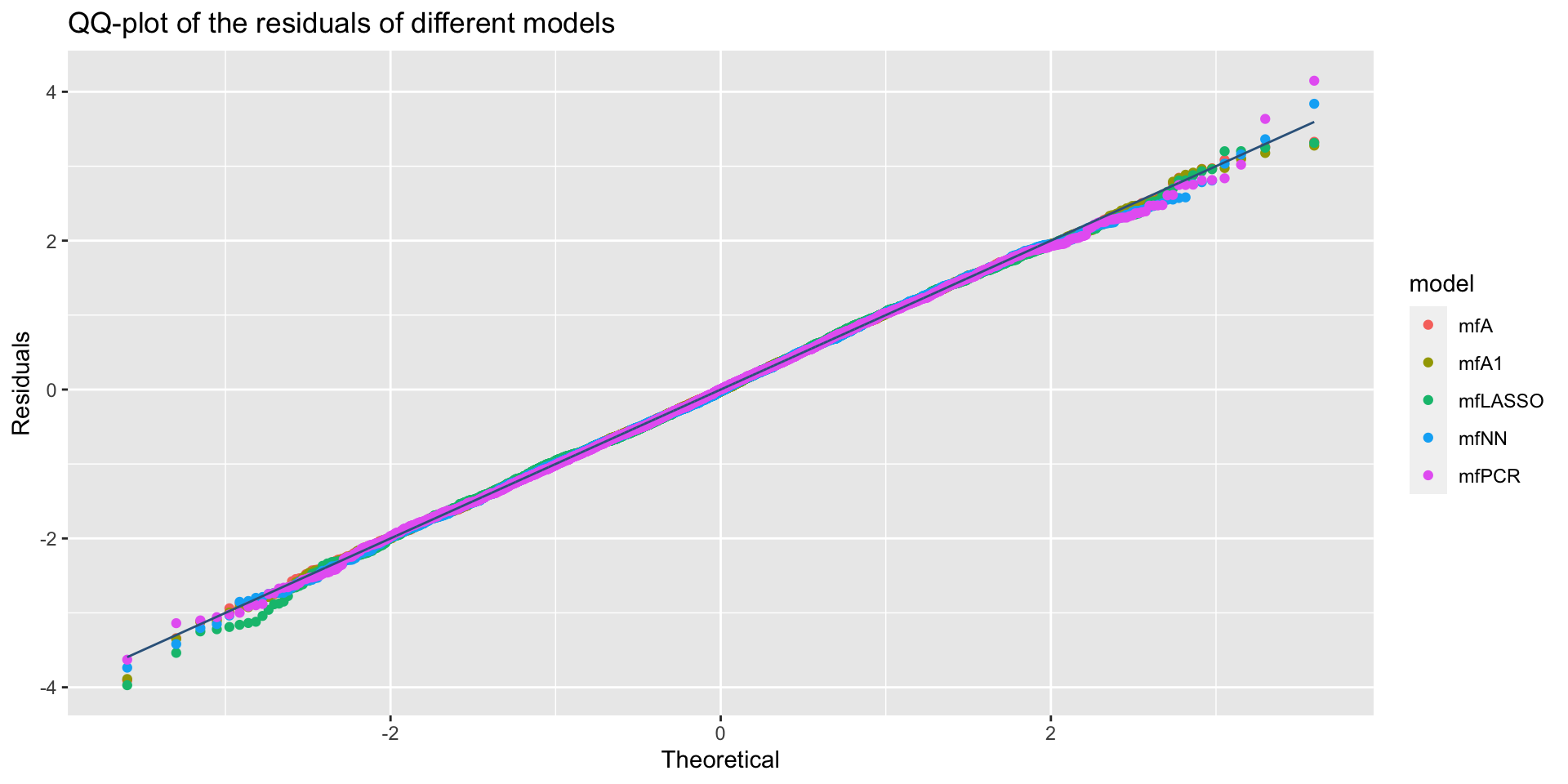
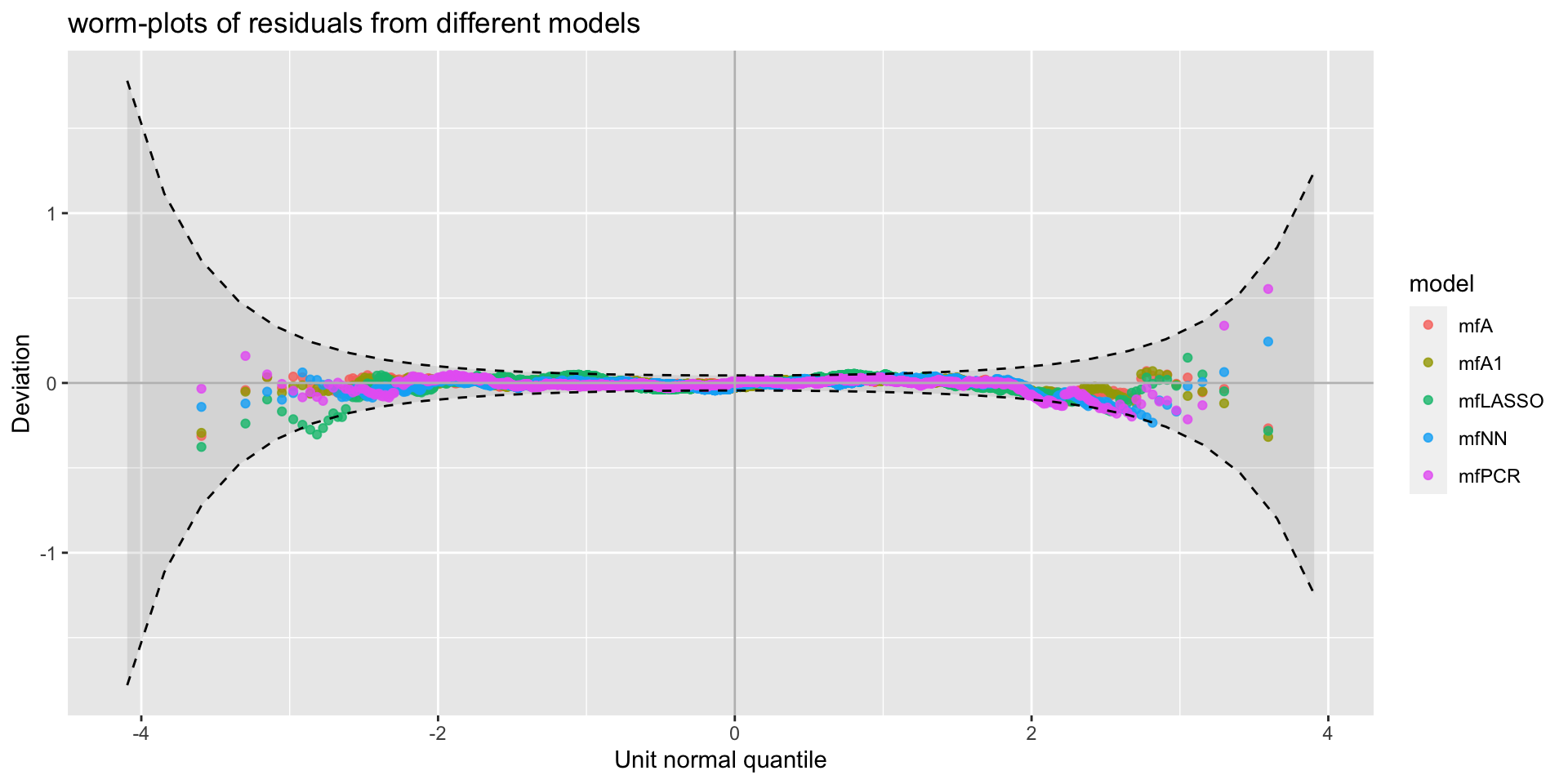
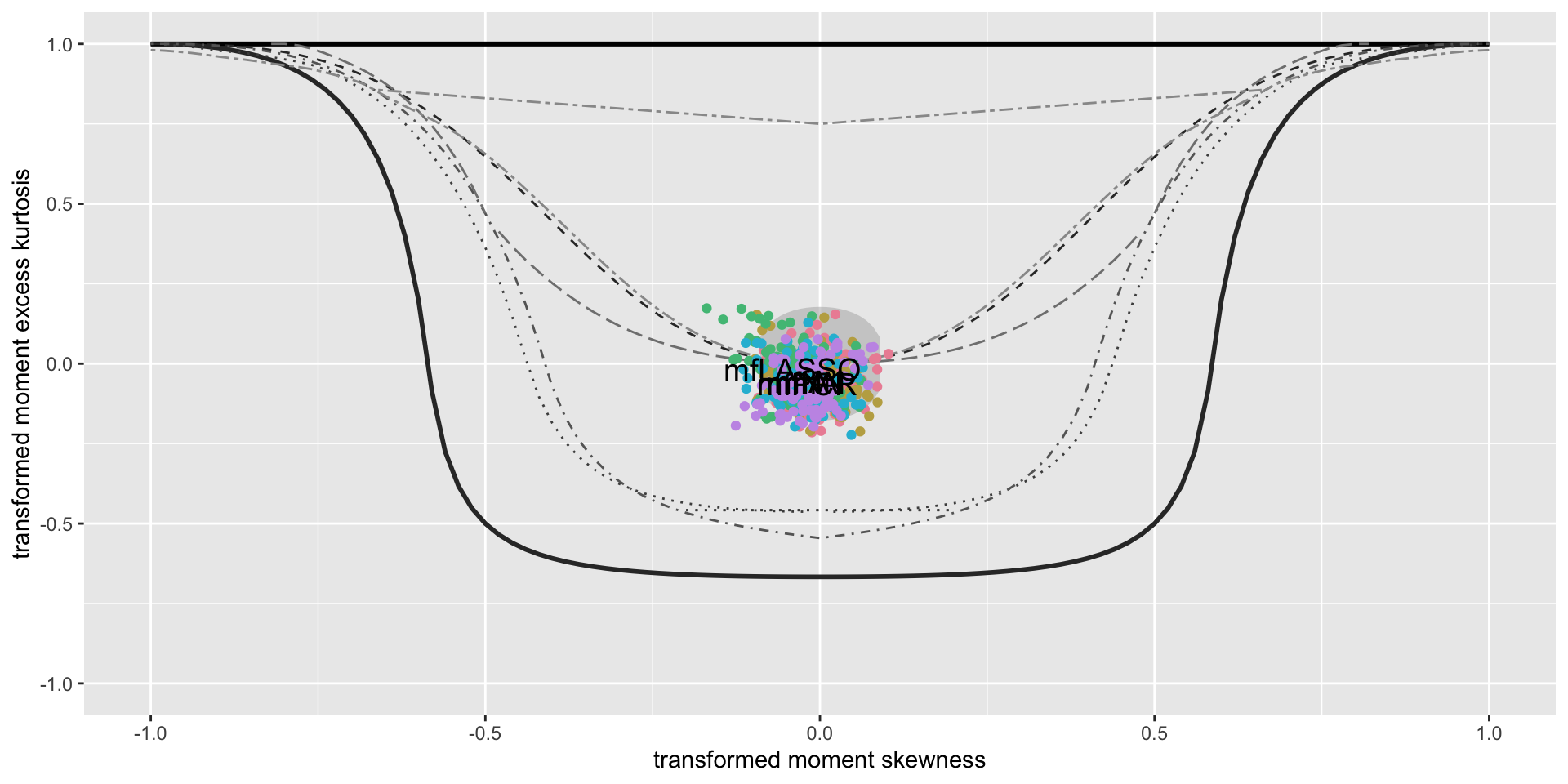
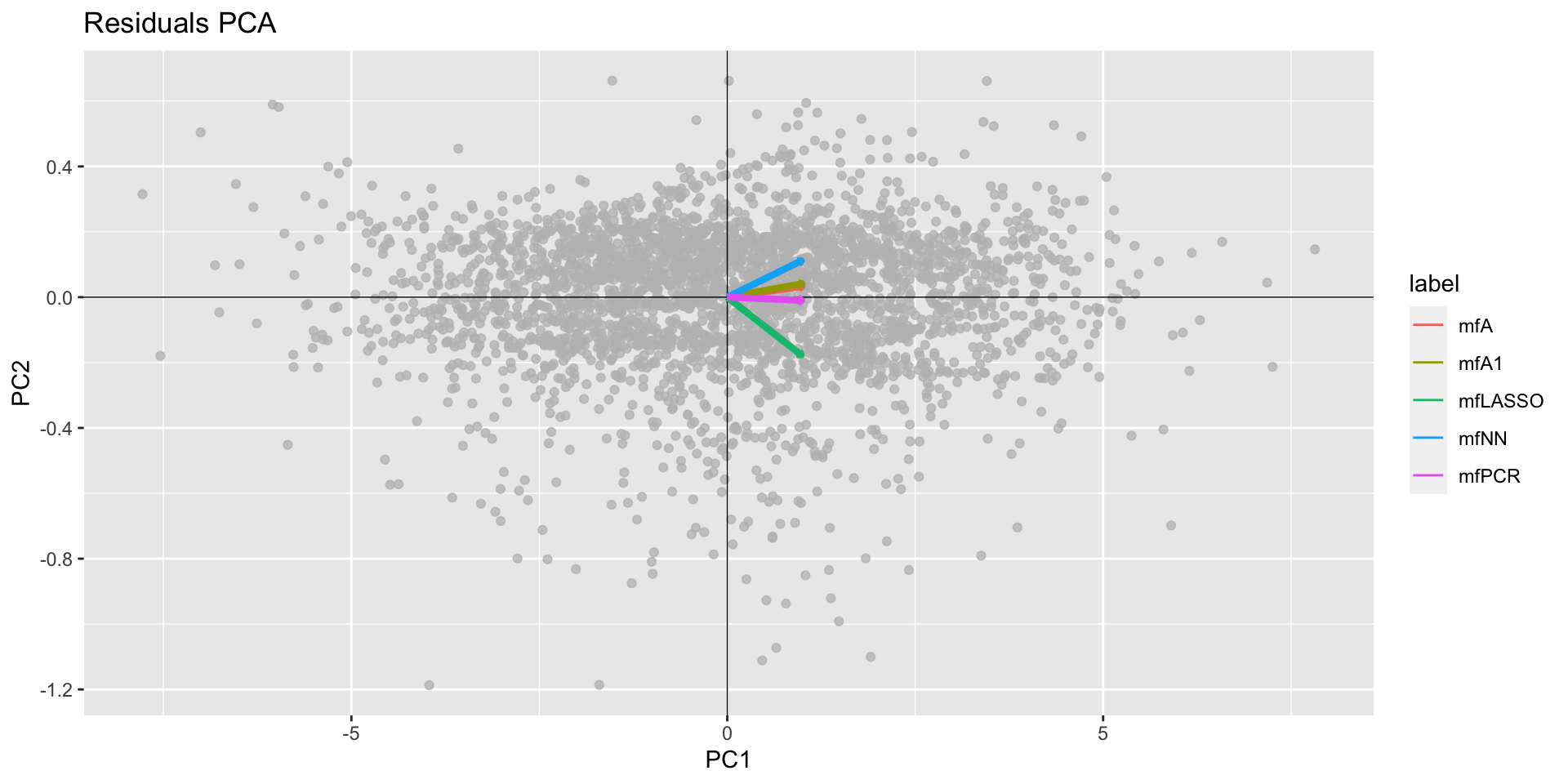
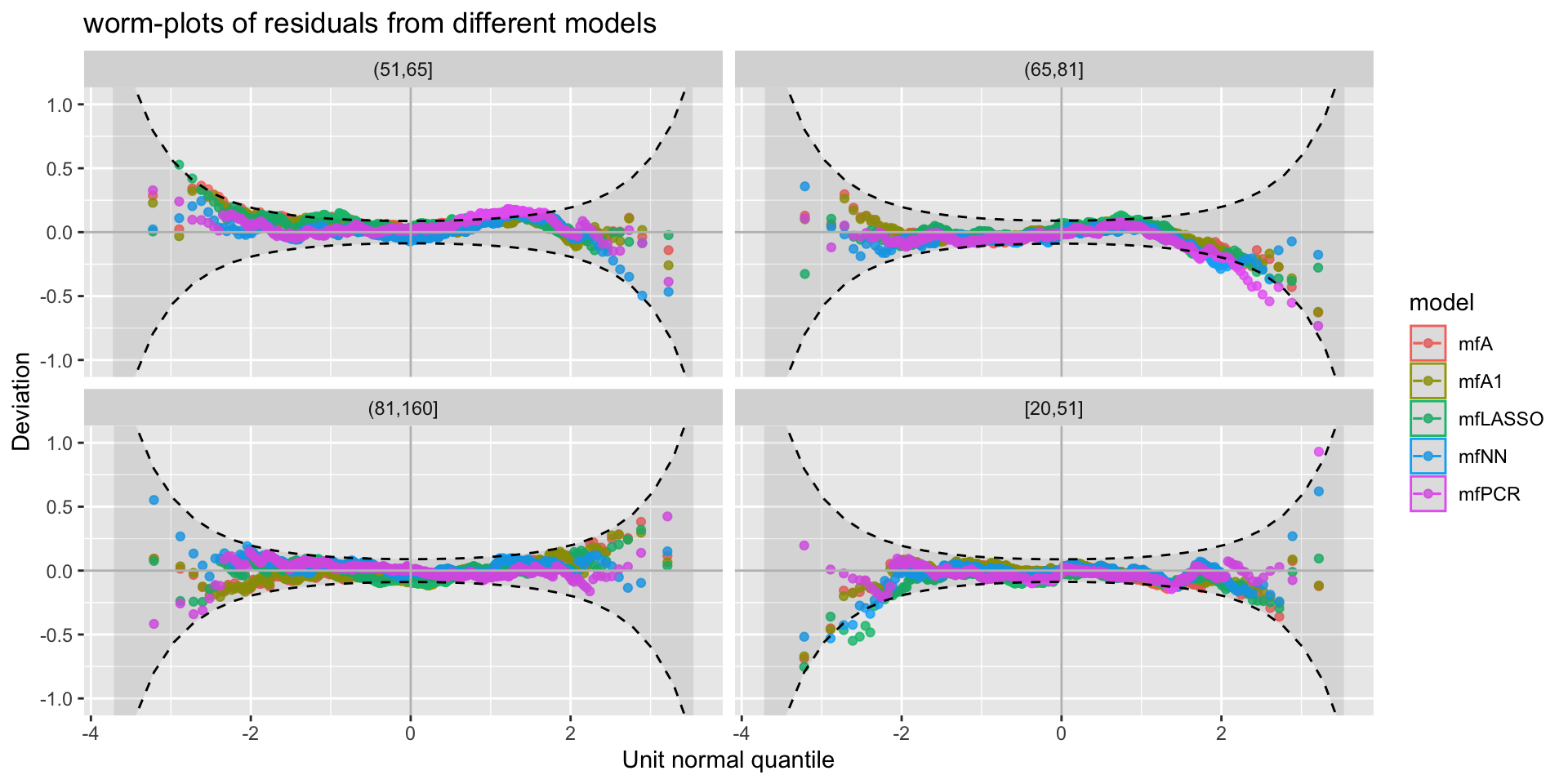
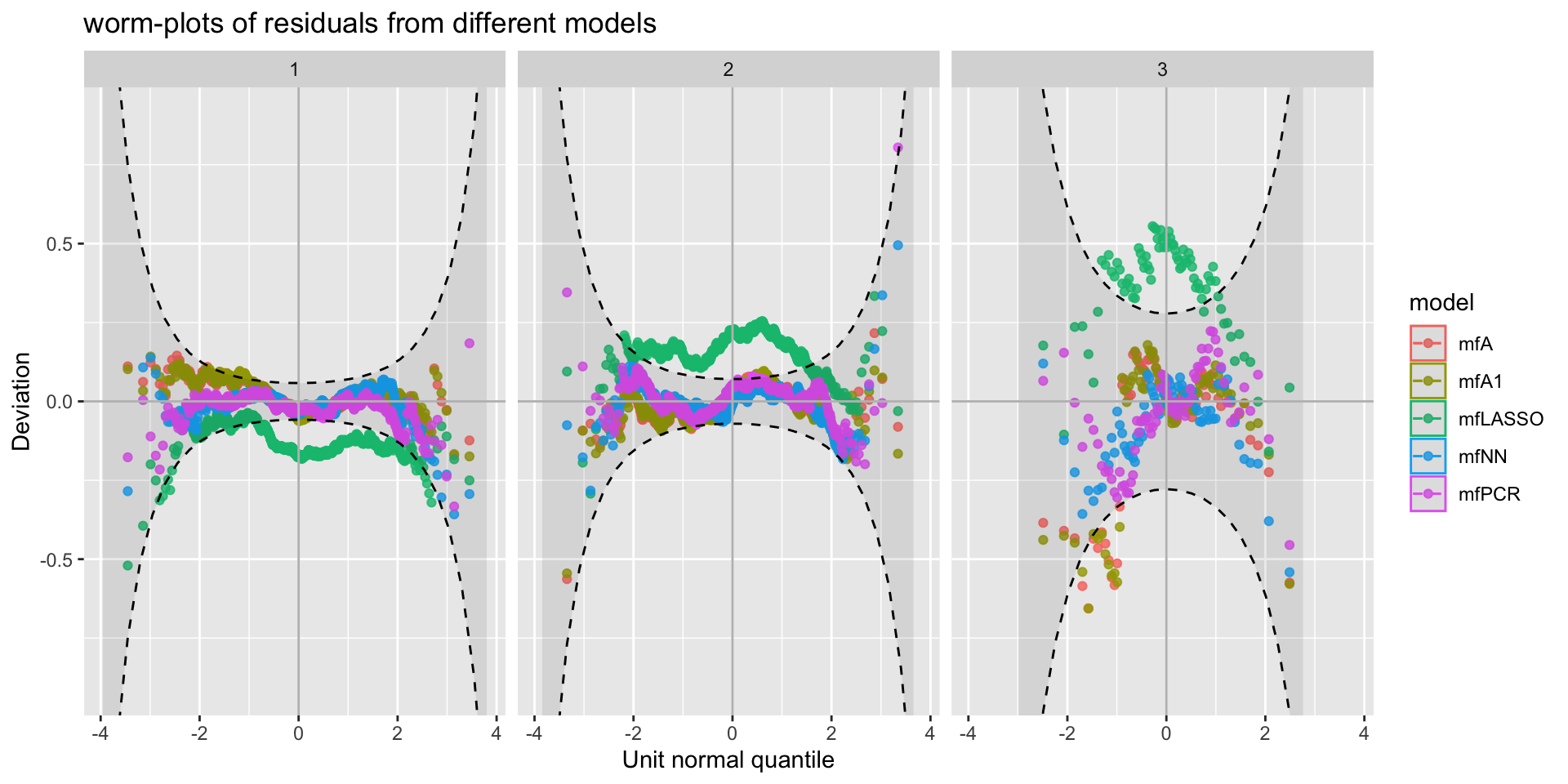
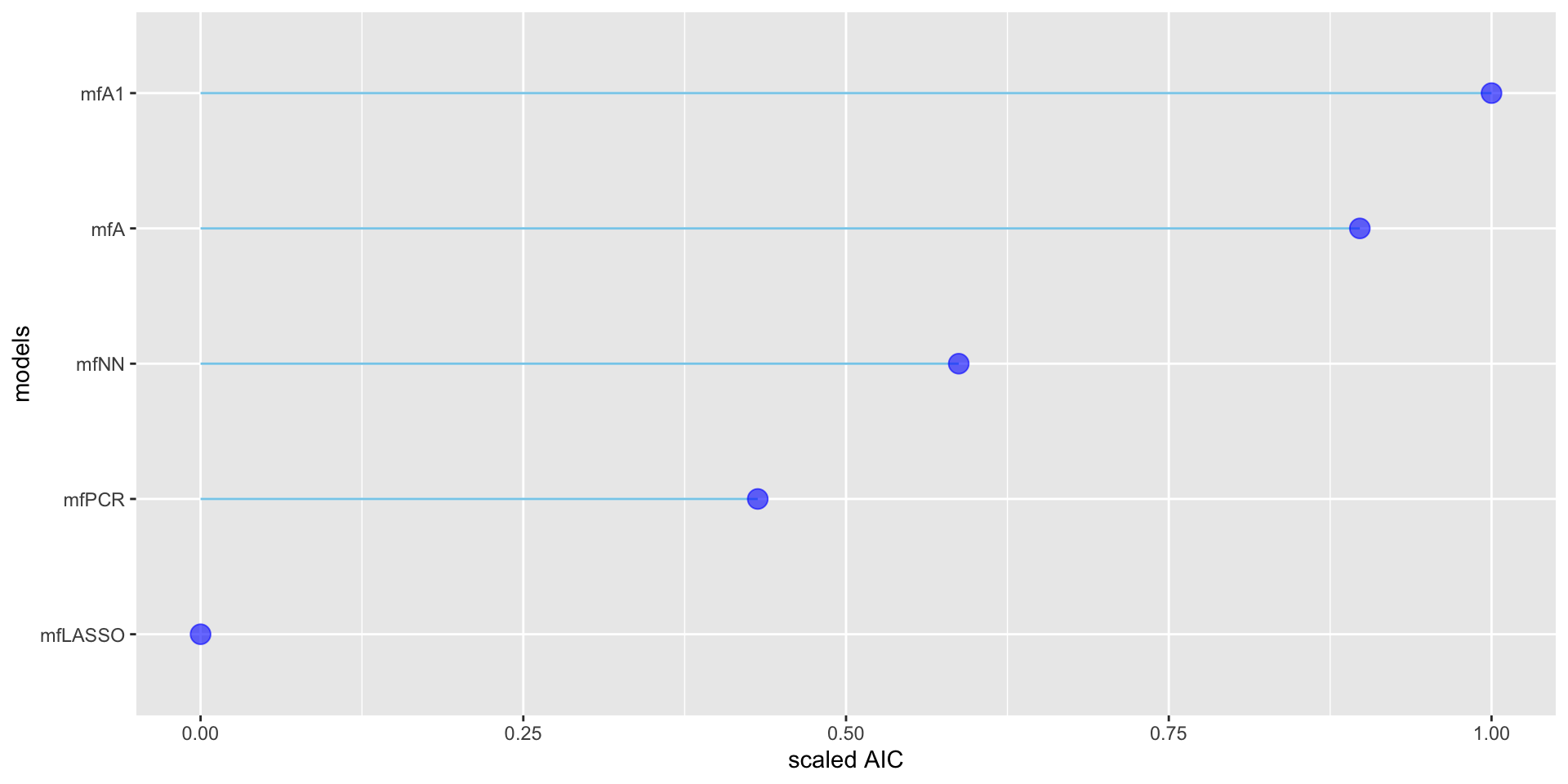
minimum GAIC(k= 2 ) model: mfA1 
minimum GAIC(k= 3.84 ) model: mfA1 
minimum GAIC(k= 8.03 ) model: mfA 

	df	k=2	k=3.84	k=8.03
mfA	23	38169.3	38211.6	38308.0
mfA1	27	38156.1	38206.0	38319.8
mfLASSO	23	38285.4	38327.7	38424.1
mfNN	134	38209.4	38456.0	39017.5
mfPCR	68	38229.6	38354.7	38639.6

GAIC (continuous)

Figure 1: A lollipop plot of AIC of the fitted models.

prediction measures

• \[MAPE= \texttt{med} \left(\left|100 \left(\frac{\hat{\mu}_i(\textbf{x}_i^*)-y^*}{y^*}\right) \right|_{i=1,\ldots.n}\right)\]
• \[LS= \sum_{i=1}^{n^*} \log \left[y^*_i | \hat{\theta}_i \left(\textbf{x}_i^*\right) \right] \]
• \[CRPS = -\sum_{i=1}^{n} \int \left(F(y| \hat{\theta}_i \left(\textbf{x}_i^*\right) -\textbf{I}\left(y \ge y^*_i\right)\right)^2 dy,\]

prediction measures table

models	MAPE	TGD	CRPS
mfA	17.938	-6.194	71.018
mFA1	17.974	-6.192	70.964
mfNN	17.593	-8.175	NA
mLASSO	NA	NA	NA
mFPCR	NA	NA	NA

The results vary with different partitions of the data. Here we use the same partition for all models.

summary

• the GAIC is well established (the the df of freedon need to be known)

• the linear and additive model are good when there are not many explanatory variables (but somehow interaction has to be considered)

• more work has to be done to standardised all ML techniques so their partitioning of data are comparable to the conventional additive models

end

back to the index

The Books

Appendix

residuals against variables

go back to Section 4

(a) index

(b) mu

(c) median

(d) area

Figure 2: Residuals against variables of interest

density

go back to Section 4

(a) density

ECDF plots

go back to Section 4

(a) ecdf

(b) Own’s detrened plot

Figure 4: Plots of the ECDF of the residuals

QQ and worm plots

go back to Section 4

(a) QQ-plot

(b) worm-plot

Figure 5: QQ and worm plots of of the residuals

Bucket plots

go back to Section 4

(a) bucket

ACF ands PACF plots

go back to Section 4

(a) ACF

(b) PACF

Figure 7: ACF and PACF of the residuals

model density

go back to Section 5

(a) density

model qqplots

go back to Section 5

(a) QQ-plots

model worm-plots

go back to Section 5

(a) worm plots

model bucket plot

go back to Section 5

(a) bucket plot

model PC-plot

go back to Section 5

(a) PC plot

model wp wrap

go back to Section 5

Figure 13: Worm plots for different fitted models at different values of the continuous variable area

model wp wrap (continue)

go back to Section 5

Figure 14: Worm plots for different fitted models at different levels of the factor location