Fitting models

Mikis Stasinopoulos
Bob Rigby
Fernanda De Bastiani
Gillian Heller
Niki Umlauf

Introduction

questions

  • do my data support a GAMLSS model?

  • do I need GAMLSS to answer my questions?

  • size of the data

  • questions of interest

this talk

  • the basic GAMLSS algorithm
  • different statistical approaches for fitting a GAMLSS model
  • different machine learning techniques for fitting a GAMLSS model.

Algorithms

GAMLSS

\[\begin{split} y_i & \stackrel{\small{ind}}{\sim }& {D}( \theta_{1i}, \ldots, \theta_{ki}) \nonumber \\ g(\theta_{1i}) &=& b_{10} + s_1({x}_{1i}) + \ldots, s_p({x}_{pi}) \nonumber\\ \ldots &=& \ldots \nonumber\\ g({\theta}_{ki}) &=& b_0 + s_1({x}_{1i}) + \ldots, s_p({x}_{pi}) \end{split} \qquad(1)\]

GAMLSS + ML

\[\begin{split} y_i & \stackrel{\small{ind}}{\sim }& {D}( \theta_{1i}, \ldots, \theta_{ki}) \nonumber \\ g({\theta}_{1i}) &=& {ML}_1({x}_{1i},{x}_{2i}, \ldots, {x}_{pi}) \nonumber \\ \ldots &=& \ldots \nonumber\\ g({\theta}_{ki}) &=& {ML}_1({x}_{1i},{x}_{2i}, \ldots, {x}_{pi}) \end{split} \qquad(2)\]

Parameters for Estimation

  • distribution parameters

  • coefficient parameters

      - **coefficients**

  - **random effects**

  • hyper-parameters

flowchart

flowchart LR
  A[GAMLSS] --> L[Parametric]
  A --> N[Smooth]
  L --> B(Likelihood)
  L --> D(Bayesian)
  L --> E(Boosting)
  N --> C(Penalised Likelihood)
  N --> D(Bayesian)
  N --> E(Boosting)
  B --> G[beta's]
  C --> F[beta's, gamma's, & lambda's]
  E --> F
  D --> F
  D --> G
  E --> G
Figure 1: Different ways to estimate the parameters in a GAMLSS model.

The Basic Algorithm for GAMLSS

  • For specified distribution family, data and machine learning (ML) model.

Initialize: set starting values for all distribution parameters \((\hat{\boldsymbol{\mu}}^{(0)}, \hat{\boldsymbol{\sigma}}^{(0)}, \hat{\boldsymbol{\nu}}^{(0)}, \hat{\boldsymbol{\tau}}^{(0)} )\).

For i in \(1,2,\ldots\)

  • fix \(\hat{\boldsymbol{\sigma}}^{(i-1)}\),\(\hat{\boldsymbol{\nu}}^{(i-1)}\), and \(\hat{\boldsymbol{\tau}}^{(i-1)}\) and fit a ML model to iterative response \(\textbf{y}_{\mu}\) using iterative weights \(\textbf{w}_{\mu}\) to obtain the new \(\hat{\boldsymbol{\mu}}^{(i)}\)

  • fix \(\hat{\boldsymbol{\mu}}^{(i)}\),\(\hat{\boldsymbol{\nu}}^{(i-1)}\), and \(\hat{\boldsymbol{\tau}}^{(i-1)}\) and fit a ML model to iterative response \(\textbf{y}_{\sigma}\) using iterative weights \(\textbf{w}_{\sigma}\) to obtain the new \(\hat{\boldsymbol{\sigma}}^{(i)}\)

  • fix \(\hat{\boldsymbol{\mu}}^{(i)}\),\(\hat{\boldsymbol{\sigma}}^{(i)}\), and \(\hat{\boldsymbol{\tau}}^{(i-1)}\) and fit a ML model to iterative response \(\textbf{y}_{\nu}\) using iterative weights \(\textbf{w}_{\nu}\) to obtain the new \(\hat{\boldsymbol{\nu}}^{(i)}\)

  • fix \(\hat{\boldsymbol{\mu}}^{(i)}\),\(\hat{\boldsymbol{\sigma}}^{(i)}\), and \(\hat{\boldsymbol{\nu}}^{(i)}\) and fit a ML model to iterative response \(\textbf{y}_{\tau}\) using iterative weights \(\textbf{w}_{\tau}\) to obtain the new \(\hat{\boldsymbol{\nu}}^{(i)}\)

  • check if the global deviance, \(-2(\textit{log-likelihood})\) does not change repeat otherwise exit

Important

  • assumed distribution (the log-likelihood is needed and the first and second derivatives)

  • hierarchy of the paramerers (i.e. a good location model is required before model the scale)

  • orthogonality of the parameters (leads to better convergence)

Checking orthogonality

  • Specify a distribution family, and select values for all the parameters.

  • generate a sample of of N observations (default \(N=10000\))

  • fit the distribution to the generated sample.

  • display the correlation coefficients of the estimated predictors, \(\eta_{\theta}\).

Checking orthogonality (con.)

source("~/Dropbox/GAMLSS-development/ggplot/family_cor.R")
library(gamlss)
library(ggplot2)
family_cor("BCTo", mu=1, sigma=0.11, nu=1, tau=5, no.sim=10000)

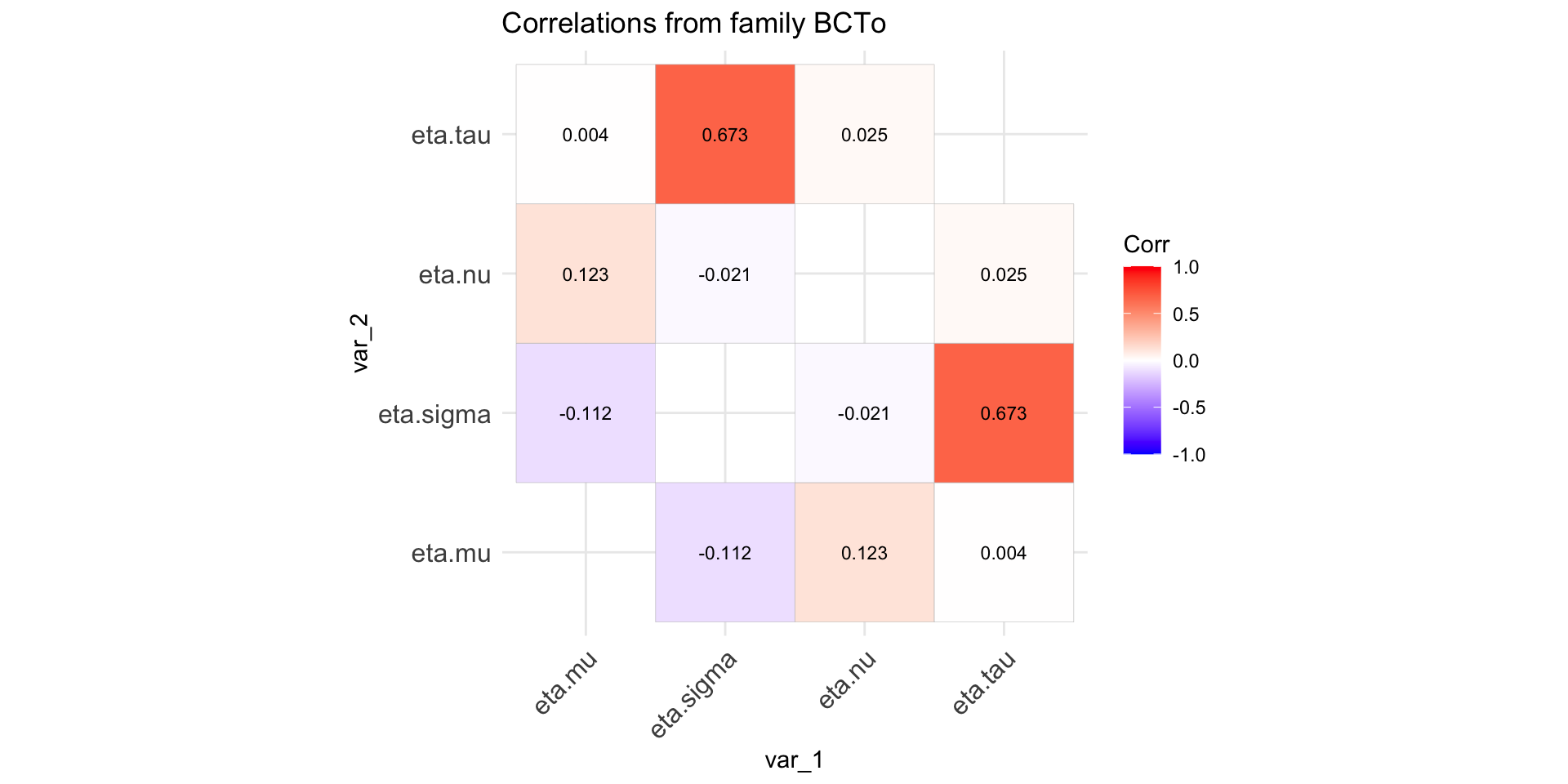
Figure 2: Paramater orthogonality for BCTo distribution

Machine Learning Models

properties

  • are the standard errors available?

  • do the x’s need standardization.

  • about the algorithm

     - stability
 - speed 
 - convergence

  • nonlinear terms

  • interactions

  • dataset type

  • is the selection of x’s automatic?

  • interpretation

Linear Models

mlinear <- gamlss2(rent~area+poly(yearc,2)+location+bath+kitchen+
              cheating|area+yearc+location+bath+kitchen+cheating, 
              family=BCTo, trace=FALSE, data=da)
summary(mlinear)

Linear Models

Call:
gamlss2(formula = rent ~ area + poly(yearc, 2) + location + bath + 
    kitchen + cheating | area + yearc + location + bath + kitchen + 
    cheating, data = da, family = BCTo, ... = pairlist(trace = FALSE))
---
Family: BCTo 
Link function: mu = log, sigma = log, nu = identity, tau = log
*--------
Parameter: mu 
---
Coefficients:
                 Estimate Std. Error t value Pr(>|t|)    
(Intercept)     5.0132864  0.0275445 182.007  < 2e-16 ***
area            0.0106293  0.0002329  45.640  < 2e-16 ***
location2       0.0878750  0.0104118   8.440  < 2e-16 ***
location3       0.1983303  0.0383017   5.178 2.39e-07 ***
bath1           0.0415152  0.0206509   2.010   0.0445 *  
kitchen1        0.1129557  0.0236130   4.784 1.80e-06 ***
cheating1       0.3304758  0.0240475  13.743  < 2e-16 ***
poly(yearc, 2)1 5.0471663  0.3301520  15.287  < 2e-16 ***
poly(yearc, 2)2 3.3575299  0.2751069  12.204  < 2e-16 ***
*--------
Parameter: sigma 
---
Coefficients:
              Estimate Std. Error   t value Pr(>|t|)    
(Intercept)  1.047e+01  6.245e-02   167.650  < 2e-16 ***
area         1.218e-03  6.099e-04     1.996   0.0460 *  
yearc       -5.972e-03  8.078e-07 -7392.764  < 2e-16 ***
location2    5.971e-02  2.911e-02     2.051   0.0403 *  
location3    2.176e-01  9.224e-02     2.359   0.0184 *  
bath1        5.069e-03  5.966e-02     0.085   0.9323    
kitchen1     3.750e-02  7.106e-02     0.528   0.5977    
cheating1   -2.431e-01  4.766e-02    -5.100  3.6e-07 ***
*--------
Parameter: nu 
---
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.65342    0.05454   11.98   <2e-16 ***
*--------
Parameter: tau 
---
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  3.18974    0.01758   181.4   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
*--------
n = 3082 df =  19 res.df =  3063
Deviance = 38254.617 Null Dev. Red. = 5.95%
AIC = 38292.617 elapsed =  0.32sec

Additive Models

madditive <- gamlss2(rent~s(area)+s(yearc)+location+bath+kitchen+
                cheating|s(area)+s(yearc)+location+bath+kitchen+cheating, 
              family=BCTo, data=da, trace=F)
GAIC(mlinear, madditive)
               AIC      df
madditive 38196.95 32.2364
mlinear   38292.62 19.0000

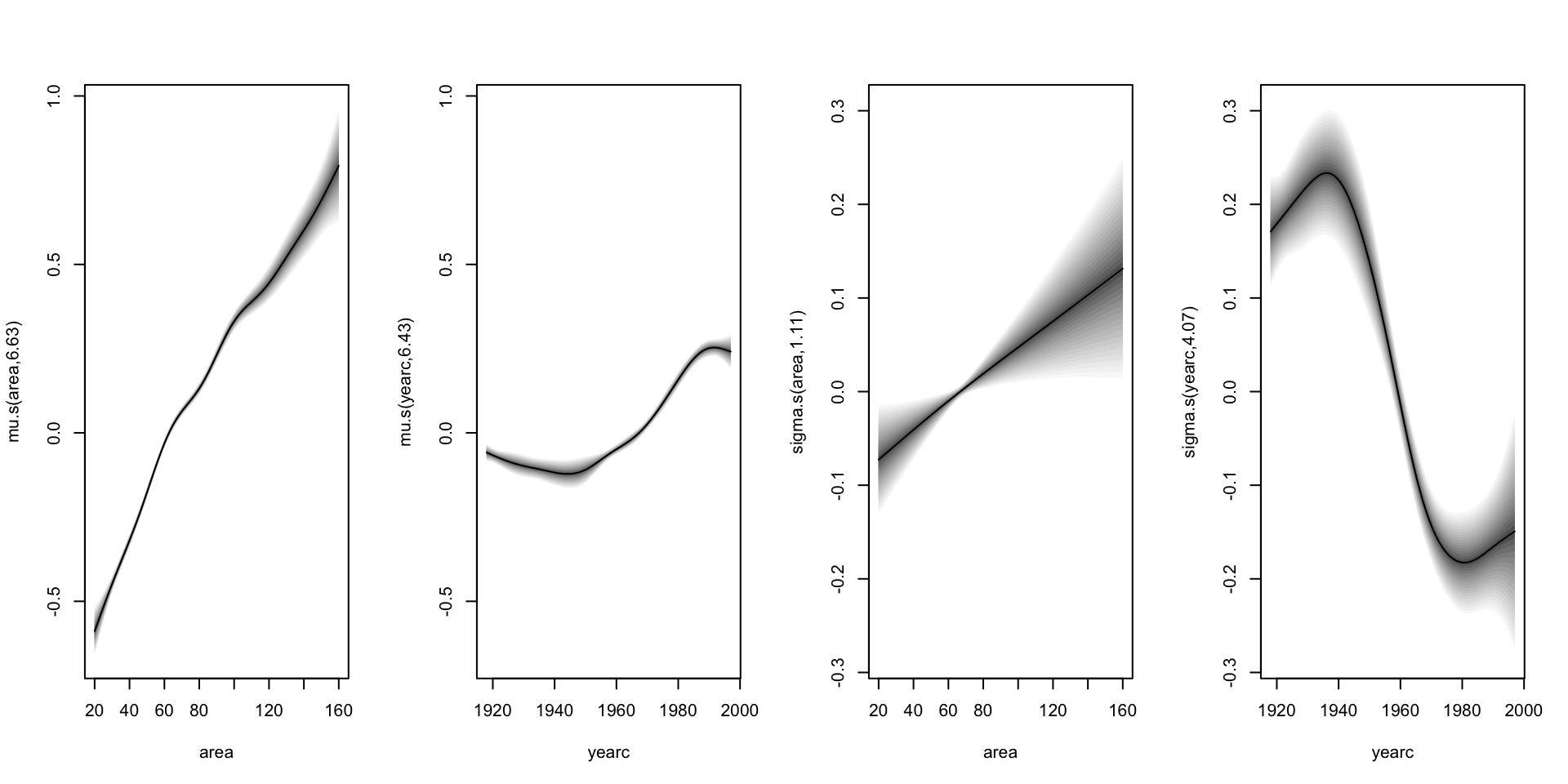
Additive Models (con.)

summary(madditive)
Call:
gamlss2(formula = rent ~ s(area) + s(yearc) + location + bath + 
    kitchen + cheating | s(area) + s(yearc) + location + bath + 
    kitchen + cheating, data = da, family = BCTo, ... = pairlist(trace = F))
---
Family: BCTo 
Link function: mu = log, sigma = log, nu = identity, tau = log
*--------
Parameter: mu 
---
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  5.71524    0.02082 274.541  < 2e-16 ***
location2    0.08808    0.01102   7.994 1.83e-15 ***
location3    0.20998    0.04965   4.229 2.41e-05 ***
bath1        0.05792    0.04280   1.353  0.17605    
kitchen1     0.10859    0.03642   2.982  0.00289 ** 
cheating1    0.34594    0.02021  17.114  < 2e-16 ***
---
Smooth terms:
    s(area) s(yearc)
edf  6.6271   6.4275
*--------
Parameter: sigma 
---
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.15569    0.03695 -31.277  < 2e-16 ***
location2    0.05293    0.02264   2.338   0.0195 *  
location3    0.21218    0.08616   2.463   0.0138 *  
bath1        0.03440    0.08318   0.414   0.6792    
kitchen1     0.01861    0.07591   0.245   0.8063    
cheating1   -0.23431    0.03754  -6.242 4.91e-10 ***
---
Smooth terms:
    s(area) s(yearc)
edf  1.1077   4.0742
*--------
Parameter: nu 
---
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.69275    0.04548   15.23   <2e-16 ***
*--------
Parameter: tau 
---
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  3.26960    0.07549   43.31   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
*--------
n = 3082 df =  32.24 res.df =  3049.76
Deviance = 38132.48 Null Dev. Red. = 6.25%
AIC = 38196.9528 elapsed =  0.47sec

Additive Models (con.)

plot(madditive)

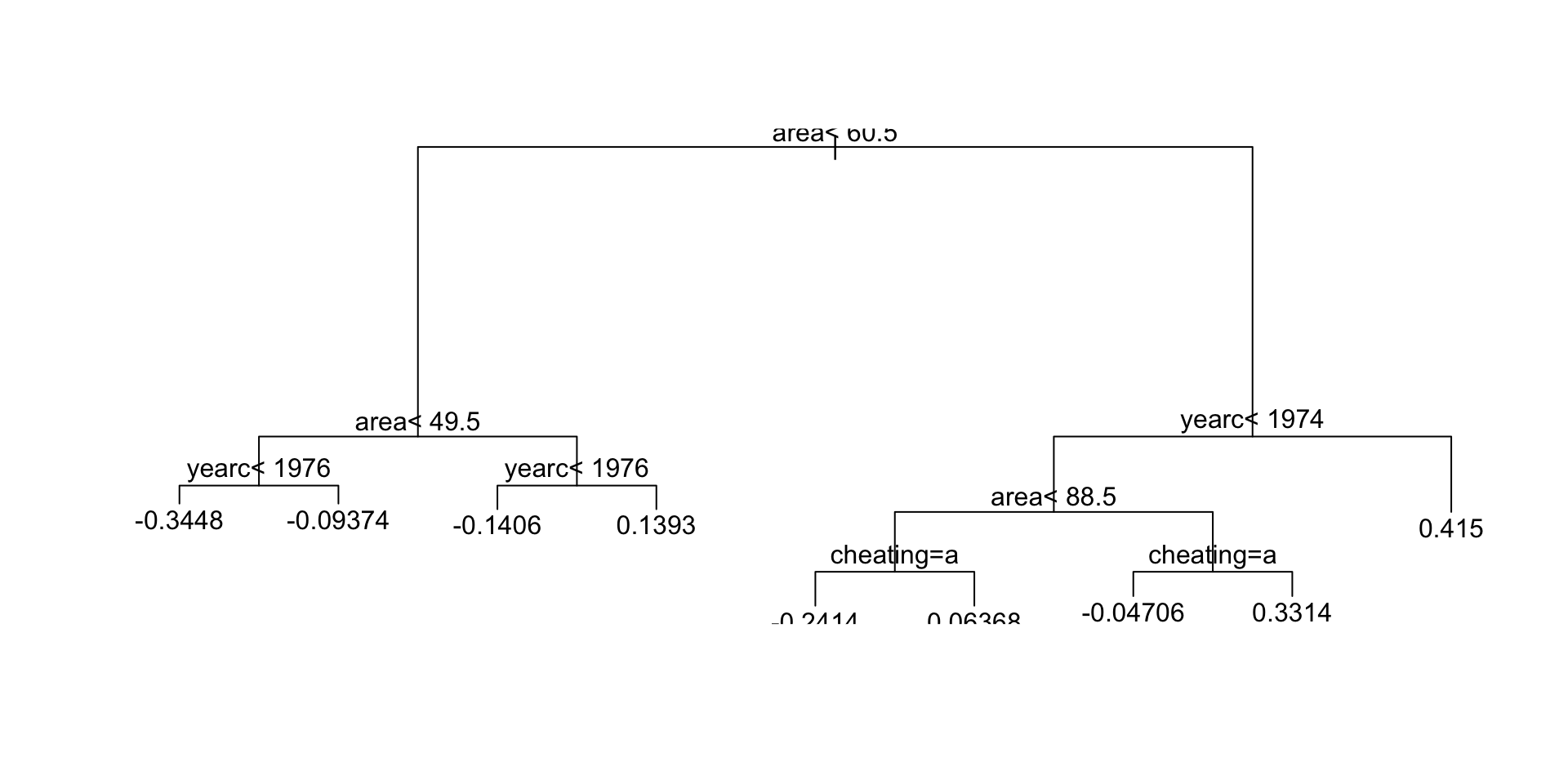
Regression Trees

source("~/Dropbox/GAMLSS-development/nnet/reg.tree.R")
mregtree <- gamlss2(rent~tree(~area+yearc+location+bath+kitchen+cheating)|
                       tree(~area+yearc+location+bath+kitchen+cheating),
                  family=BCTo, data=da, trace=FALSE) 

GAIC(mlinear, madditive, mregtree)
               AIC      df
madditive 38196.95 32.2364
mlinear   38292.62 19.0000
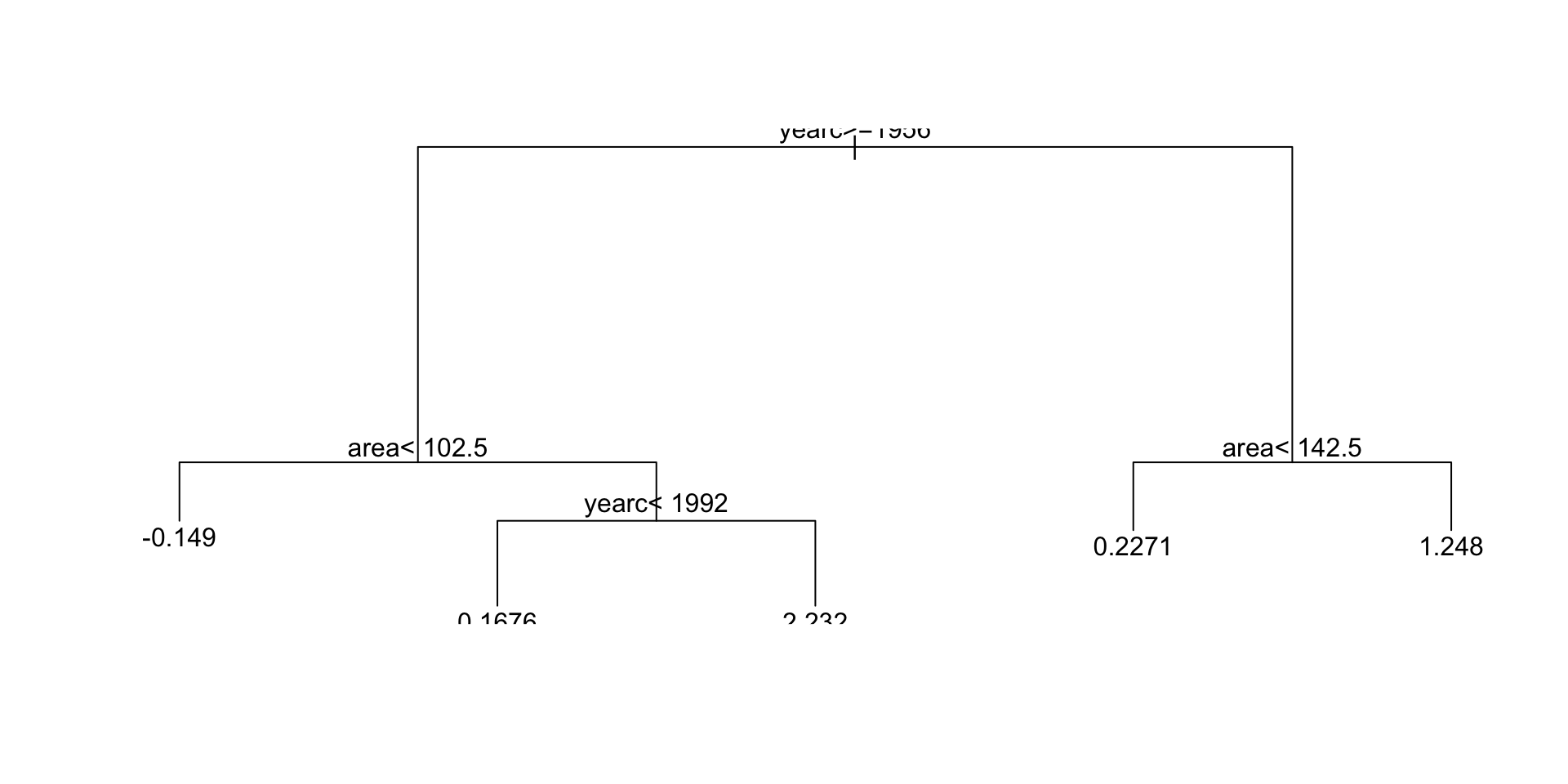
mregtree  38754.64 30.0000

Regression Trees (con.)

pp<- specials(mregtree, model = "mu", elements = "model")
plot(pp)
text(pp)

Regression Trees (continue)

pp<-specials(mregtree, model = "sigma", elements = "model")
plot(pp)
text(pp)

Neural Networks (fit)

f <- rent ~ n(~area+yearc+location+bath+kitchen, size=10)|      n(~area+yearc+location+bath+kitchen, size=3)
mneural <- gamlss2(f,family=BCTo, data=da)
GAMLSS-RS iteration  1: Global Deviance = 38208.8675 eps = 0.289873     
GAMLSS-RS iteration  2: Global Deviance = 38178.0402 eps = 0.000806     
GAMLSS-RS iteration  3: Global Deviance = 38177.034 eps = 0.000026     
GAMLSS-RS iteration  4: Global Deviance = 38176.766 eps = 0.000007     
gamlss2::GAIC(mlinear, madditive, mneural, mregtree, k=2)
               AIC       df
madditive 38196.95  32.2364
mlinear   38292.62  19.0000
mneural   38396.77 110.0000
mregtree  38754.64  30.0000

Neural Networks (plot)

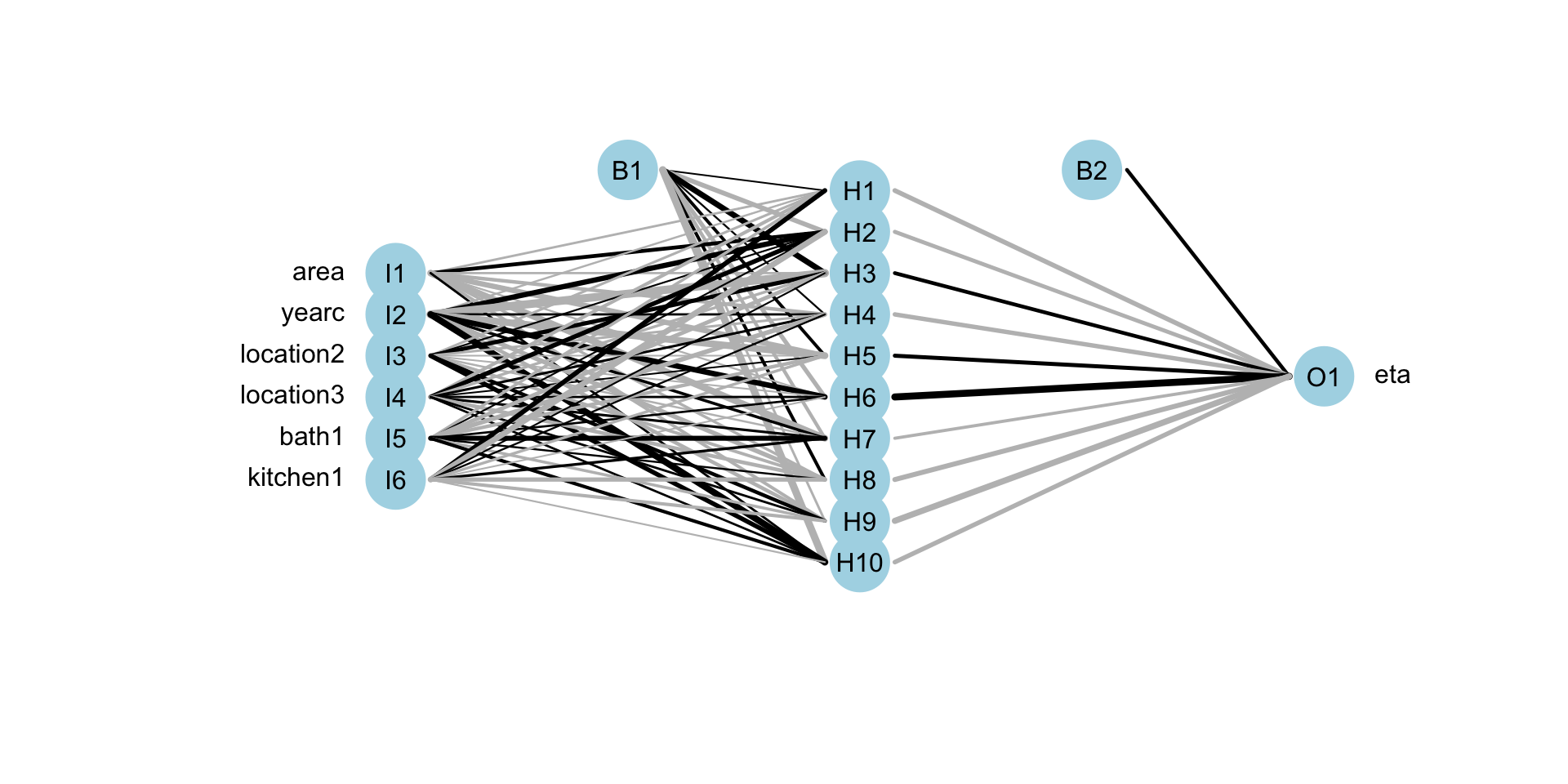
source("~/Dropbox/GAMLSS-development/nnet/plot_NN.R")
 plot(specials(mneural, model = "mu", elements = "model"))

Neural Networks (plot)

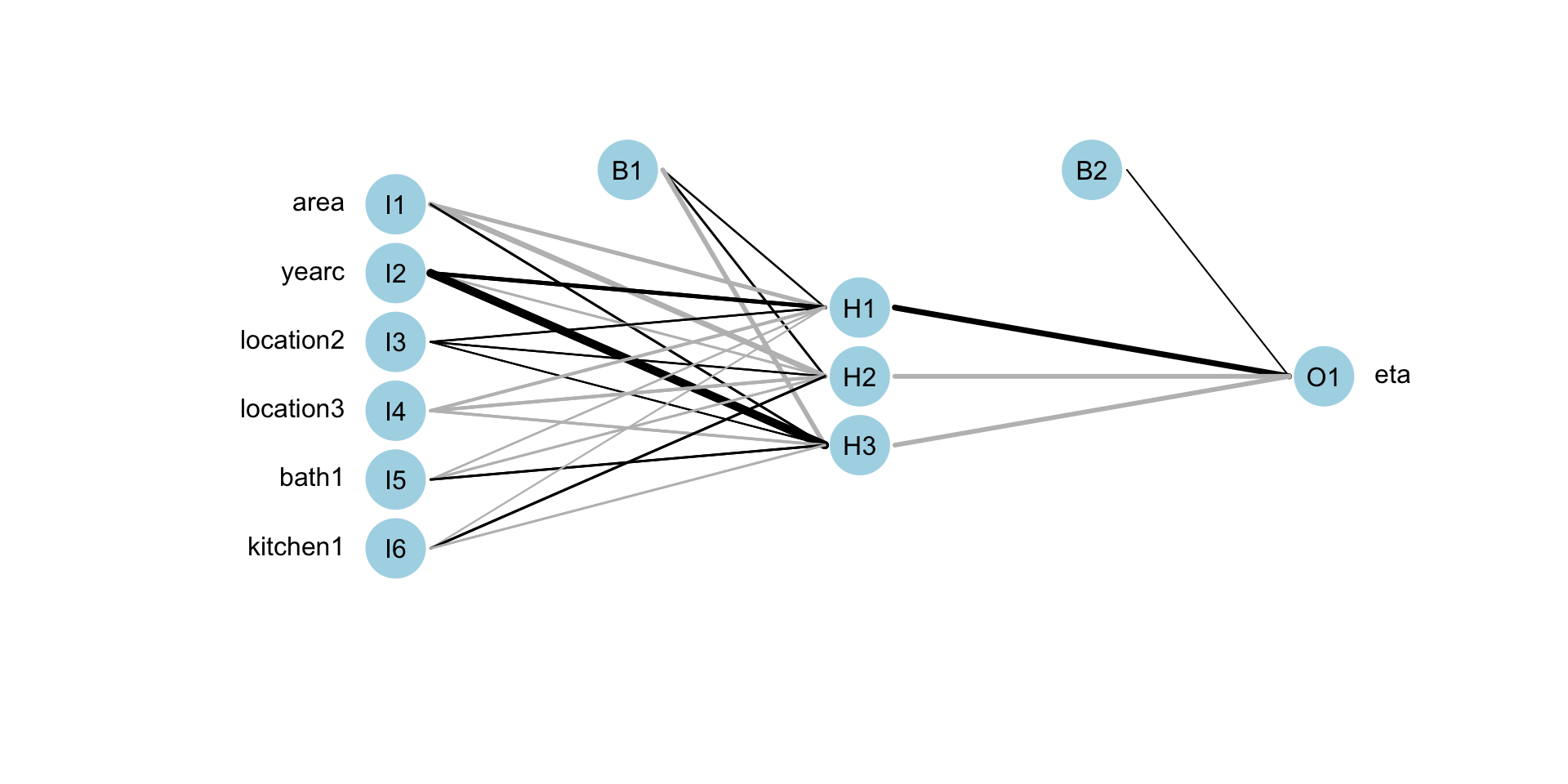
source("~/Dropbox/GAMLSS-development/nnet/plot_NN.R")
plot(specials(mneural, model = "sigma", elements = "model"))

random forest

f <- rent ~ cf(~area+yearc+location+bath+kitchen)|    cf(~area+yearc+location+bath+kitchen)
mcf <- gamlss2(f,family=BCTo, data=da)
GAMLSS-RS iteration  1: Global Deviance = 38465.948 eps = 0.285095     
GAMLSS-RS iteration  2: Global Deviance = 38295.835 eps = 0.004422     
GAMLSS-RS iteration  3: Global Deviance = 38289.9702 eps = 0.000153     
GAMLSS-RS iteration  4: Global Deviance = 38288.2421 eps = 0.000045     
GAMLSS-RS iteration  5: Global Deviance = 38287.9638 eps = 0.000007     
gamlss2::GAIC(mlinear, madditive, mneural, mregtree, mcf, k=2)
               AIC       df
madditive 38196.95  32.2364
mlinear   38292.62  19.0000
mneural   38396.77 110.0000
mcf       38695.96 204.0000
mregtree  38754.64  30.0000

LASSO-RIDGE

  • there is function ri() in gamlss using P-splines

  • there is also package gamlss.lasso for gamlss connecting with package glmnet

  • but LASSO is non implemented for gamlss2 yet

Principal Componet Regression

  • functions pc() and pcr() in gamlss.foreach package for gamlss

  • PCR is non implemented for gamlss2 yet

summary

Table 1: Summary of properties of the machine learning algorithms
ML Models coef. s.e. stand. of x’s algo. stab., speed, conv. non-linear terms inter- actions data type auto sele-ction interpre- tation
linear yes no yes, fast, v.good poly declare \(n>r\) no v. easy
additive no no yes, slow, good smooth declare \(n>r\) no easy
RT no no no, slow, bad trees auto \(n>r\)?? yes easy

summary (continue)

Table 2: Summary of properties of the machine learning algorithms
ML Models coef. s.e. stand. of x’s algo. stab., speed, conv. non-linear terms inter- actions data type auto sele-ction interpre- tation
NN no 0 to 1 no, \(\,\,\) ok, \(\,\,\) ok auto auto both? yes v. hard
RF no no no, slow, slow YES no both auto hard
LASSO no yes yes, fast, good poly declare both auto easy

summary (continue)

Table 3: Summary of properties of the machine learning algorithms
ML Models coef. s.e. stand. of x’s algo. stab., speed, conv. non-linear terms inter- actions data type auto sele-ction interpre- tation
Boost no no yes, fast, good smooth trees declare \(n<<r\) yes easy
MCMC yes no good, ok, \(\,\,\) ok smooth declare \(n>r\) no easy
PCR yes yes yes, fast, good poly declare both auto hard

end

back to the index

The Books

www.gamlss.com