Comparing Models

Mikis Stasinopoulos

Bob Rigby

Fernanda De Bastiani

Gillian Heller

Niki Umlauf

Introduction

• what to compare

  • distributions
  • x-variables

• how ro compare

  • graphical diagnostic tools;
  • model summary statistics

summary statistics

Data	Methods
all data	\(\chi^2\), GAIC
test data	LS, CRPS, MSE etc.
data partitioning
K-fold	LS, CRPS
bootstrap	LS, CRPS

Summary Comparison Statistics

• if no partition evaluation is done in the training dataset
  • Generalized AIC
    \[ GAIC = \hat{GD}+ k \times df \]
  • \(\chi^2\) test: likelihood ratio test for nested models \[LR= GD_1/ GD_0 \sim \chi^2(df0- df_1) \]

Note that degrees of freedom are required

Summary Comparison Statistics (con.)

• partition: evaluation is done on new data

  • Likelihod score (LS) \(\equiv\) Prediction Global Deviance (PGD)
  • Continuous Rank Probabily Score (CRPS)
  • Mean Absolute Prediction Error (MAPE)
  • e.t.c.

no partition

GAIC

models	df	AIC	\(\chi^2\)	BIC
mlinear	24	22808.89	22855.45	22953.69
madditive	29.24	22814.33	22871.07	22990.77
mfneural	160	22930.36	23240.76	23895.69
mregtree	30	38754.64	38812.84	38935.64
mcf	404	38754.64	24481.28	26134.99

GAIC (continuous)

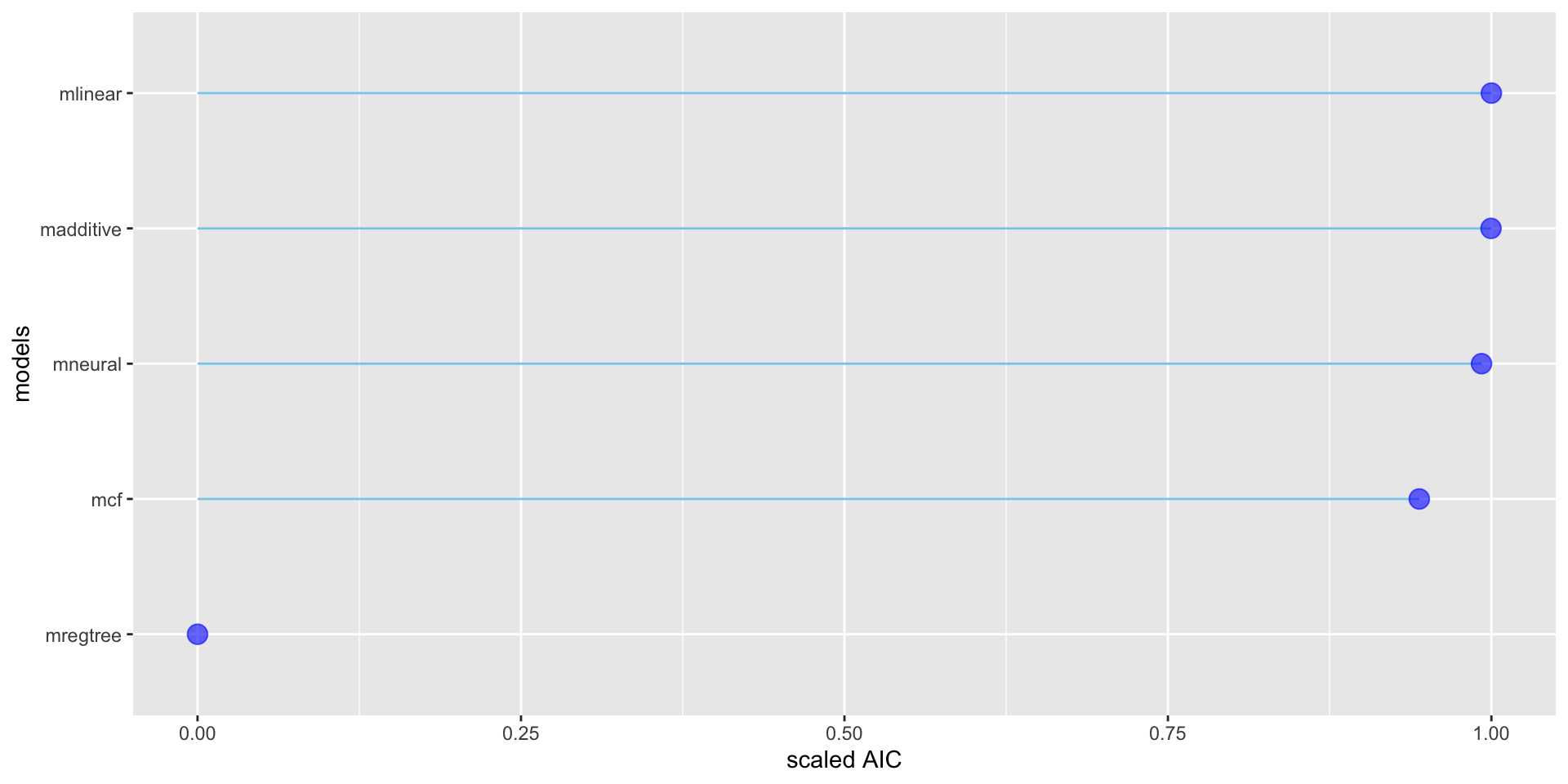
Figure 1: A lollipop plot of AIC of the fitted models.

partition

prediction measures

• \[LS= \sum_{i=1}^{n^*} \log \left[y^*_i | \hat{\theta}_i \left(\textbf{x}_i^*\right) \right] \]
• \[CRPS = -\sum_{i=1}^{n} \int \left(F(y| \hat{\theta}_i \left(\textbf{x}_i^*\right) -\textbf{I}\left(y \ge y^*_i\right)\right)^2 dy,\]
• \[MAPE= \texttt{med} \left(\left|100 \left(\frac{\hat{\mu}_i(\textbf{x}_i^*)-y^*}{y^*}\right) \right|_{i=1,\ldots.n}\right)\]

prediction measures table

models	LS	CRPS
mlinear	-6.2302	73.5738
madditive	-6.2288	73.8201
mfneural	-6.5126	79.9394
mregtree	-6.2930	78.6704
mcf	-6.2966	79.0644

Results would vary with different partitions of the data.

summary

• the GAIC is well established and tested (the df of freedom need to be known)

• the linear and additive model are good when there are not many explanatory variables (but somehow interactions have to be considered)

• more work has to be done to standardised all ML techniques so their partitioning of data are comparable to the conventional additive models

end

back to the index

The Books