Why GAMLSS?
Introduction
DAY 1
Morning
why GAMLSSAvailable softwarePractical 1
Afternoon
DistributionsContinuous distributionsPractical 2
DAY 2
Morning
Discrete DistributionsMixed distributionsPractical 3
Afternoon
Model FittingModel SelectionPractical 4
DAY 3
Morning
Centile estinationDiagnostics and ggplotsPractical 5
Afternoon
Model ComparisonModel InterpretationDiscussion
Why GAMLSS
Statistical modelling
Ditributional Regression
Statistical modelling
Statistical models
“all models are wrong but some are useful”.
– George Box
Models should be parsimonious
Models should be fit for purpose and able to answer the question at hand
Statistical models have a stochastic component
All models are based on assumptions.
Assumptions
Assumptions are made to simplify things
Explicit assumptions
Implicit assumptions
it is easier to check the explicit assumptions rather the implicit ones
Model circle
Regression
- \[ X \stackrel{\textit{M}(\theta)}{\longrightarrow} Y \]
- \(y\): targer, the y or the dependent variable
- \(X\): explanatory, features, x’s or independent variables or terms
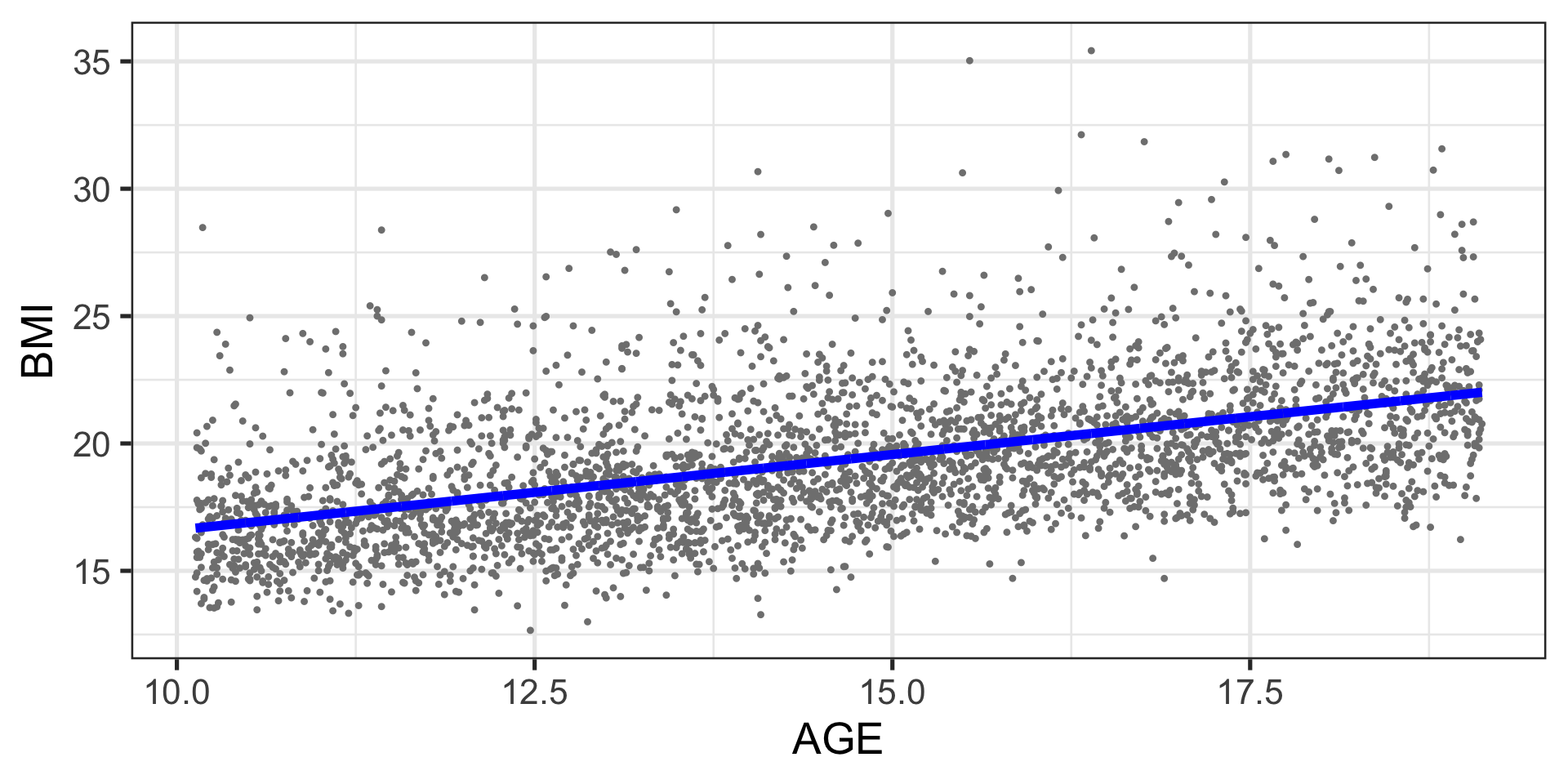
Linear Model
- standard way
\[ \begin{equation} y_i= b_0 + b_1 x_{1i} + b_2 x_{2i}, \ldots, b_p x_{pi}+ \epsilon_i \end{equation} \qquad(1)\]
Linear Model
- different way
\[ \begin{split} y_i & \stackrel{\small{ind}}{\sim } & {N}(\mu_i, \sigma) \nonumber \\ \mu_i &=& b_0 + b_1 x_{1i} + b_2 x_{2i}, \ldots, b_p x_{pi} \end{split} \qquad(2)\]
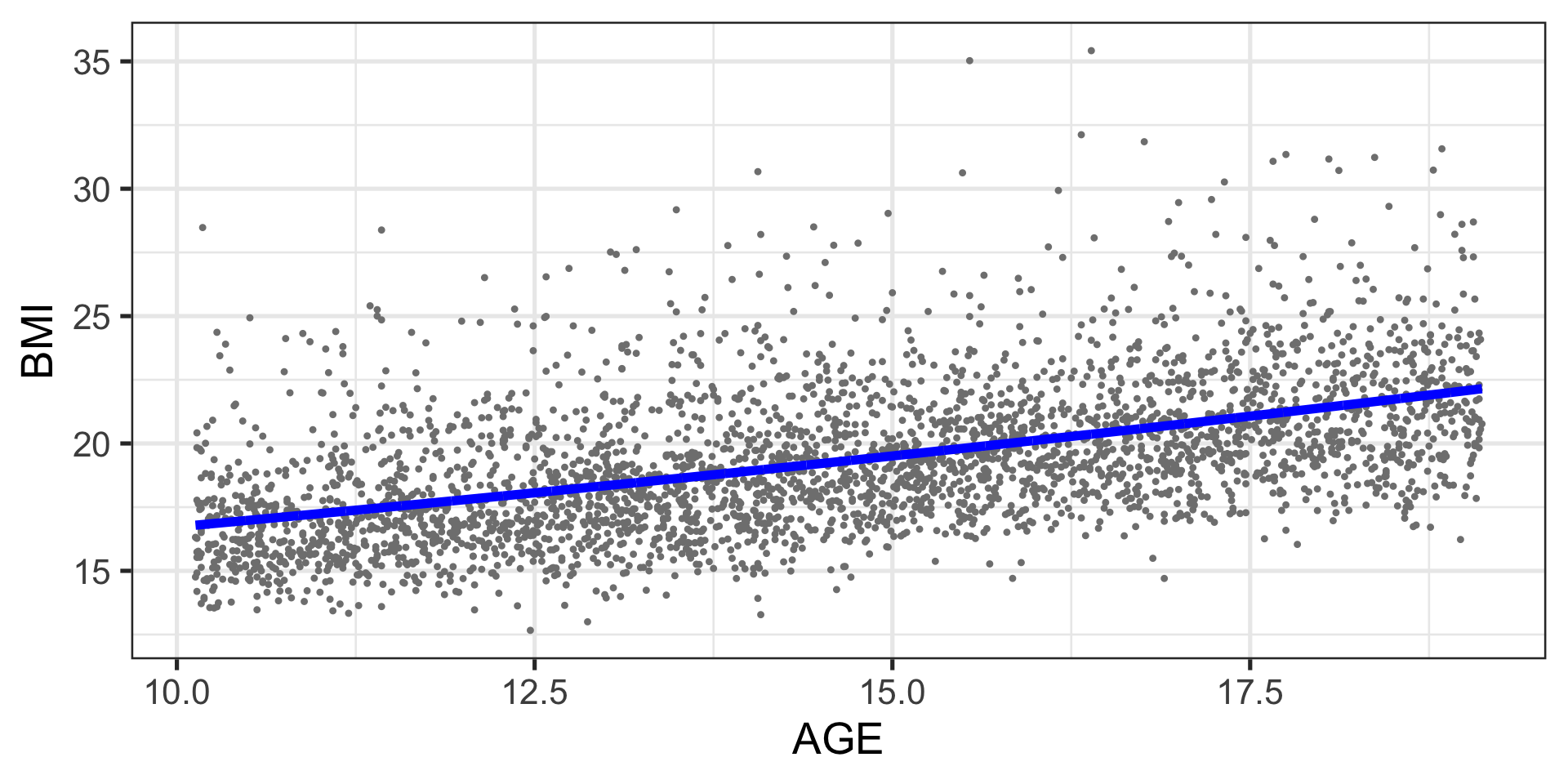
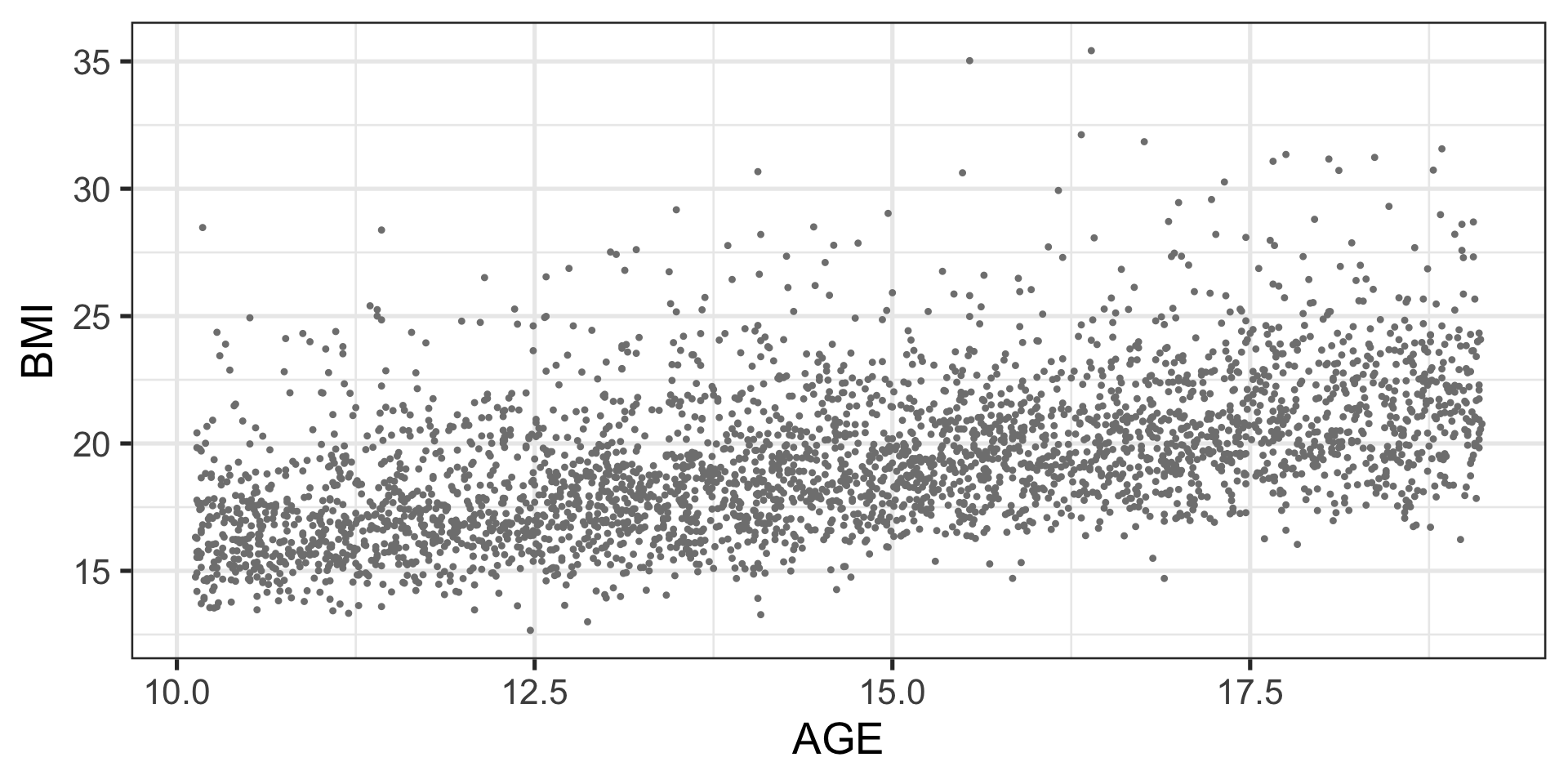
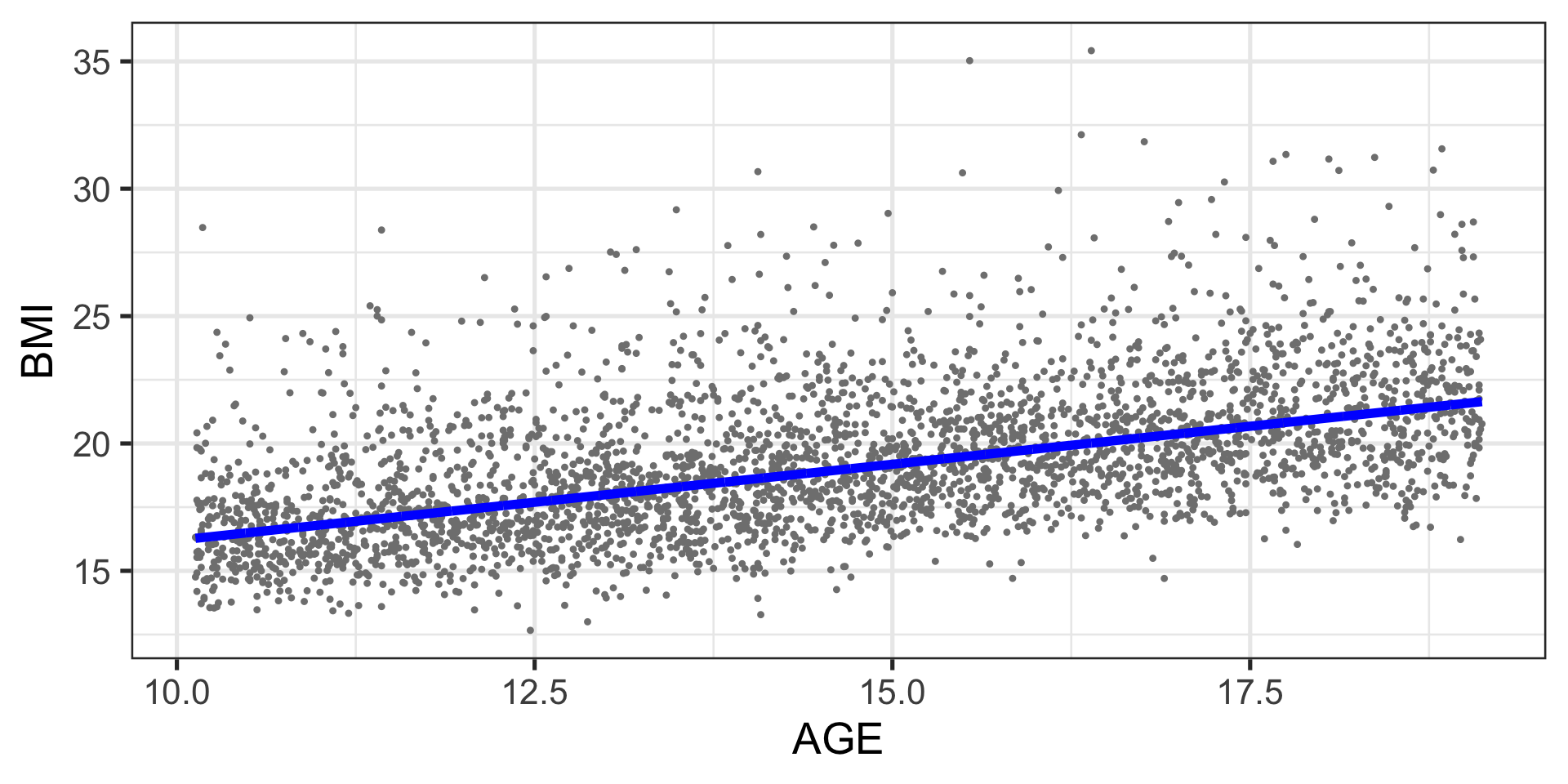
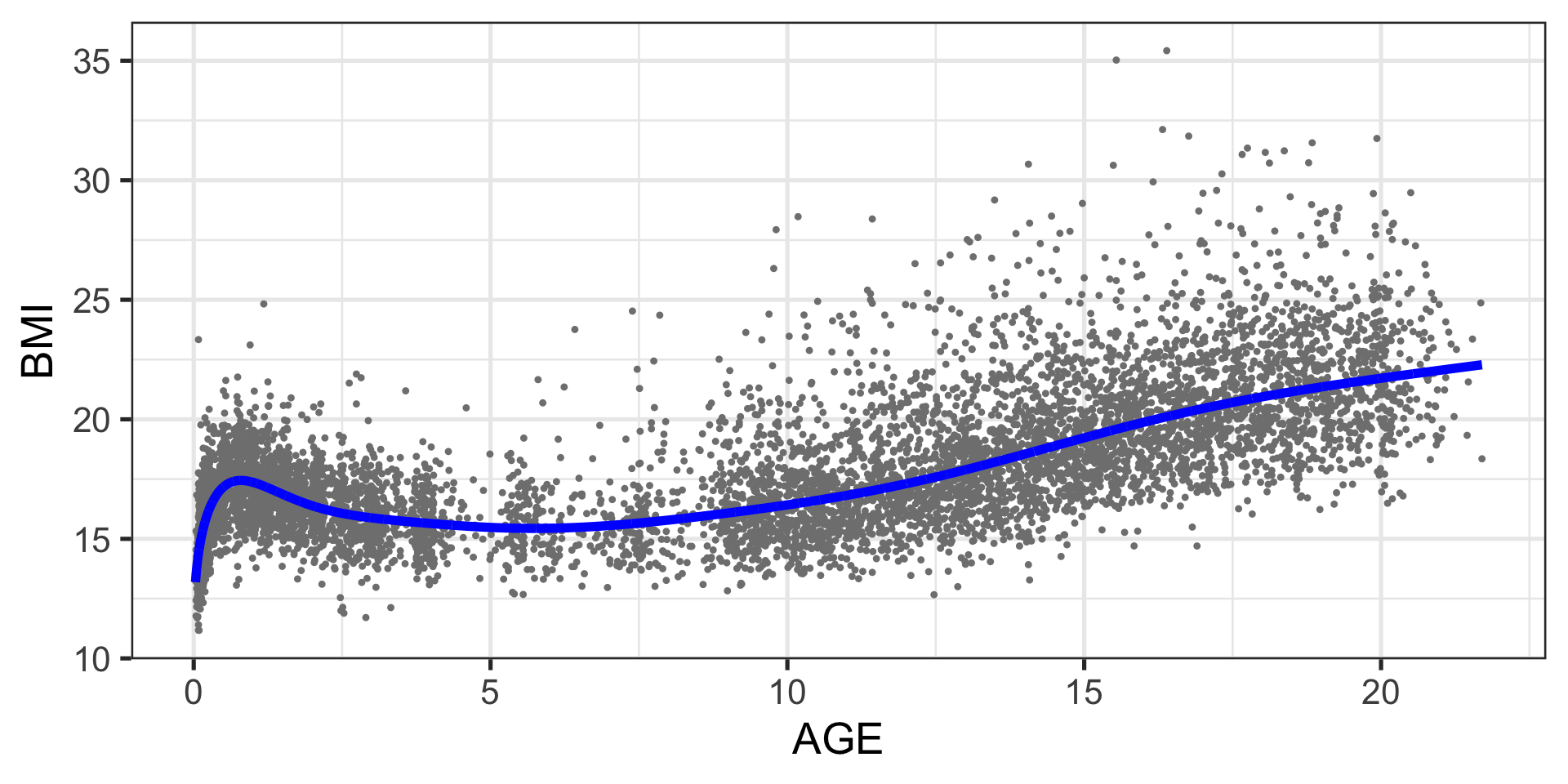
Example: BMI data
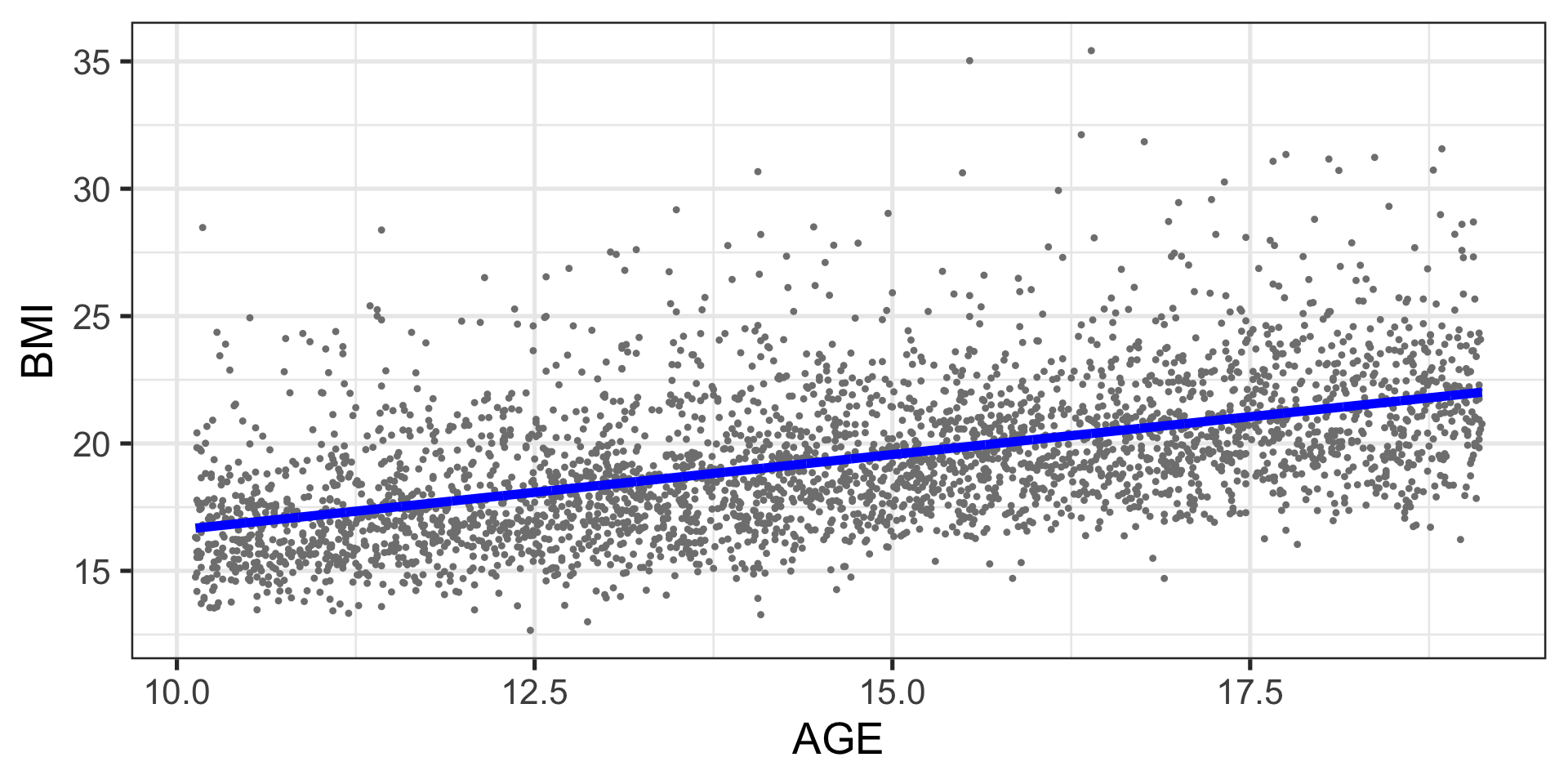
Example: BMI fitted model
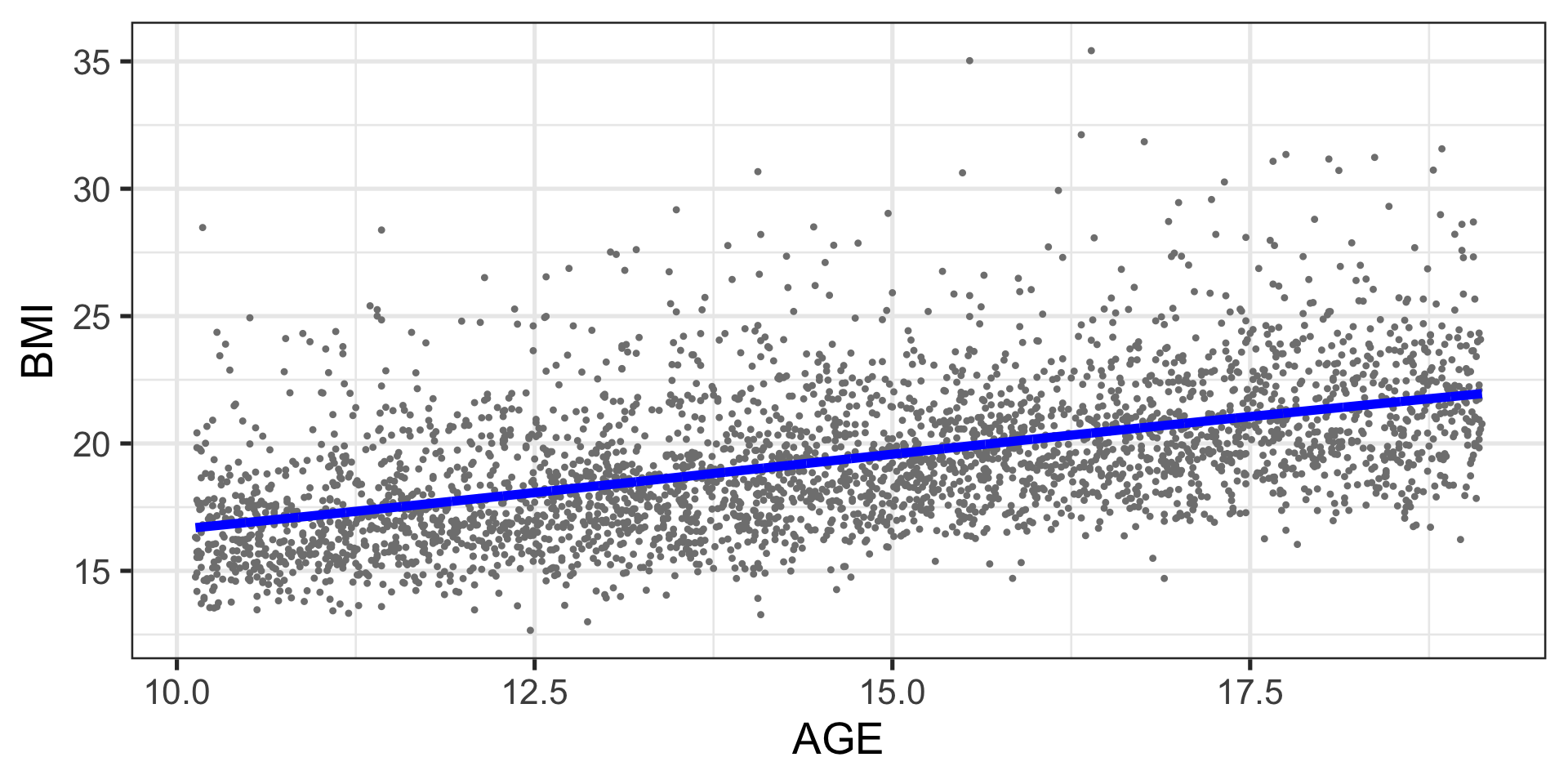
Additive Models
\[ \begin{split} y_i & \stackrel{\small{ind}}{\sim } & {N}(\mu_i, \sigma) \nonumber \\ \mu_i &=& b_0 + s_1(x_{1i}) + s_2(x_{2i}), \ldots, s_p(x_{pi}) \end{split} \qquad(3)\]
Example: additive fitted model
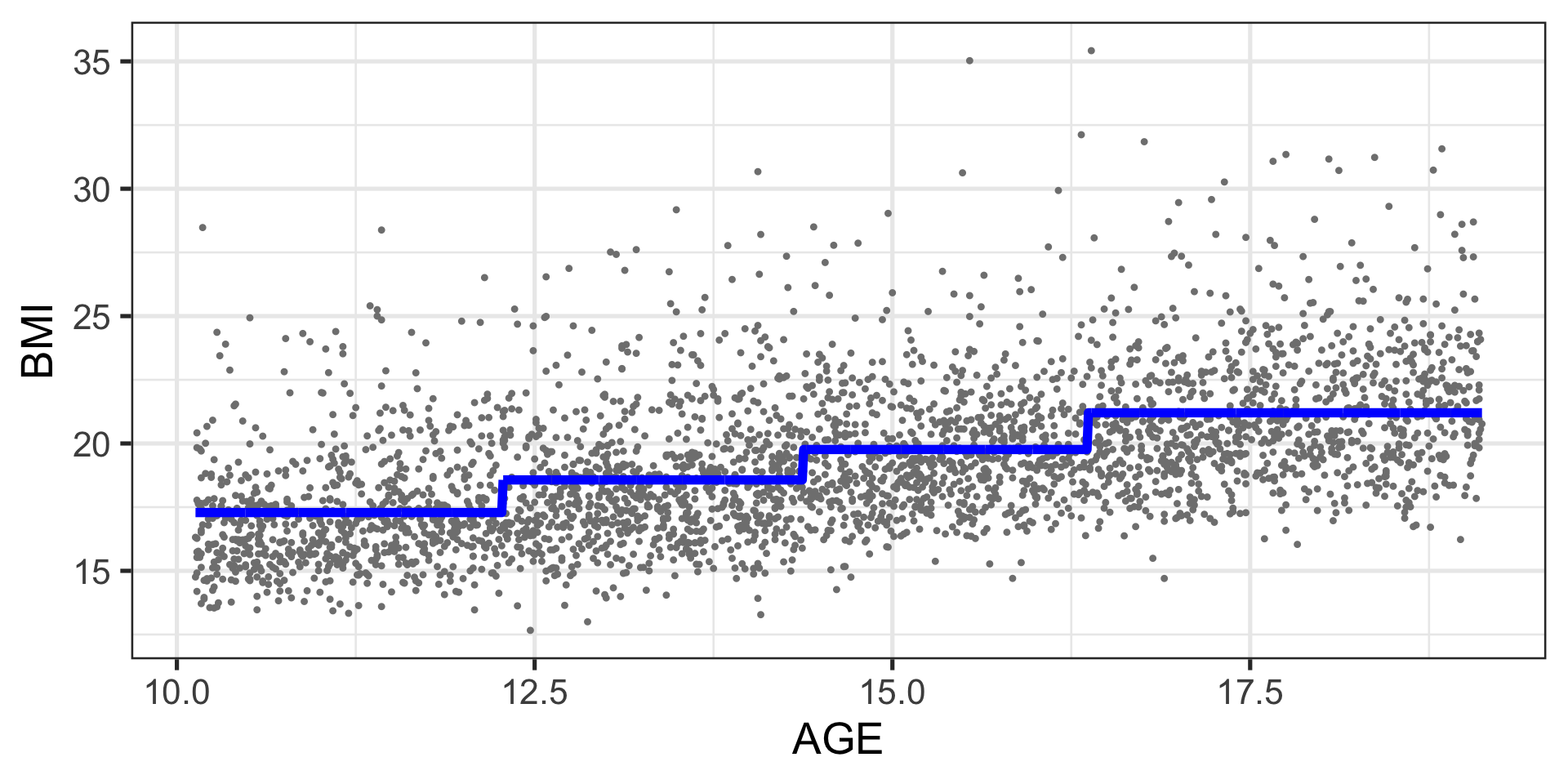
Machine Learning Models
\[\begin{split} y_i & \stackrel{\small{ind}}{\sim }& {N}(\mu_i, \sigma) \nonumber \\ \mu_i &=& ML(x_{1i},x_{2i}, \ldots, x_{pi}) \end{split} \qquad(4)\]
Example: neural networks
Example: regression tree
Generalised Linear Models
\[\begin{split} y_i & \stackrel{\small{ind}}{\sim }& {E}(\mu_i, \phi) \nonumber \\ g(\mu_i) &=& b_0 + b_1 x_{1i} + b_2 x_{2i}, \ldots, b_p x_{pi} \end{split} \qquad(5)\]
\({E}(\mu_i, \phi)\) :
Exponentialfamily\(g(\mu_i)\) : the
linkfunction
Example: GLM
Example: diagnostics 1
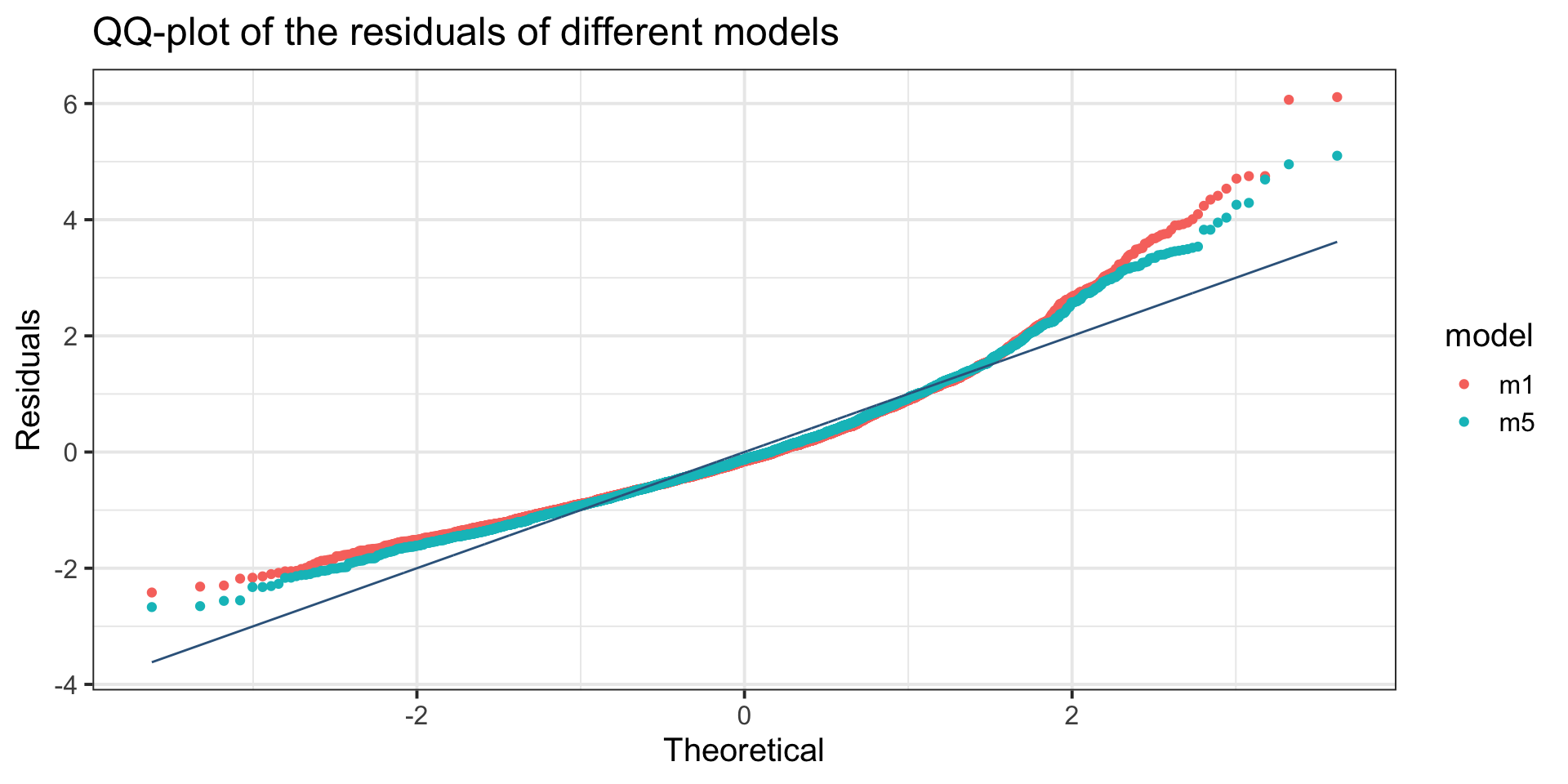
Example: diagnostics 2
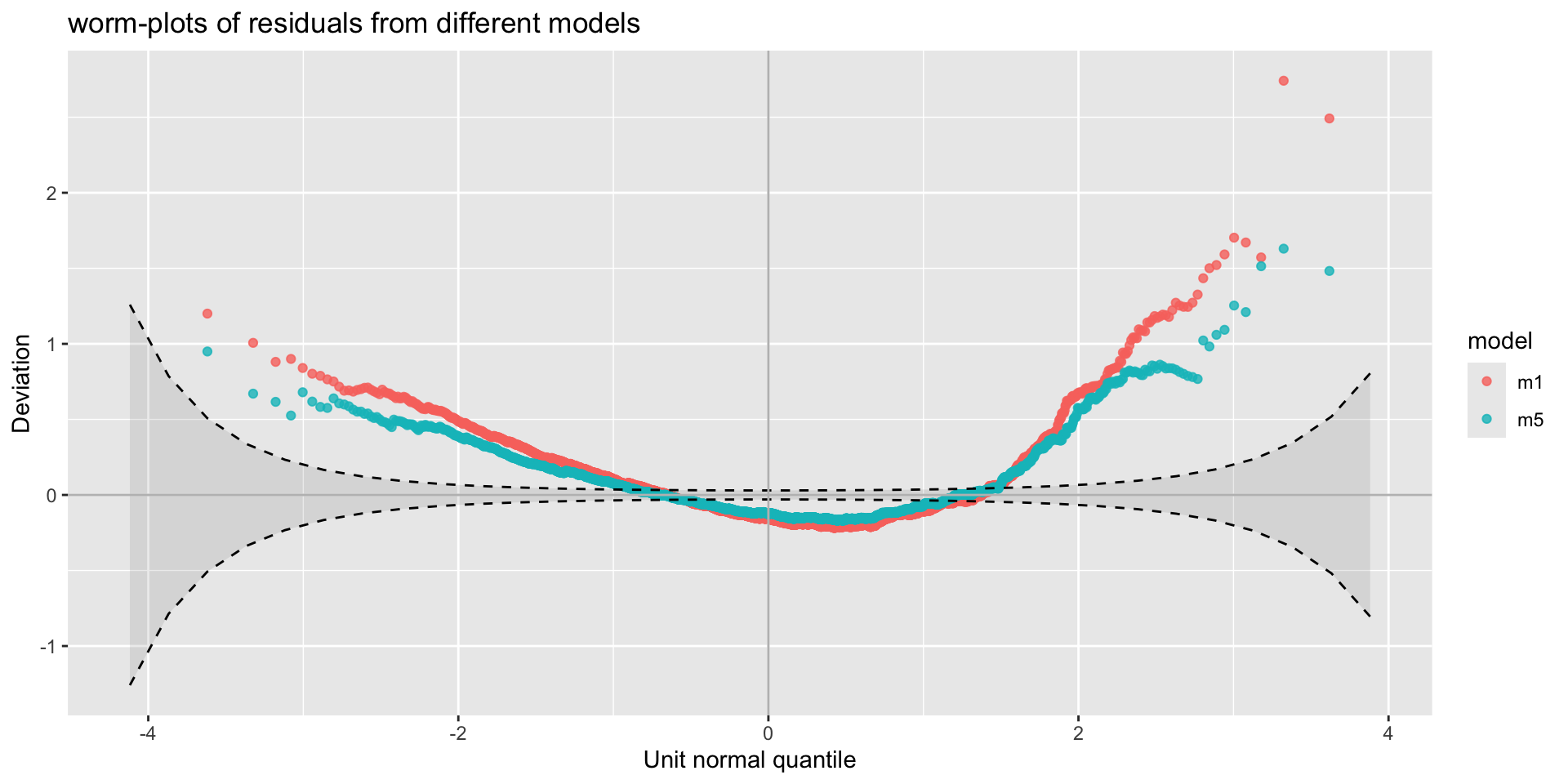
Example: diagnostics 3
Example: conclusion
the
meanof the response is fitted fine with the linear model but the distribution is notthe distribution (implicit
Normal) is not-adequateeven the explicit
Gammadistribution of the GLM is not-adequatetherefore if we are interested on a statistic different from the
meanwe need something extra.
Distributional regression
Distributional regression
\[ X \stackrel{\textit{M}(\boldsymbol{\theta})}{\longrightarrow} D\left(Y|\boldsymbol{\theta}(\textbf{X})\right) \]
All parameters \(\boldsymbol{\theta}\) could functions of the explanatory variables \(\boldsymbol{\theta}(\textbf{X})\).
\(D\left(Y|\boldsymbol{\theta}(\textbf{X})\right)\) can be any \(k\) parameter distribution
Generalised Additive models for Location Scale and Shape
\[\begin{split} y_i & \stackrel{\small{ind}}{\sim }& {D}( \theta_{1i}, \ldots, \theta_{ki}) \nonumber \\ g(\theta_{1i}) &=& b_{10} + s_1({x}_{1i}) + \ldots, s_p({x}_{pi}) \nonumber\\ \ldots &=& \ldots \nonumber\\ g({\theta}_{ki}) &=& b_0 + s_1({x}_{1i}) + \ldots, s_p({x}_{pi}) \end{split} \qquad(6)\]
GAMLSS + ML
\[\begin{split} y_i & \stackrel{\small{ind}}{\sim }& {D}( \theta_{1i}, \ldots, \theta_{ki}) \nonumber \\ g({\theta}_{1i}) &=& {ML}_1({x}_{1i},{x}_{2i}, \ldots, {x}_{pi}) \nonumber \\ \ldots &=& \ldots \nonumber\\ g({\theta}_{ki}) &=& {ML}_1({x}_{1i},{x}_{2i}, \ldots, {x}_{pi}) \end{split} \qquad(7)\]
Example: GAMLSS
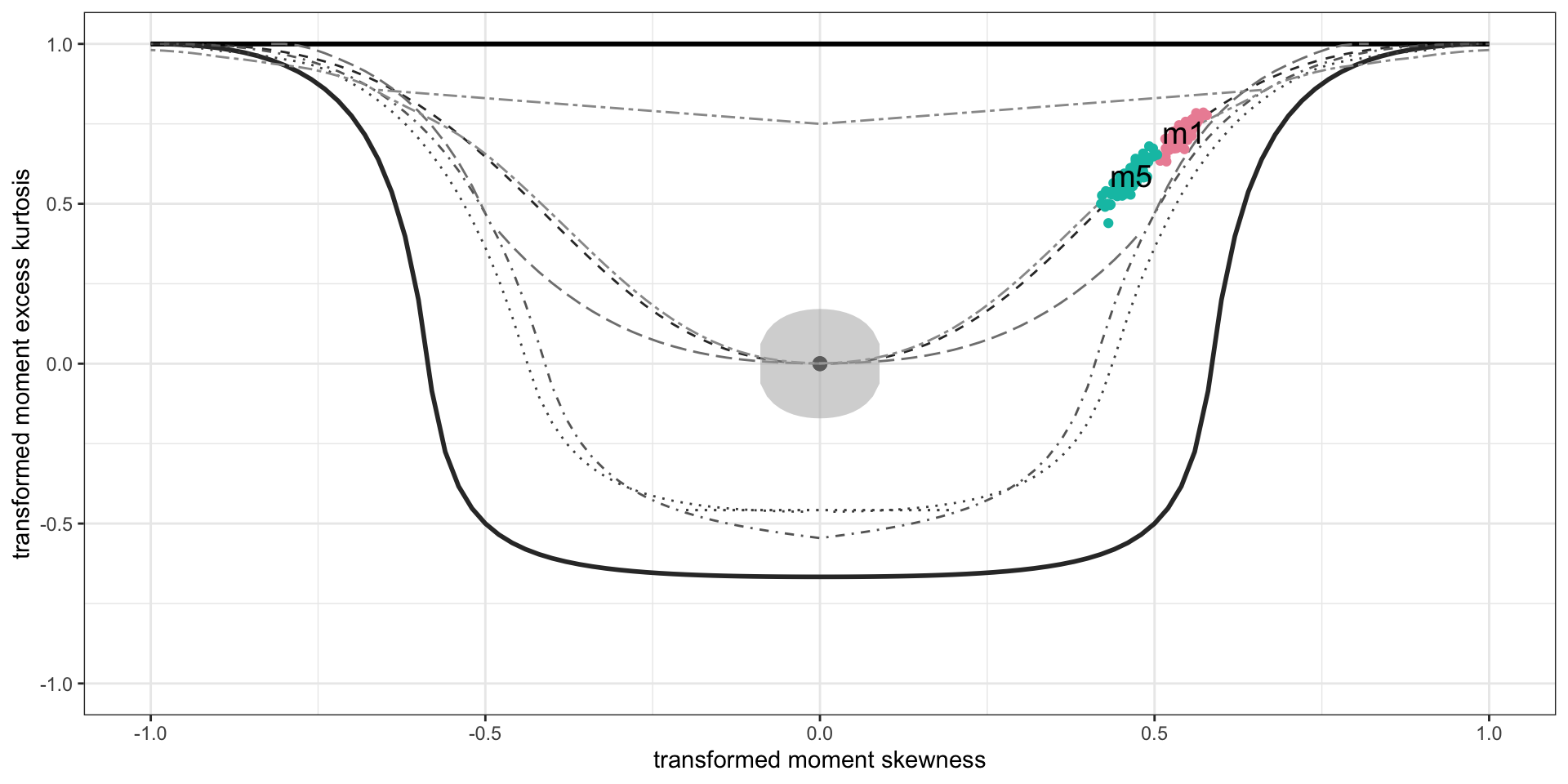
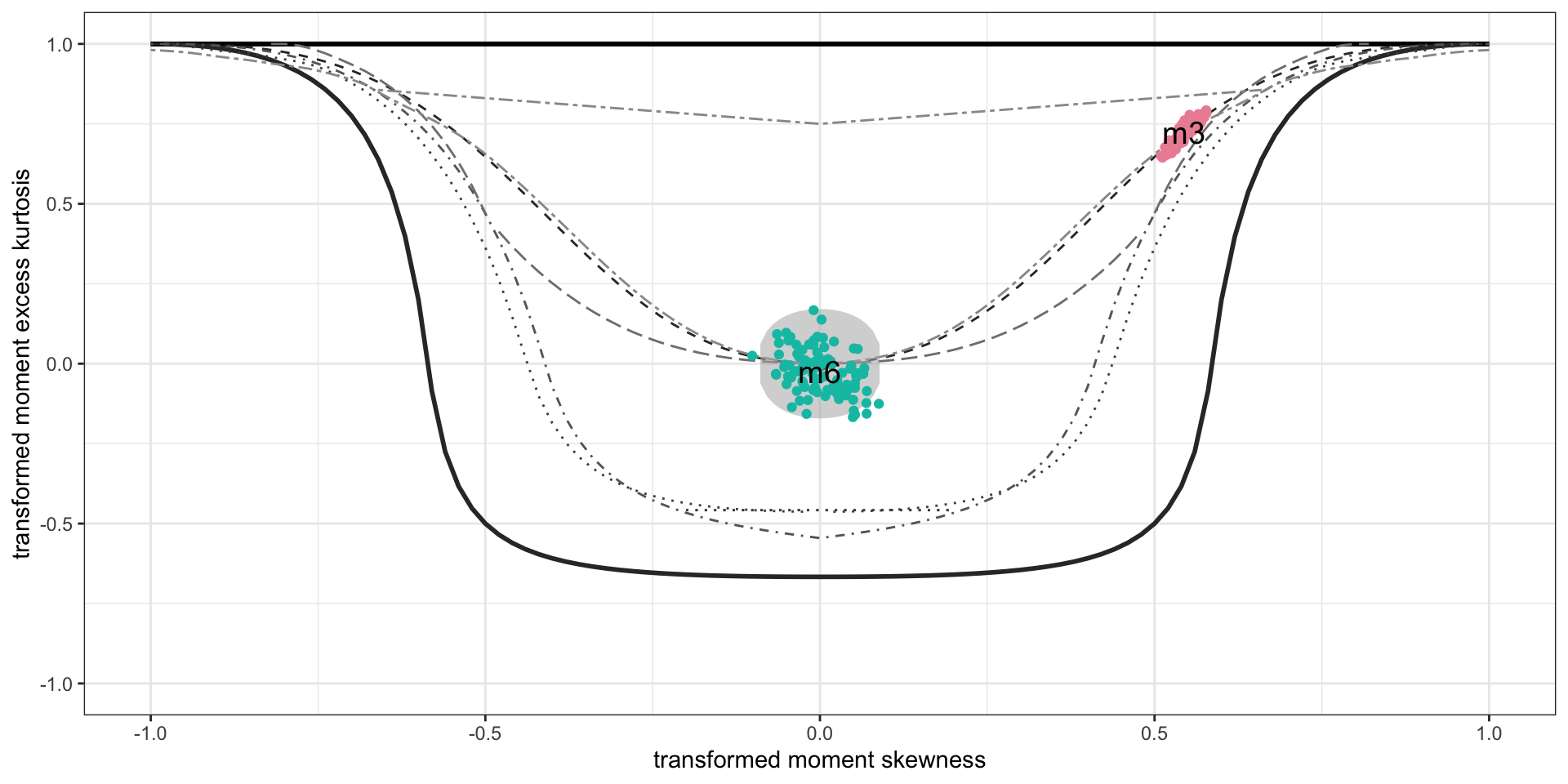
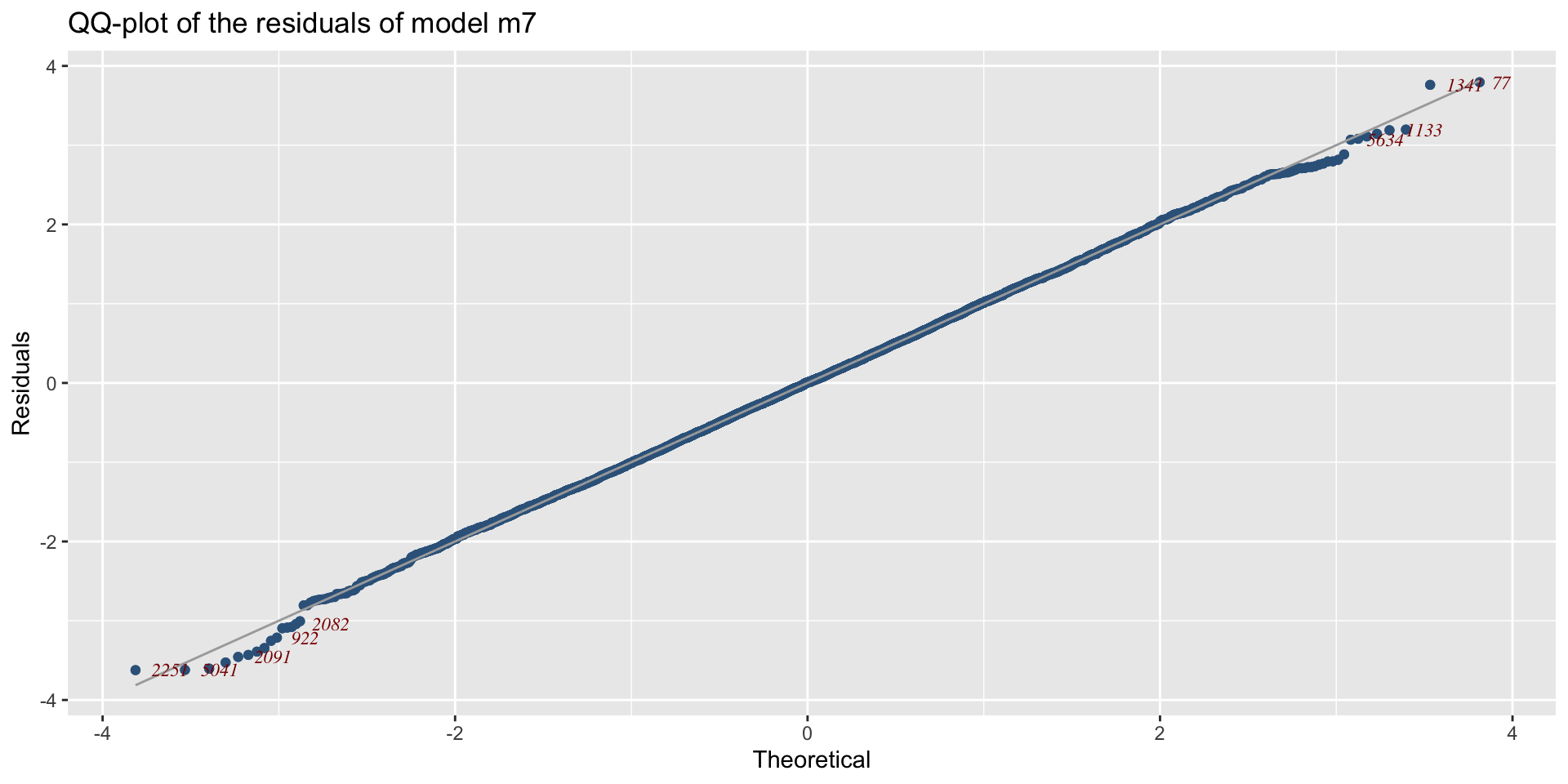
Example: diagnostics
Example: diagnostics 2
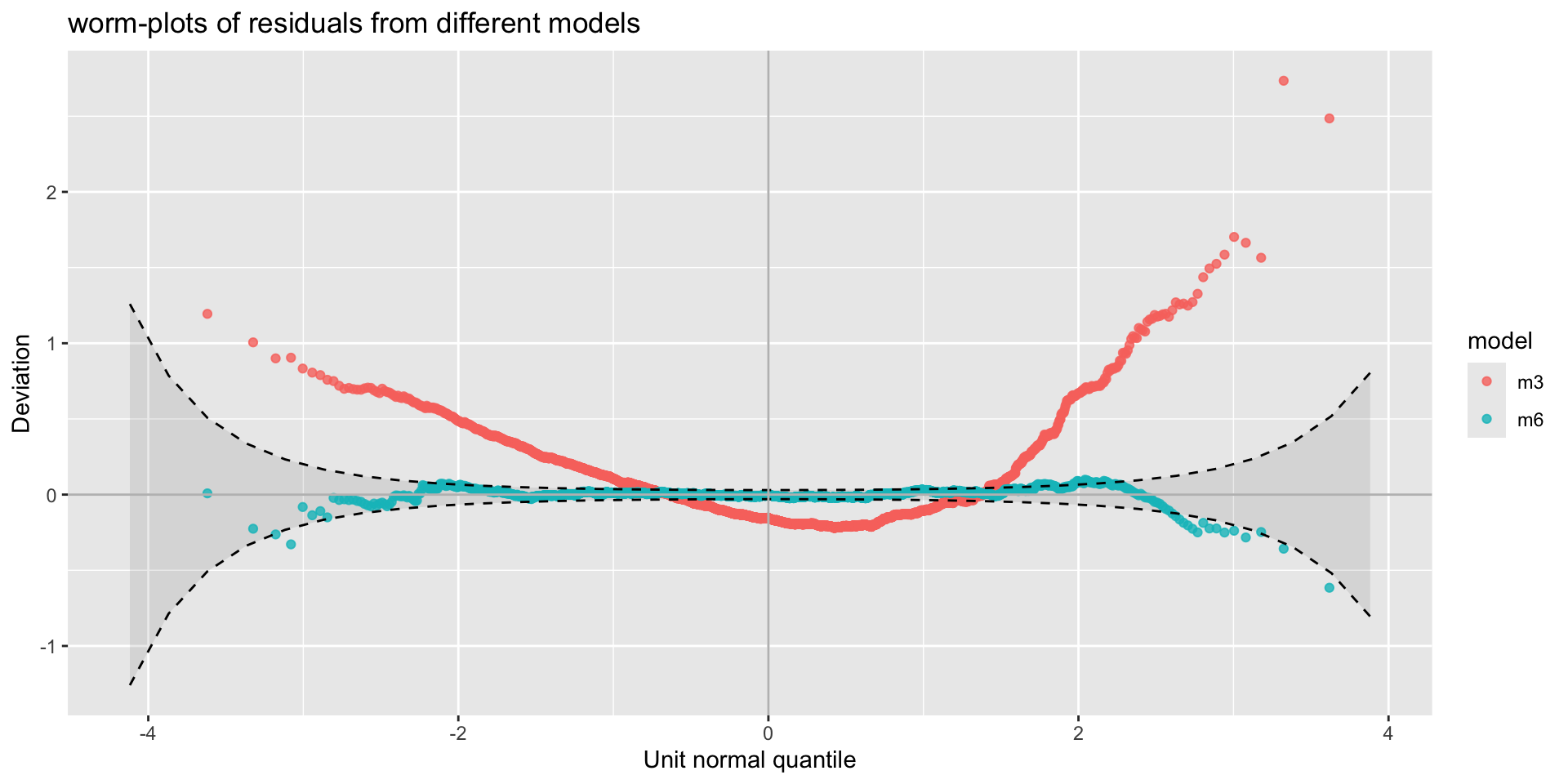
Example: diagnostics 3
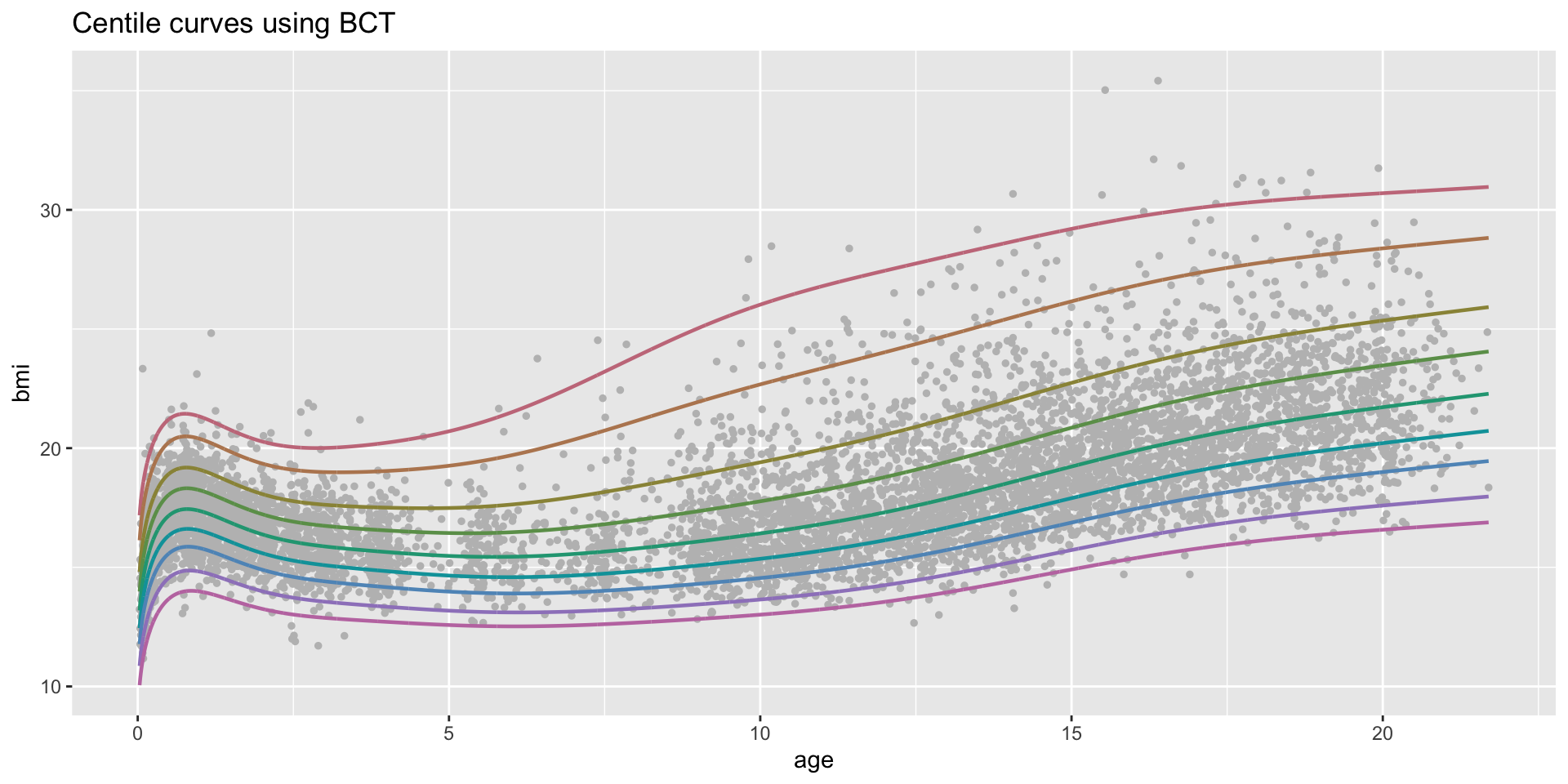
Fitted Centiles
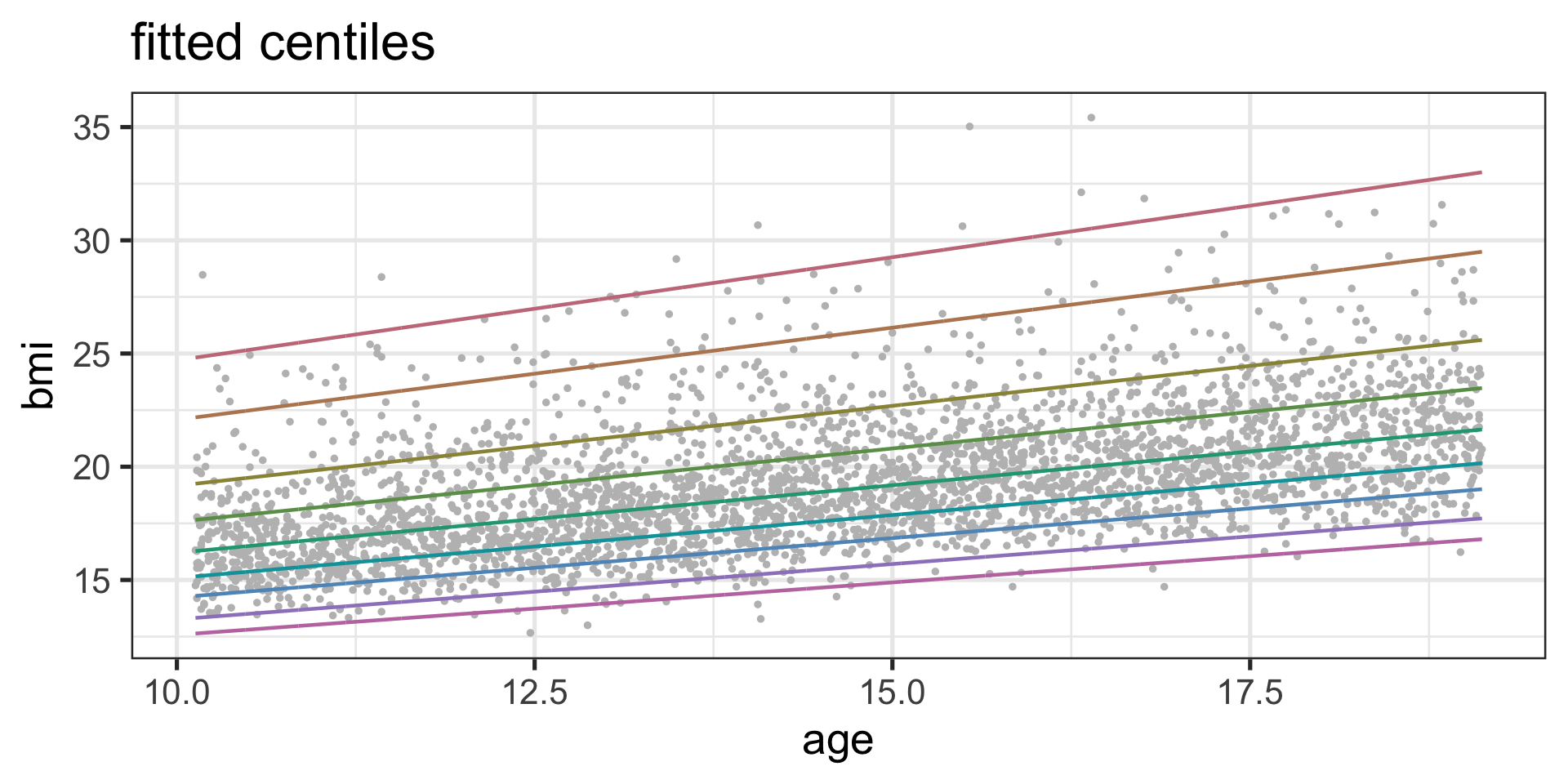
Figure 1: Centile-plot of the fitted m6 model
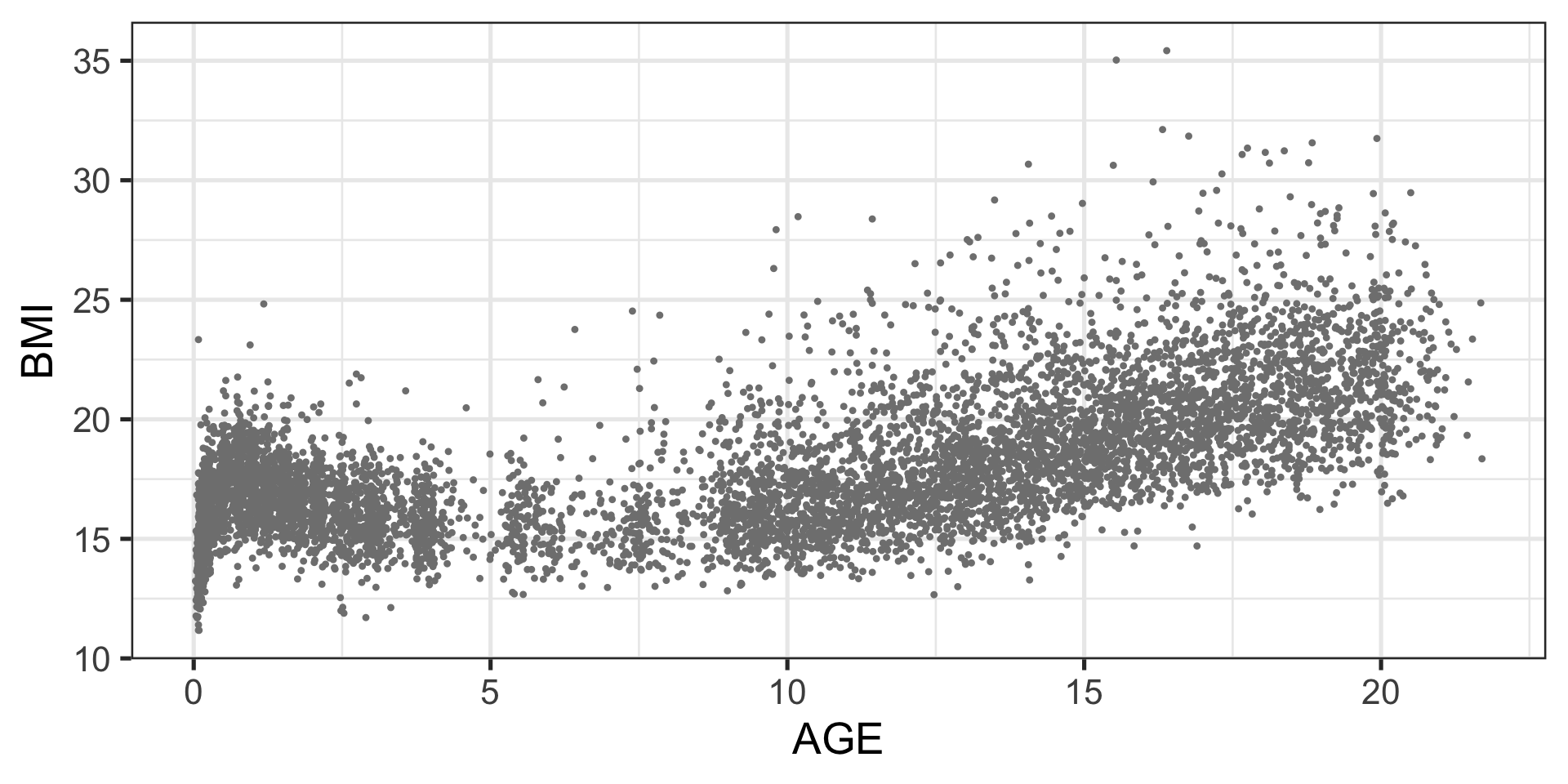
The true BMI data
The fitted model
The fitted centiles
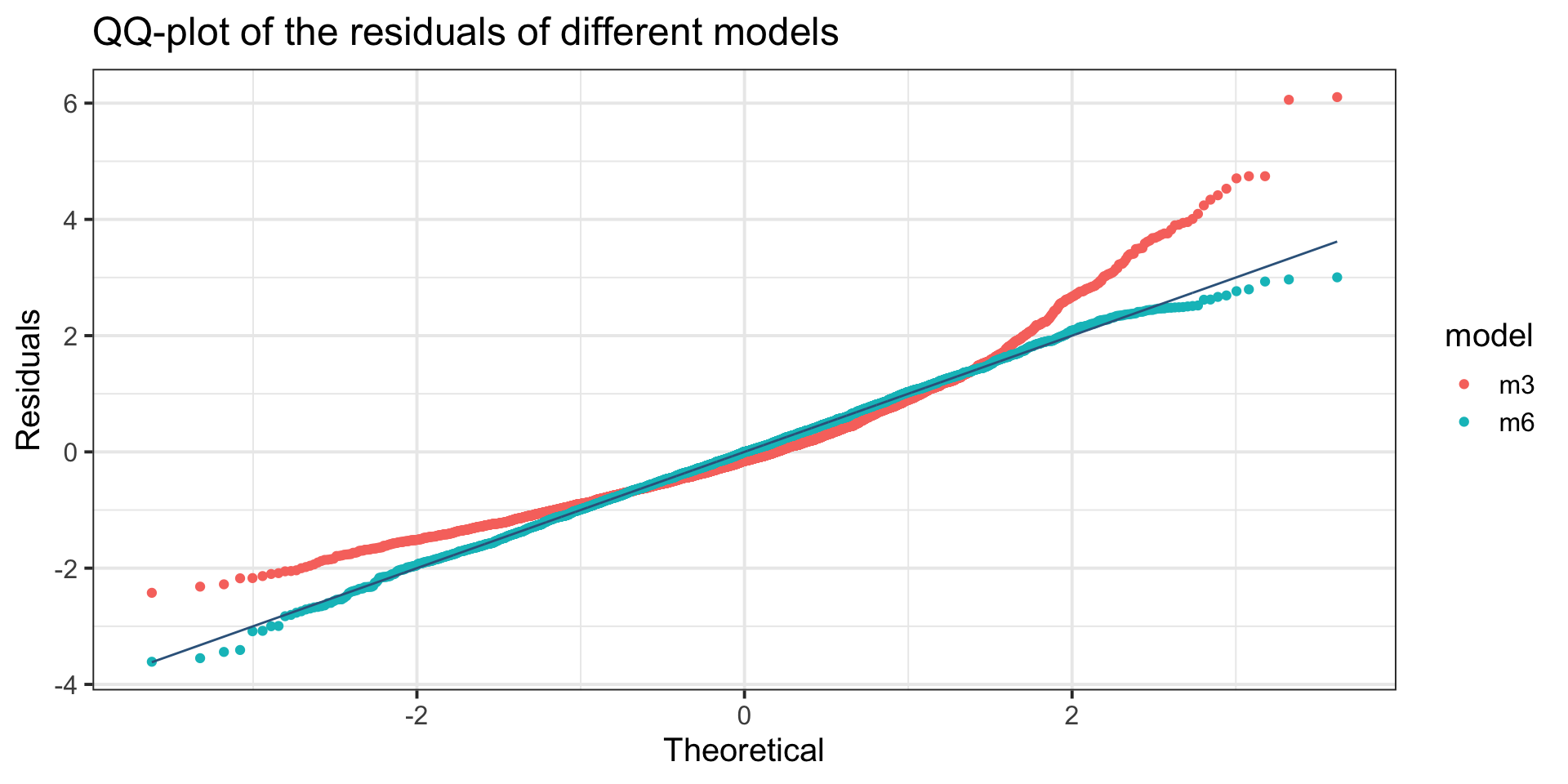
Diagnostics 1
Diagnostics 2
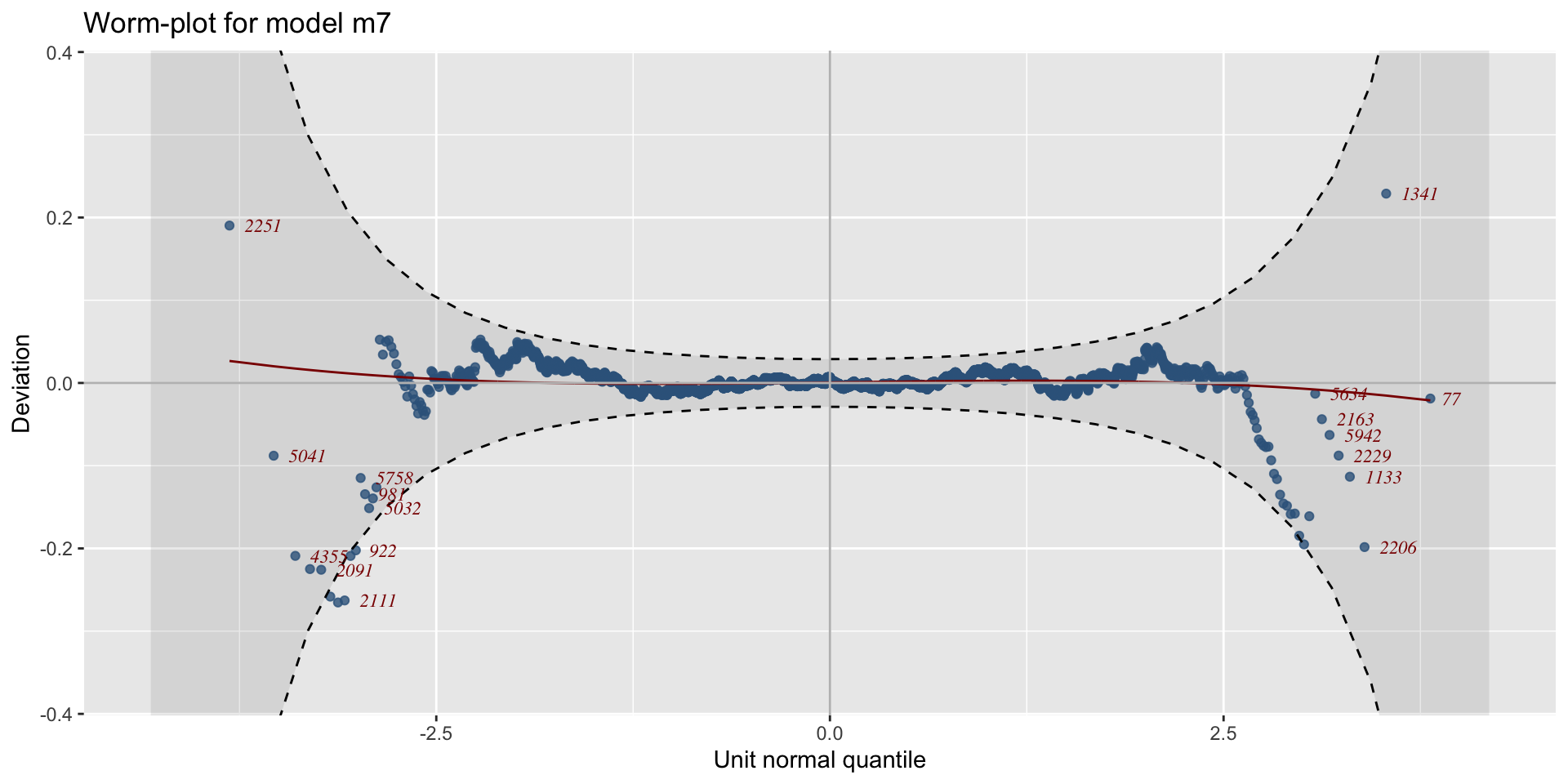
Diagnostics 3
Summary
Distributional assumptions often needed for the response to be fitted properly
In the BMI example above we needed to model all the parameters of the distribution as function of the explanatory variable
age.Those parameters were the
locationparameter \(\mu\), thescaleparameter, \(\sigma\), theskewnessparameter, \(\nu\), and thekurtoticparameter \(\tau\)Machine Learning methods are useful (especially for modelling interactions between variables) but they are not suitable if the interest do non lie in the mean.
end


 The Books
The Books

www.gamlss.com