A log family of distributions from SST has been generated
and saved under the names:
dlogSST plogSST qlogSST rlogSST logSST A zero adjusted logSST distribution has been generated
and saved under the names:
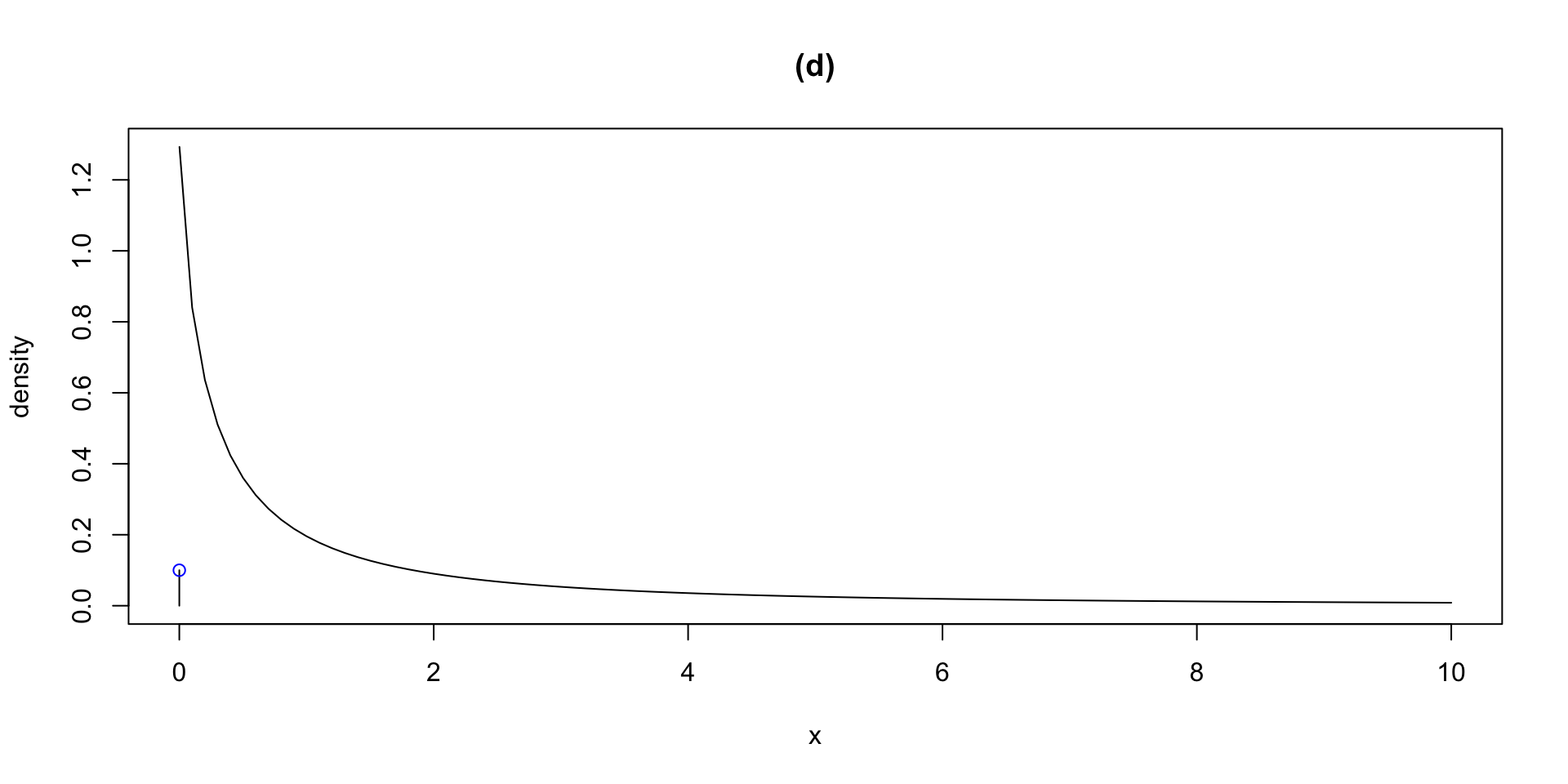
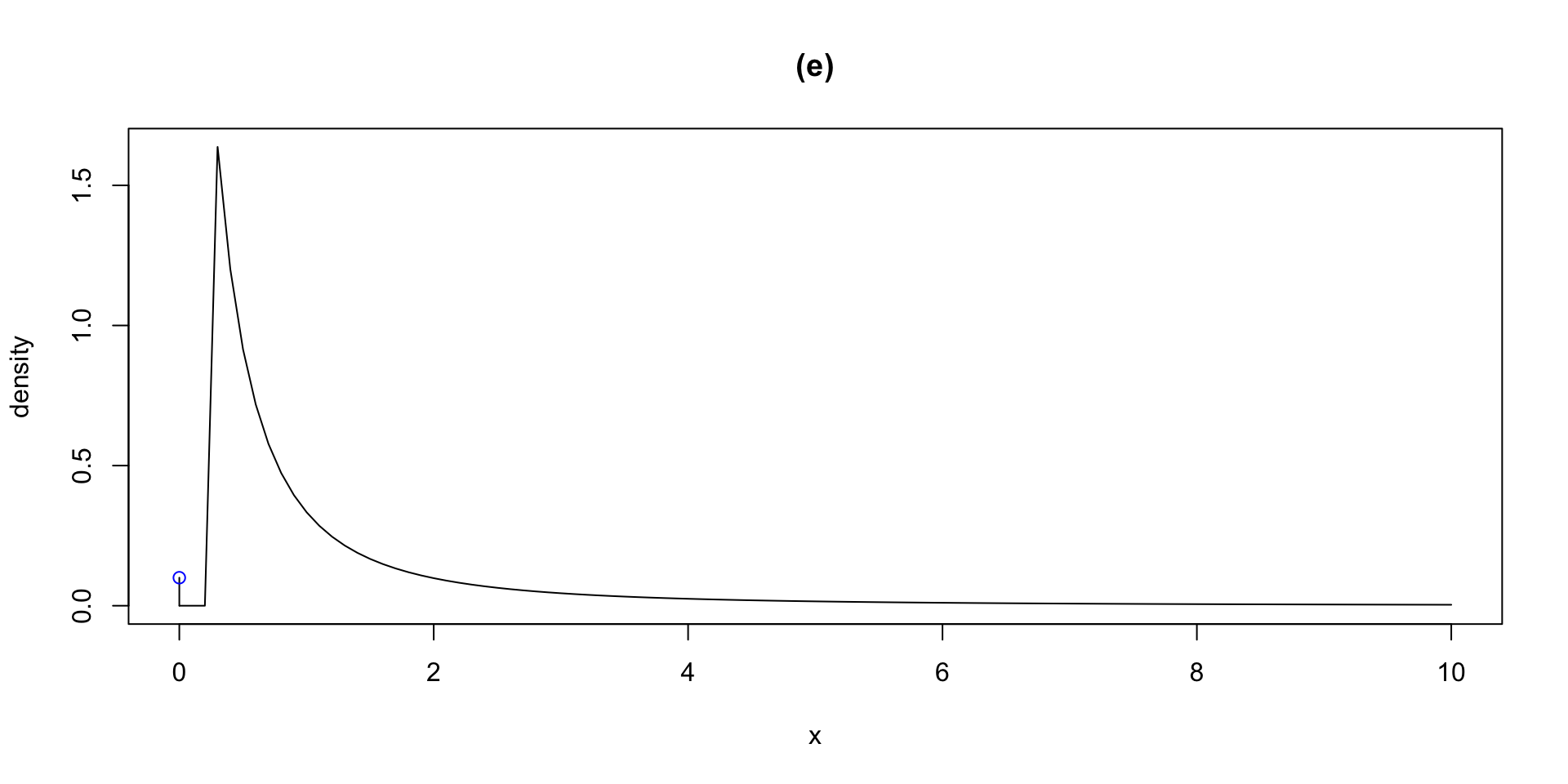
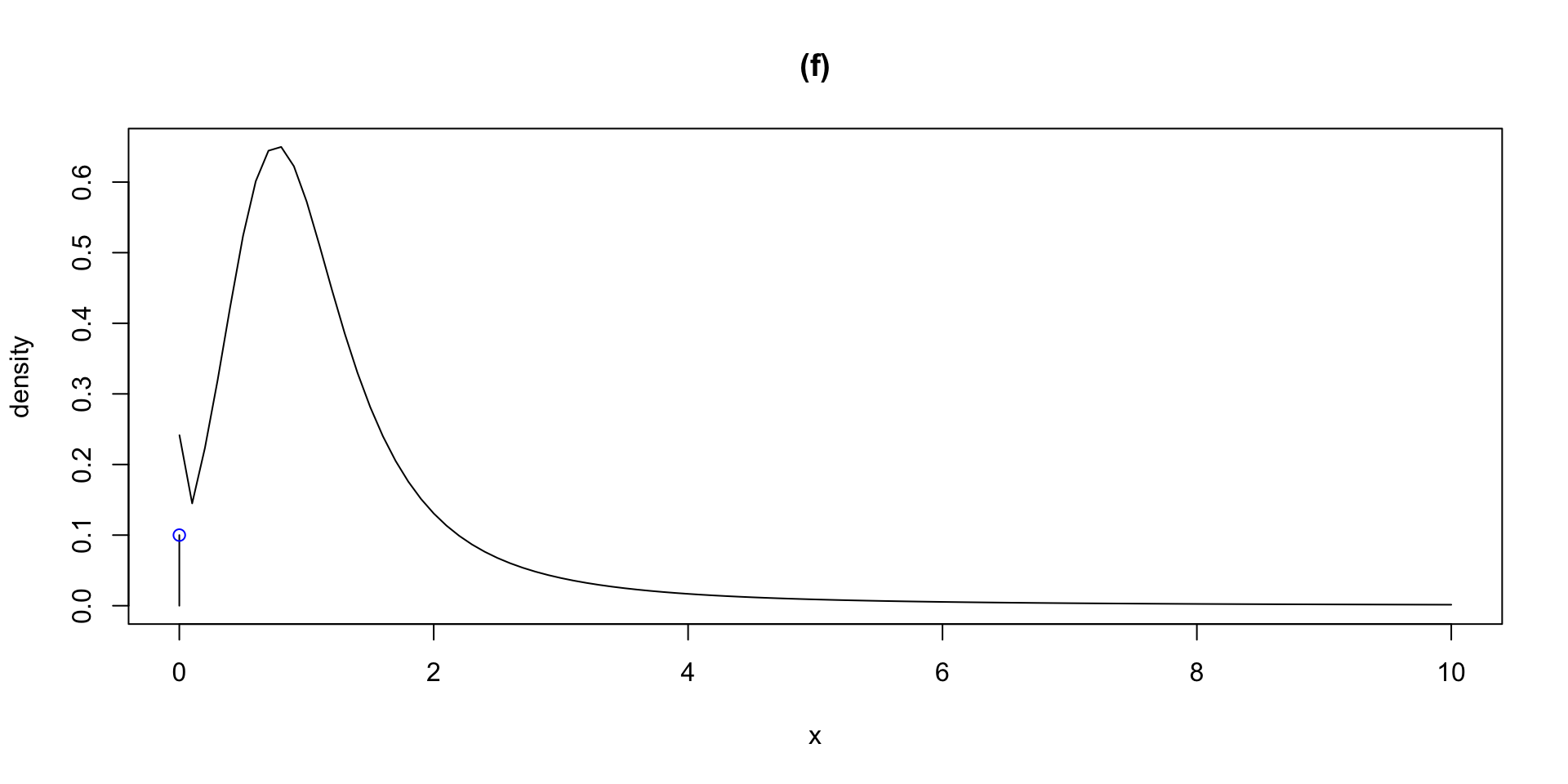
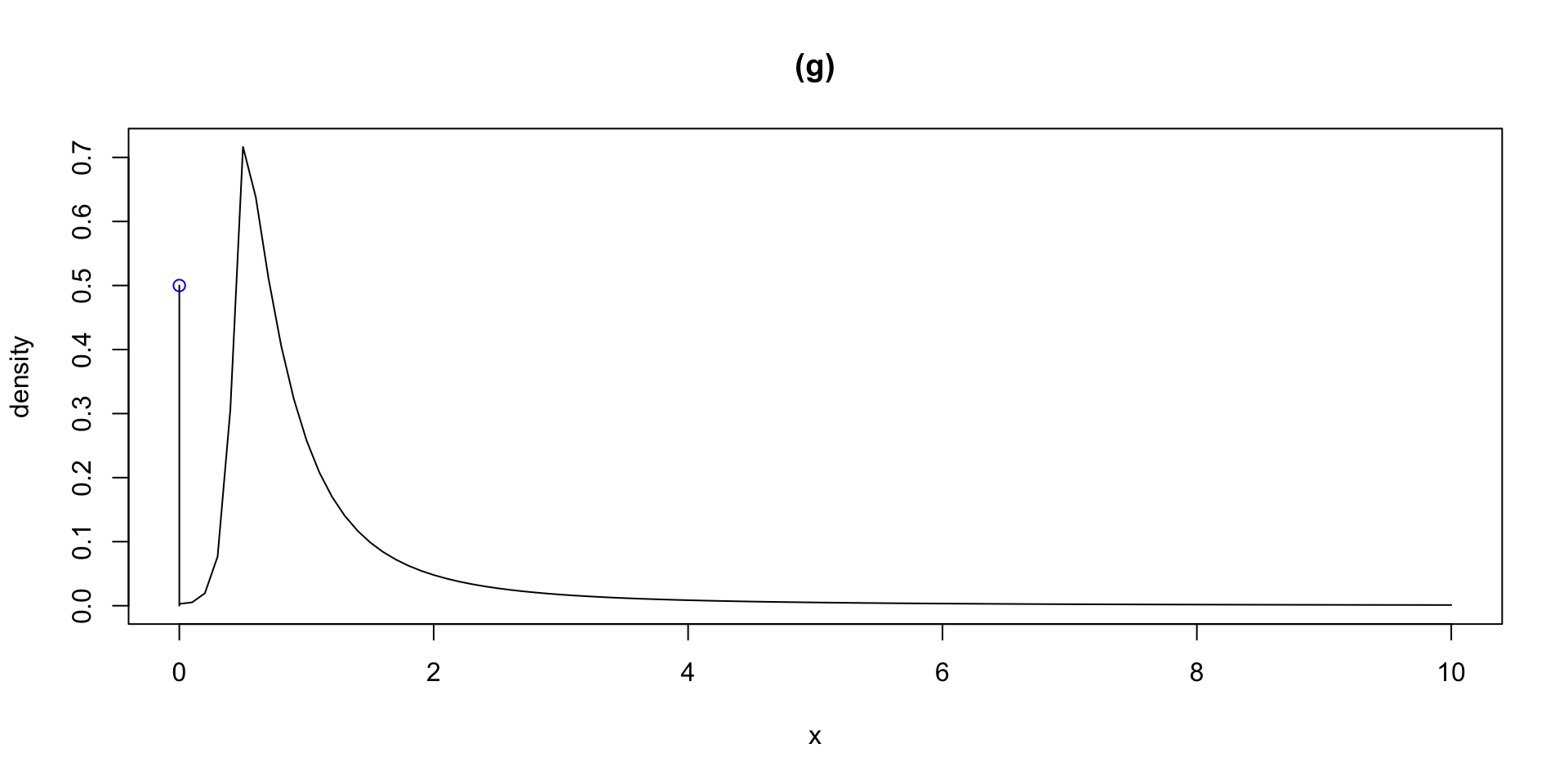
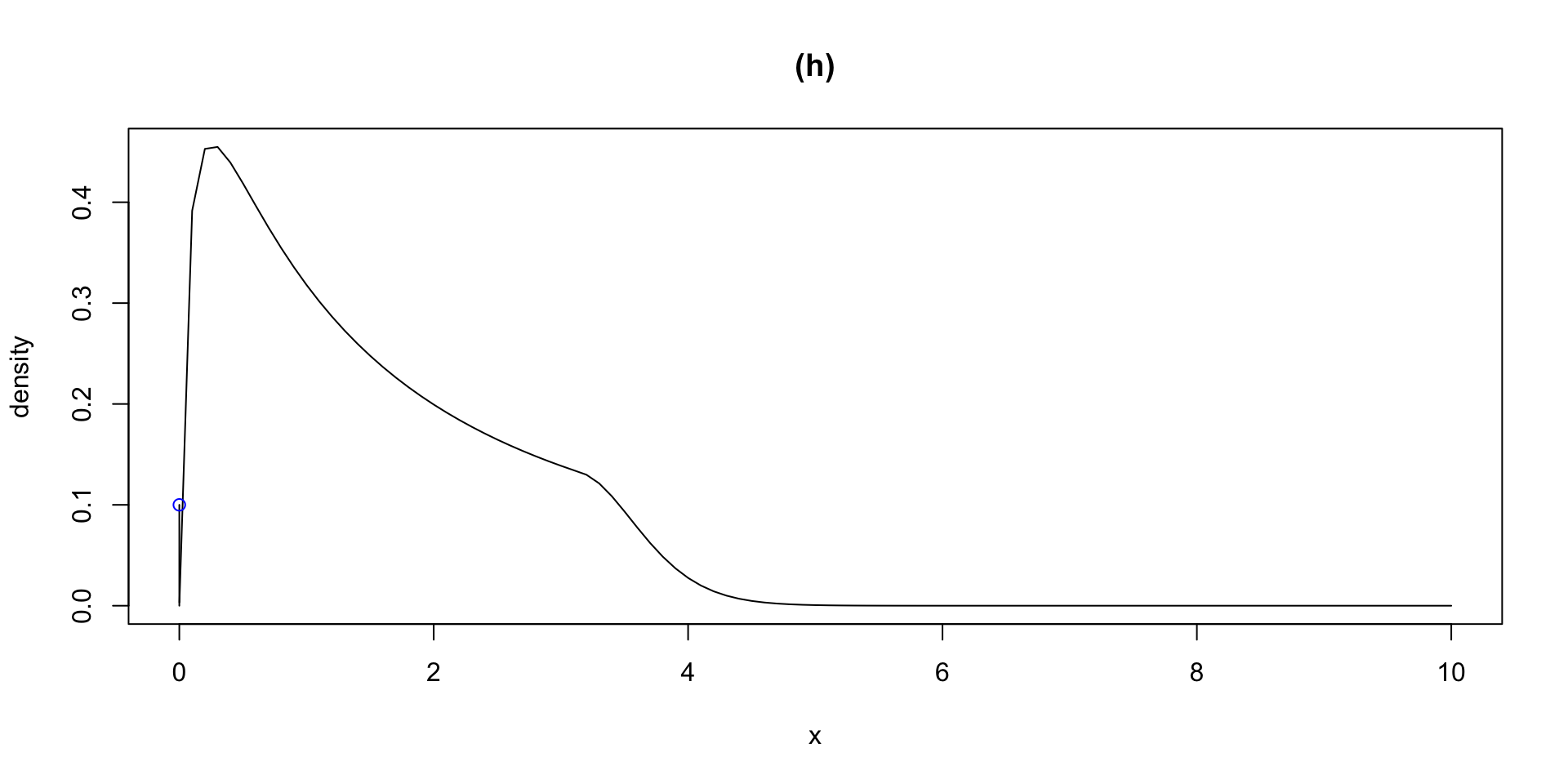
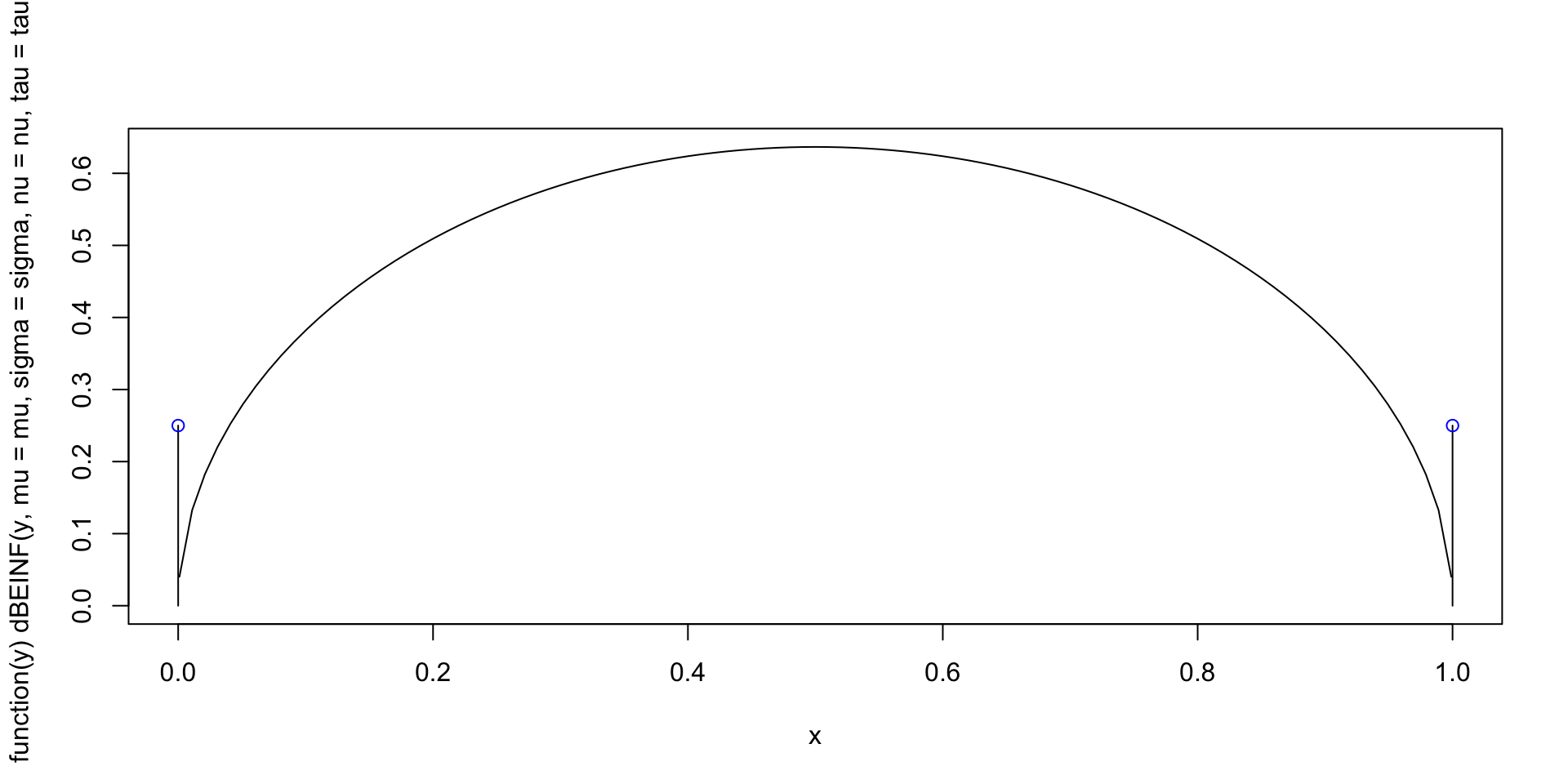
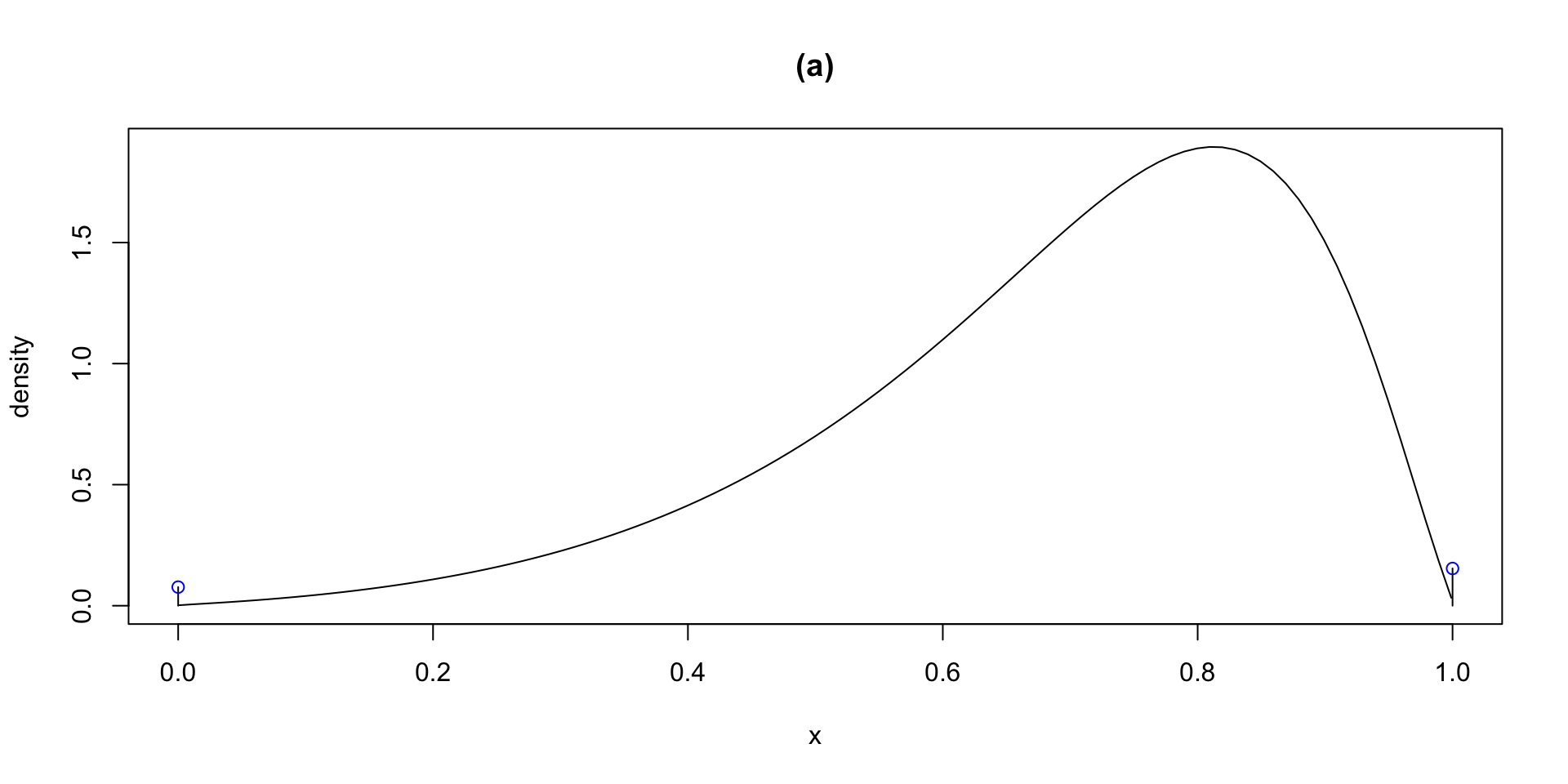
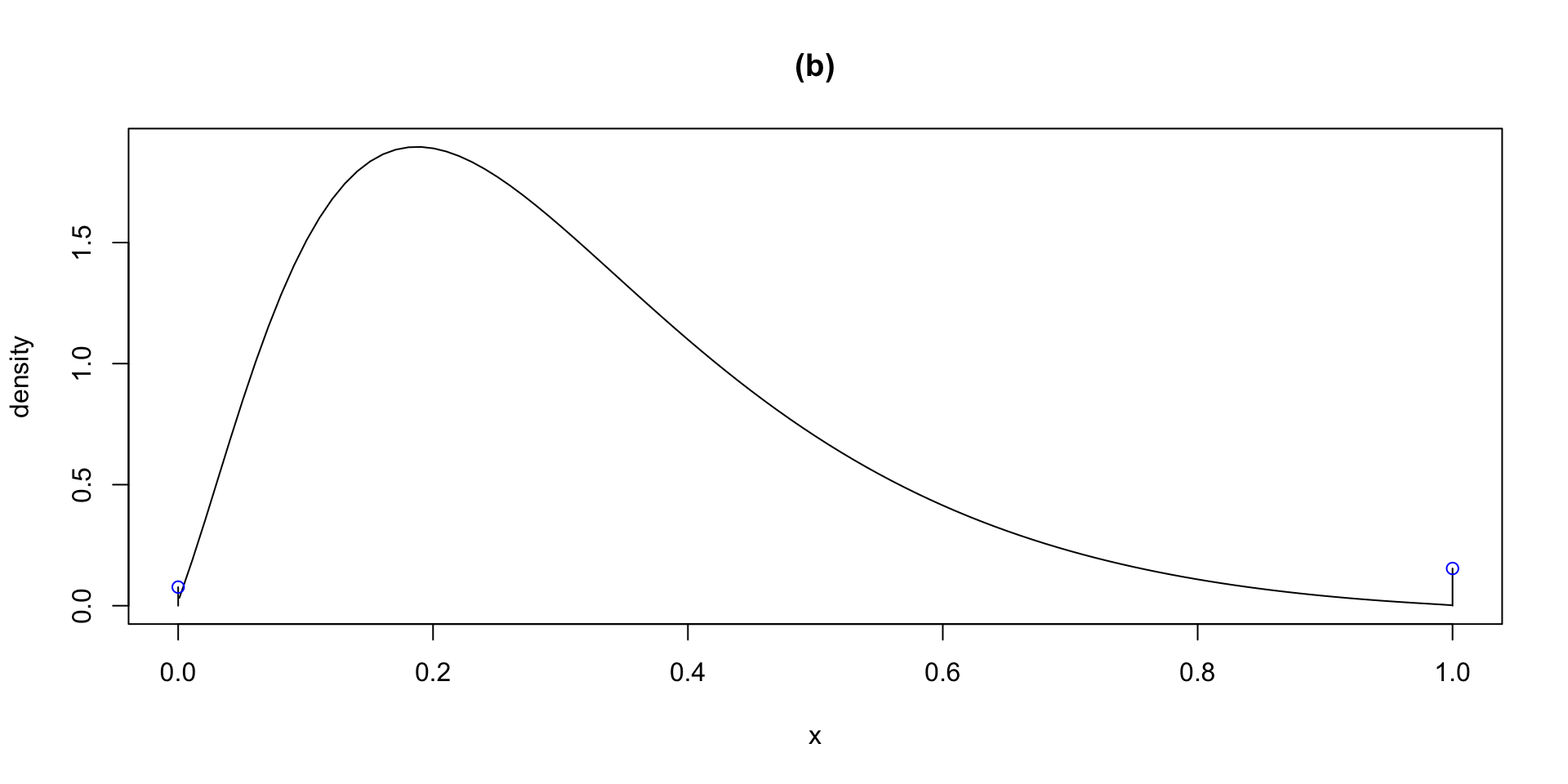
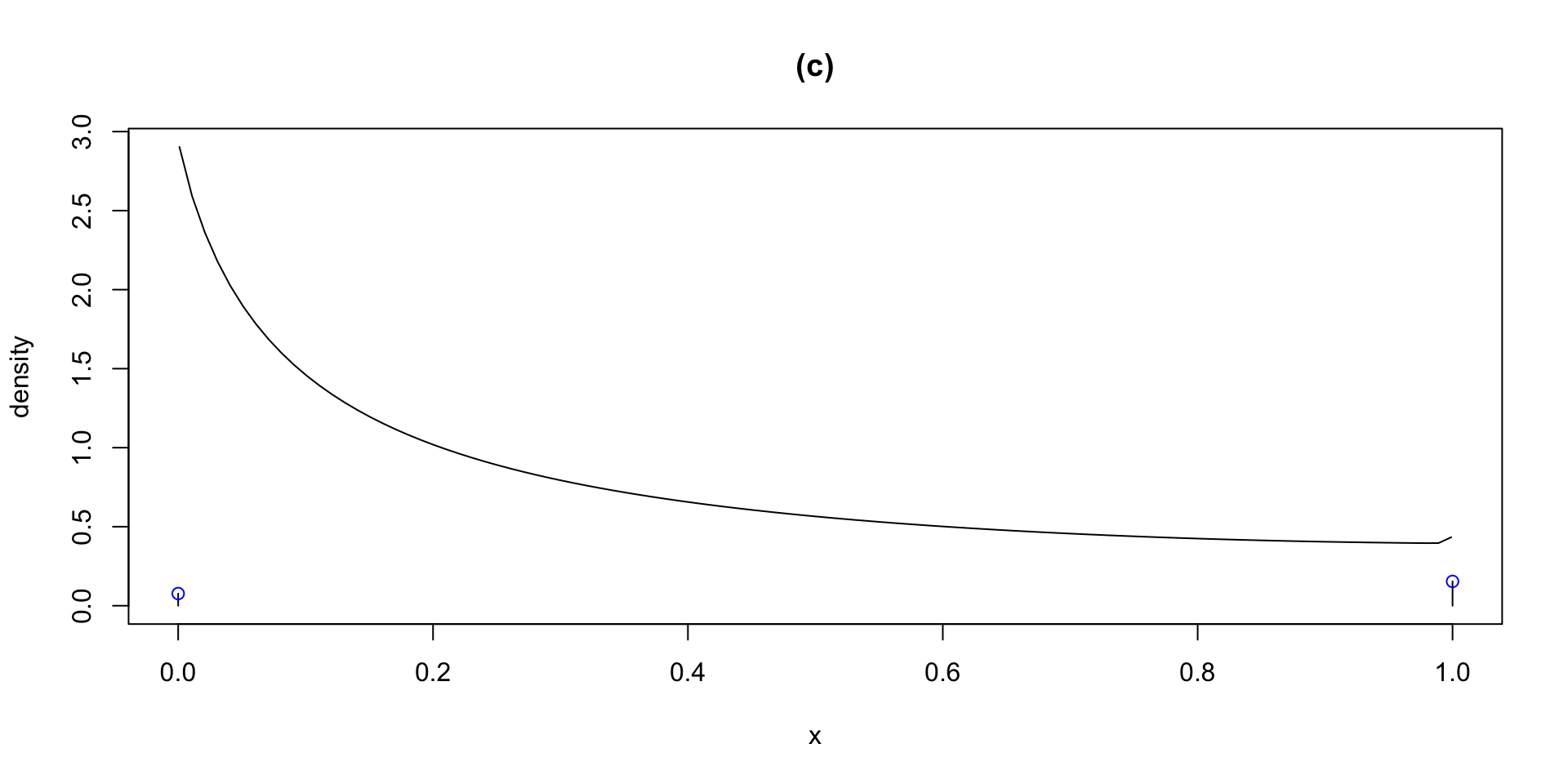
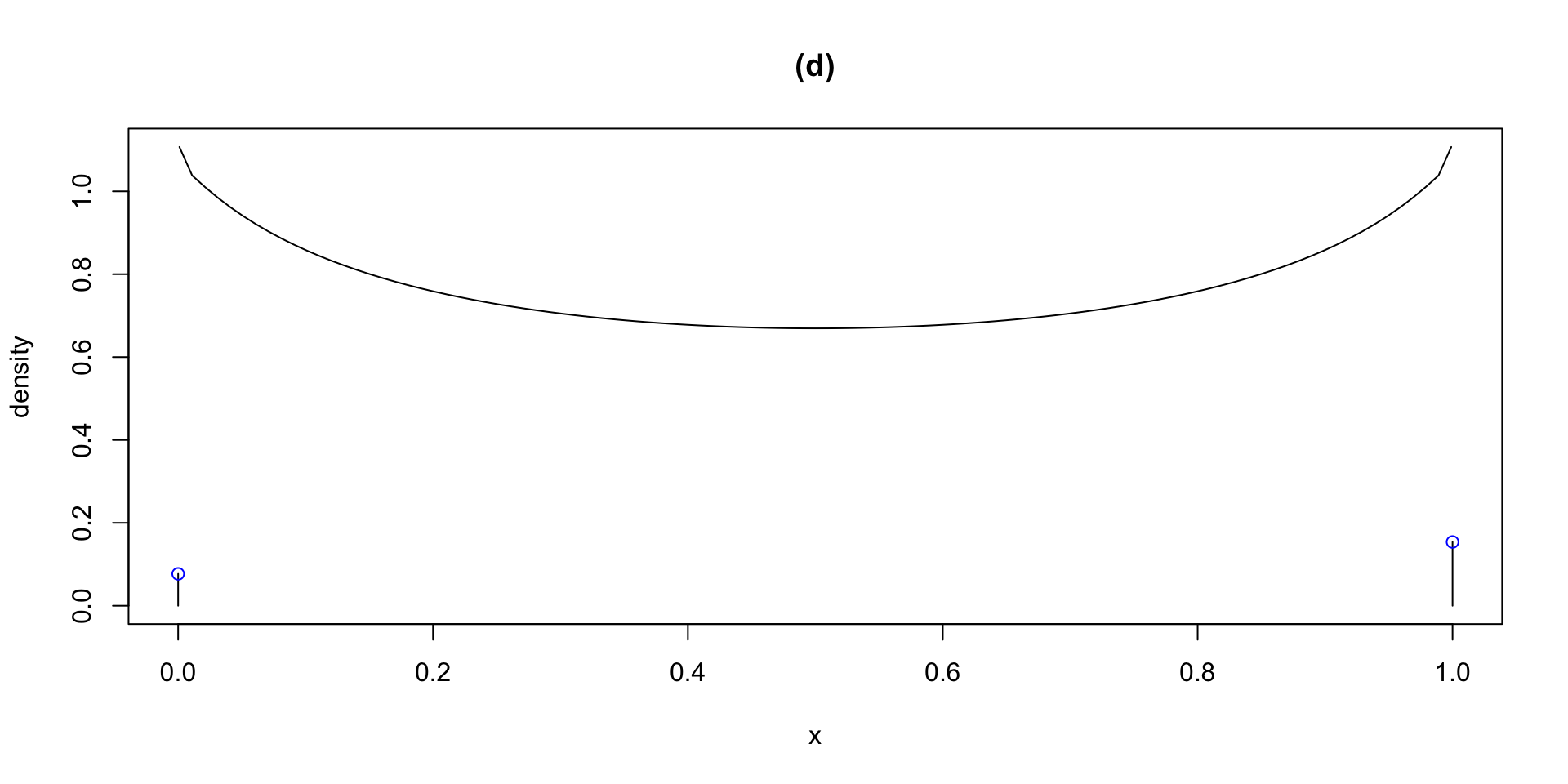
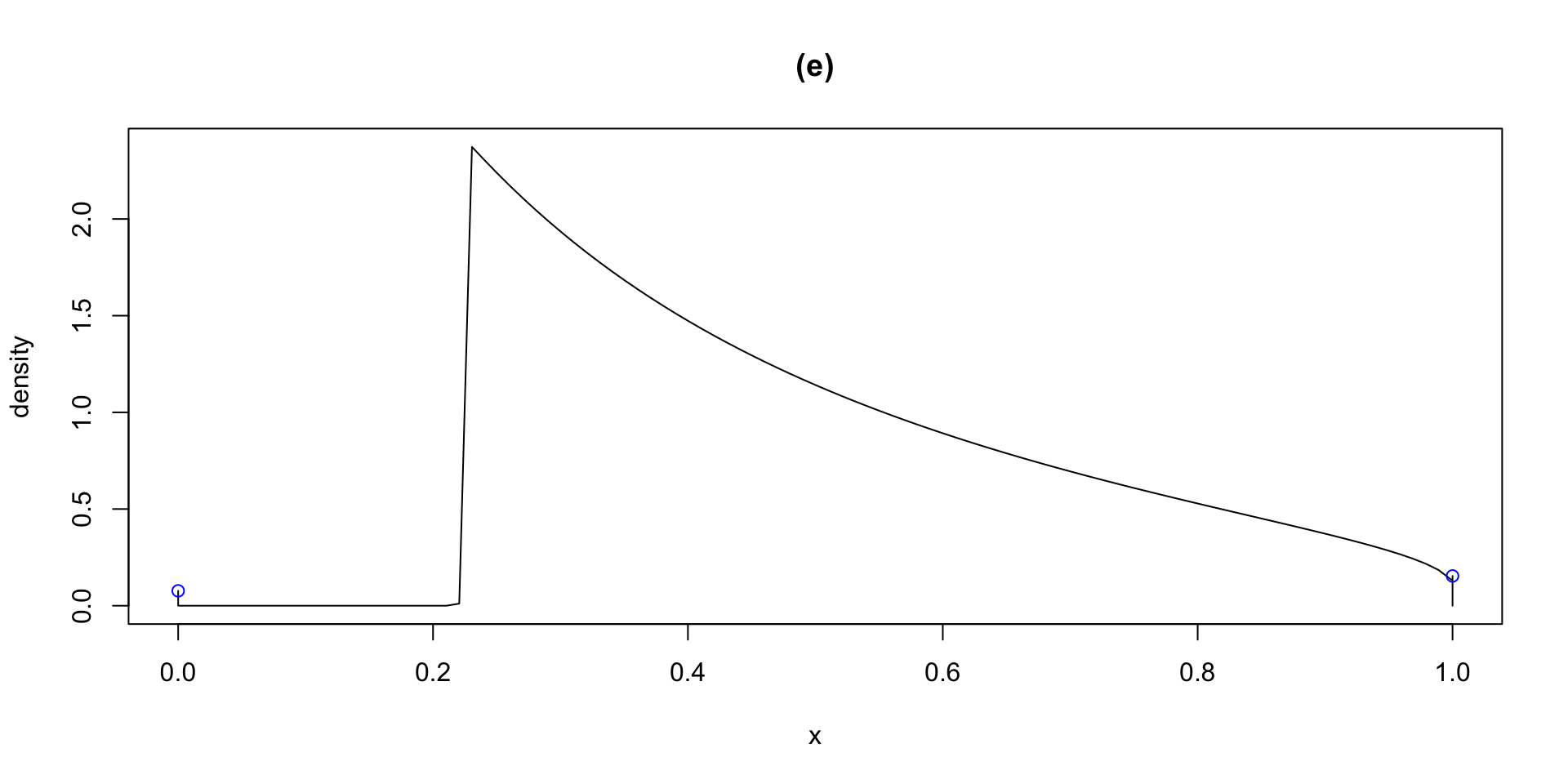
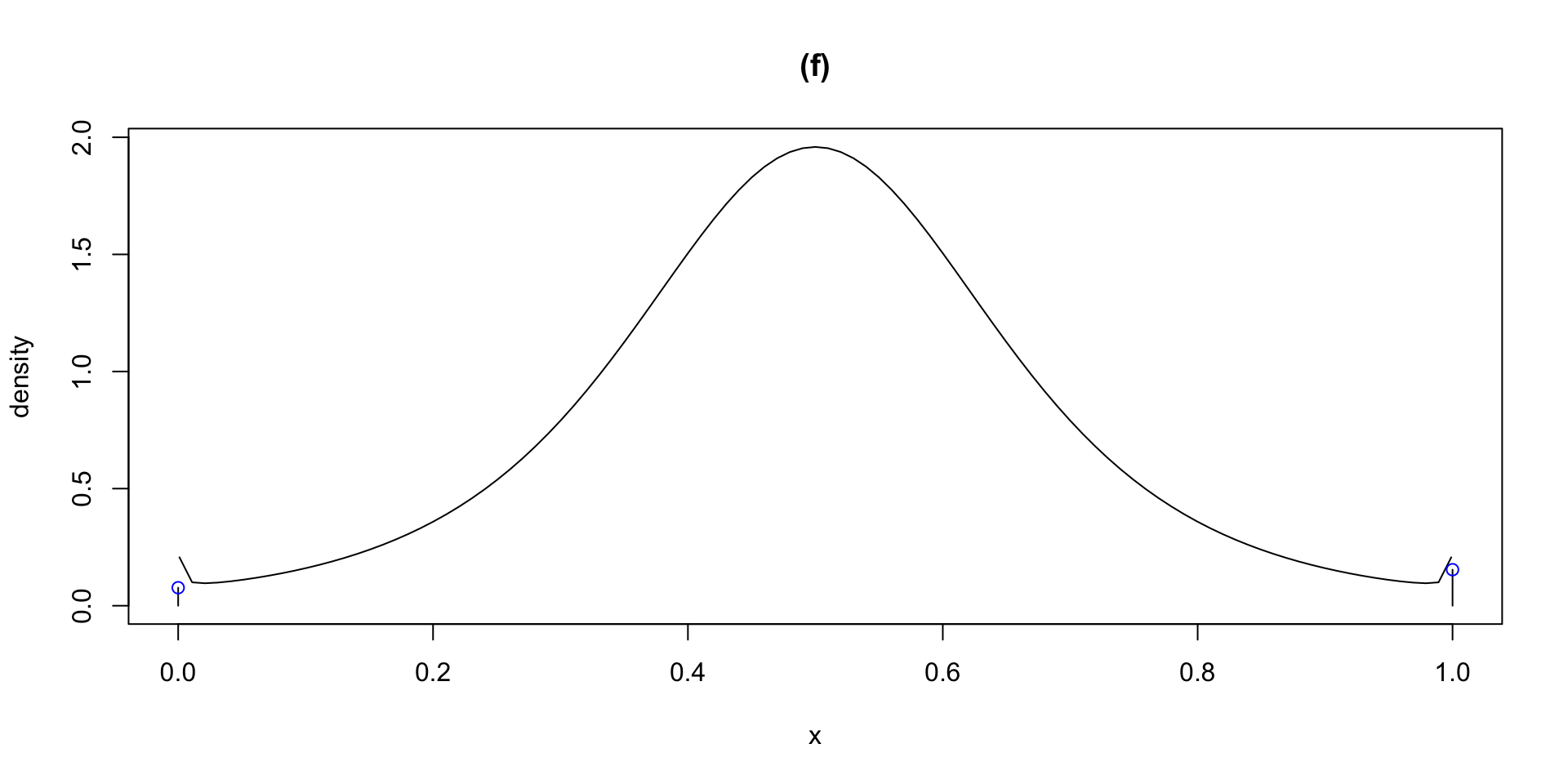
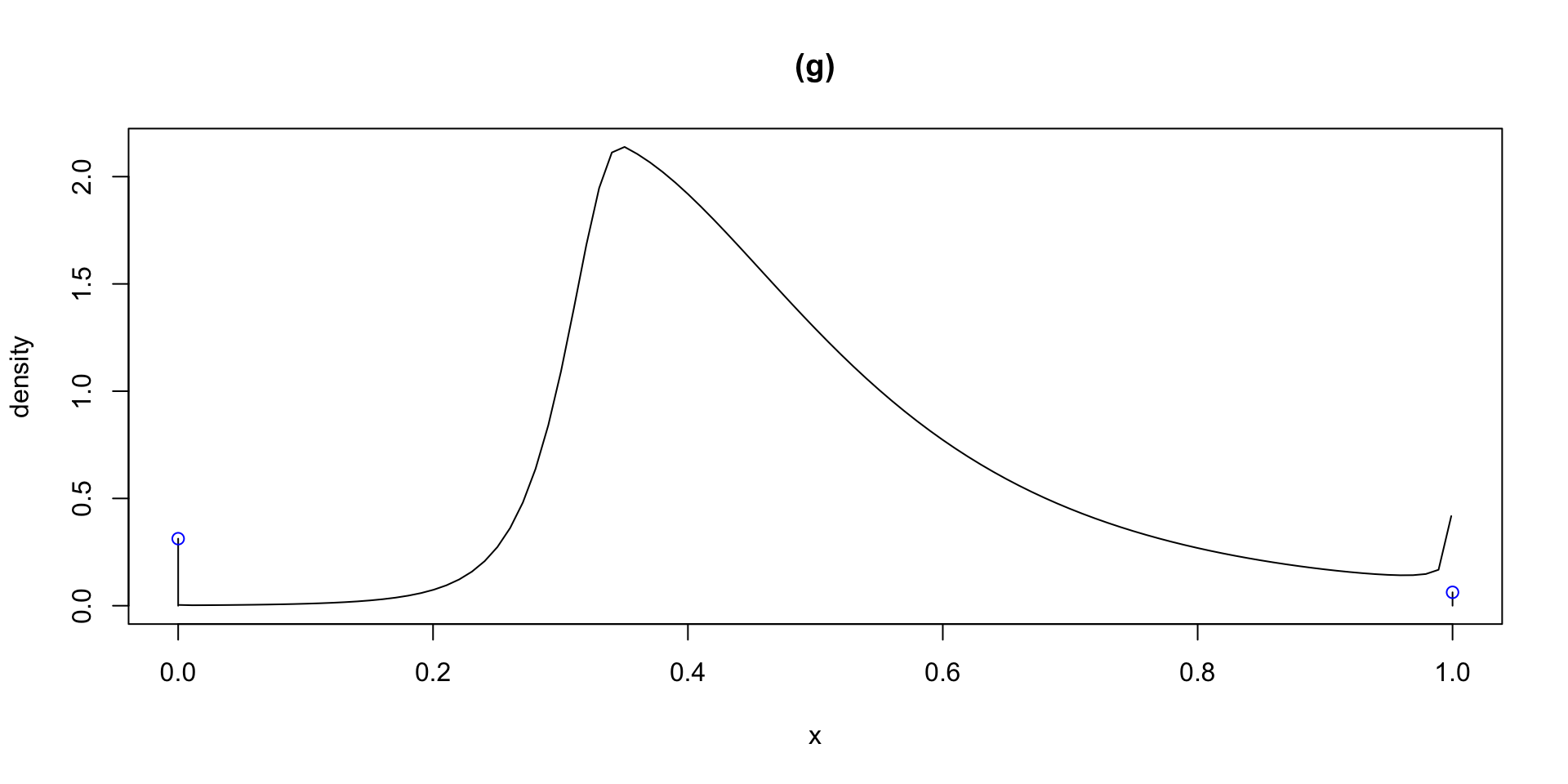
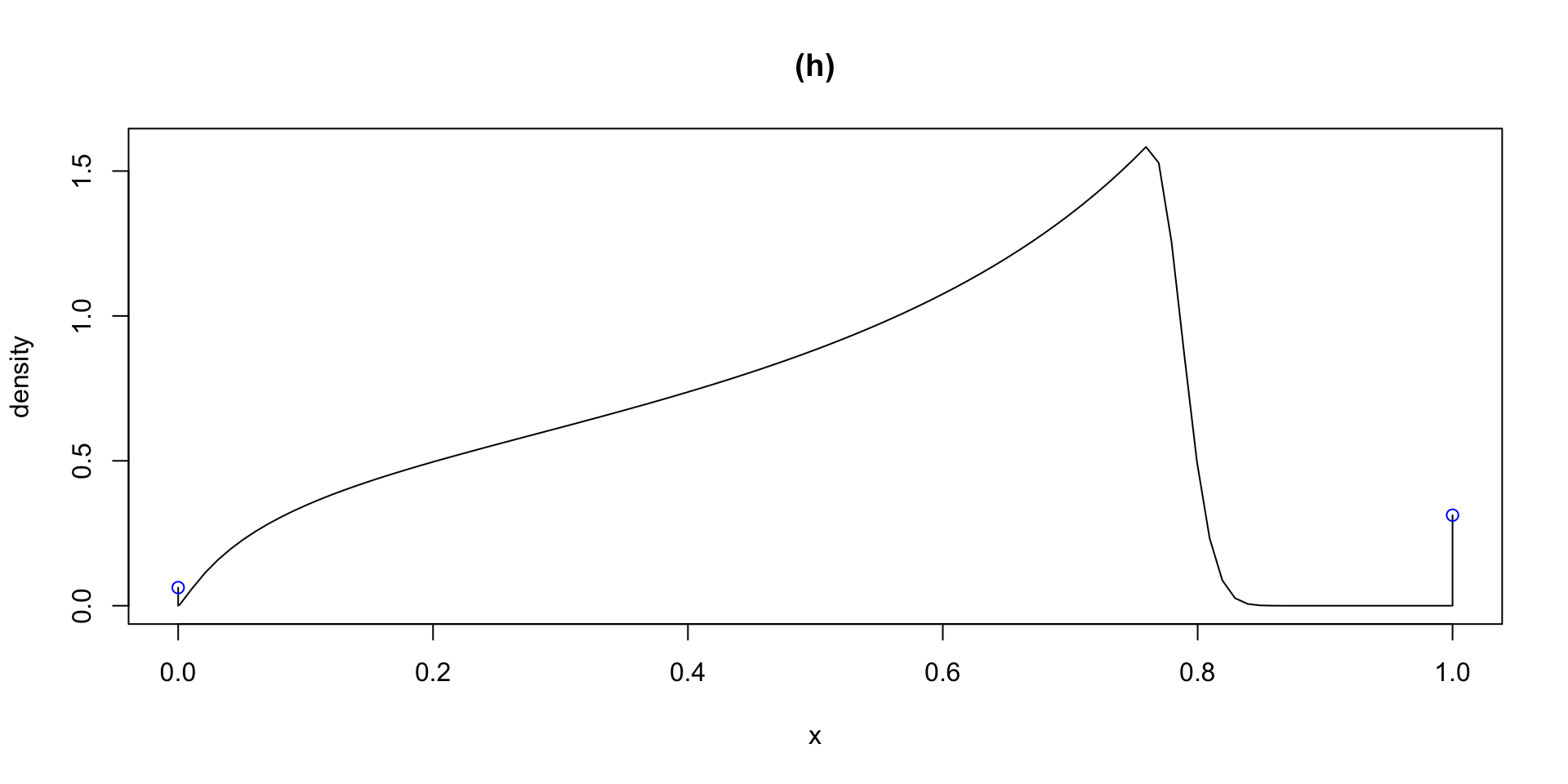
dlogSSTZadj plogSSTZadj qlogSSTZadj rlogSSTZadj
plotlogSSTZadj 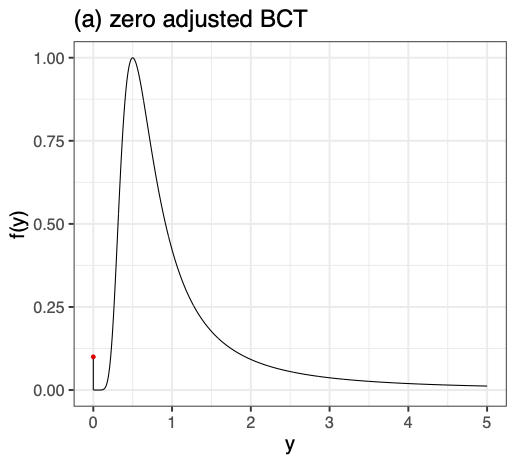
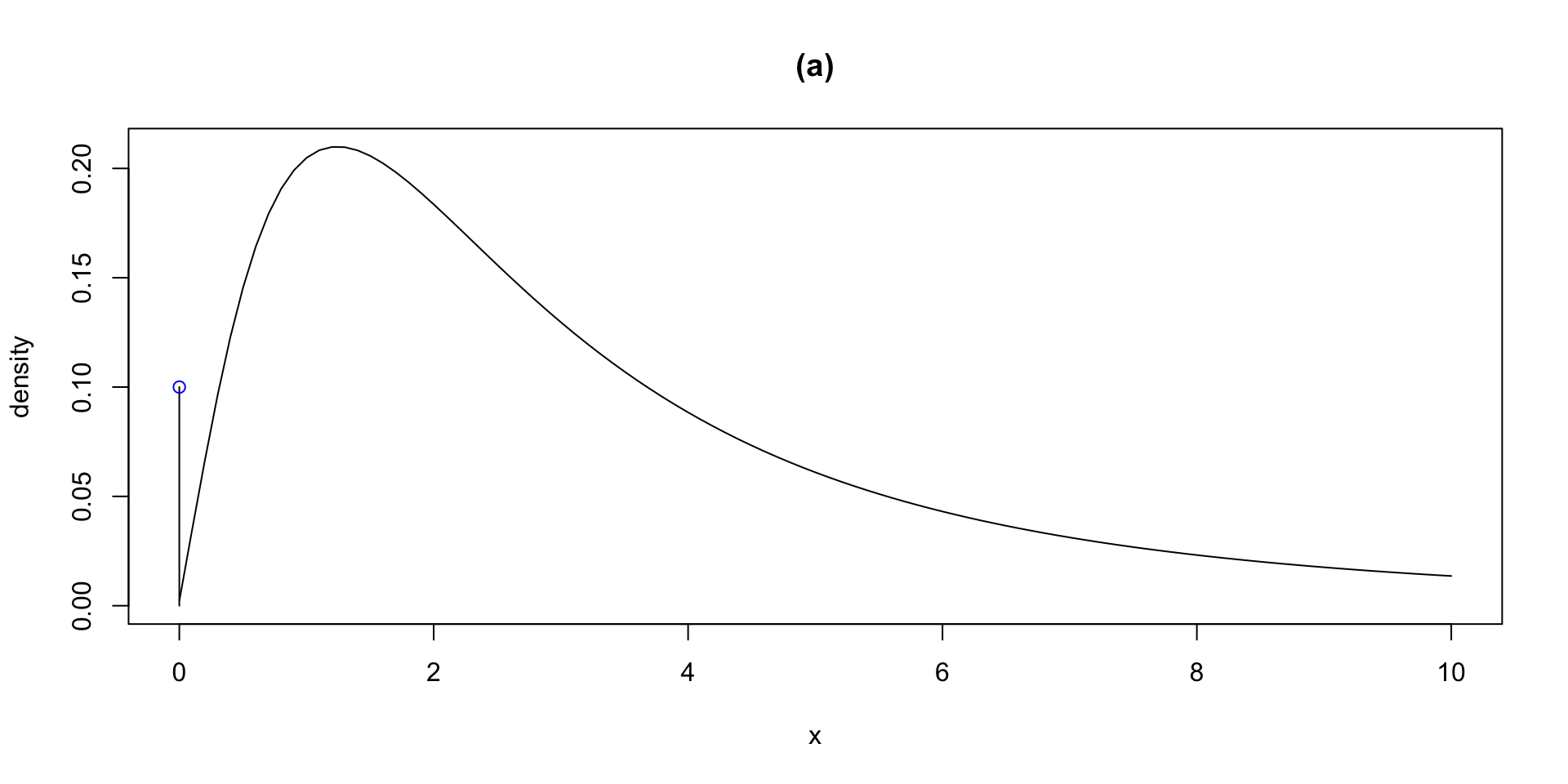
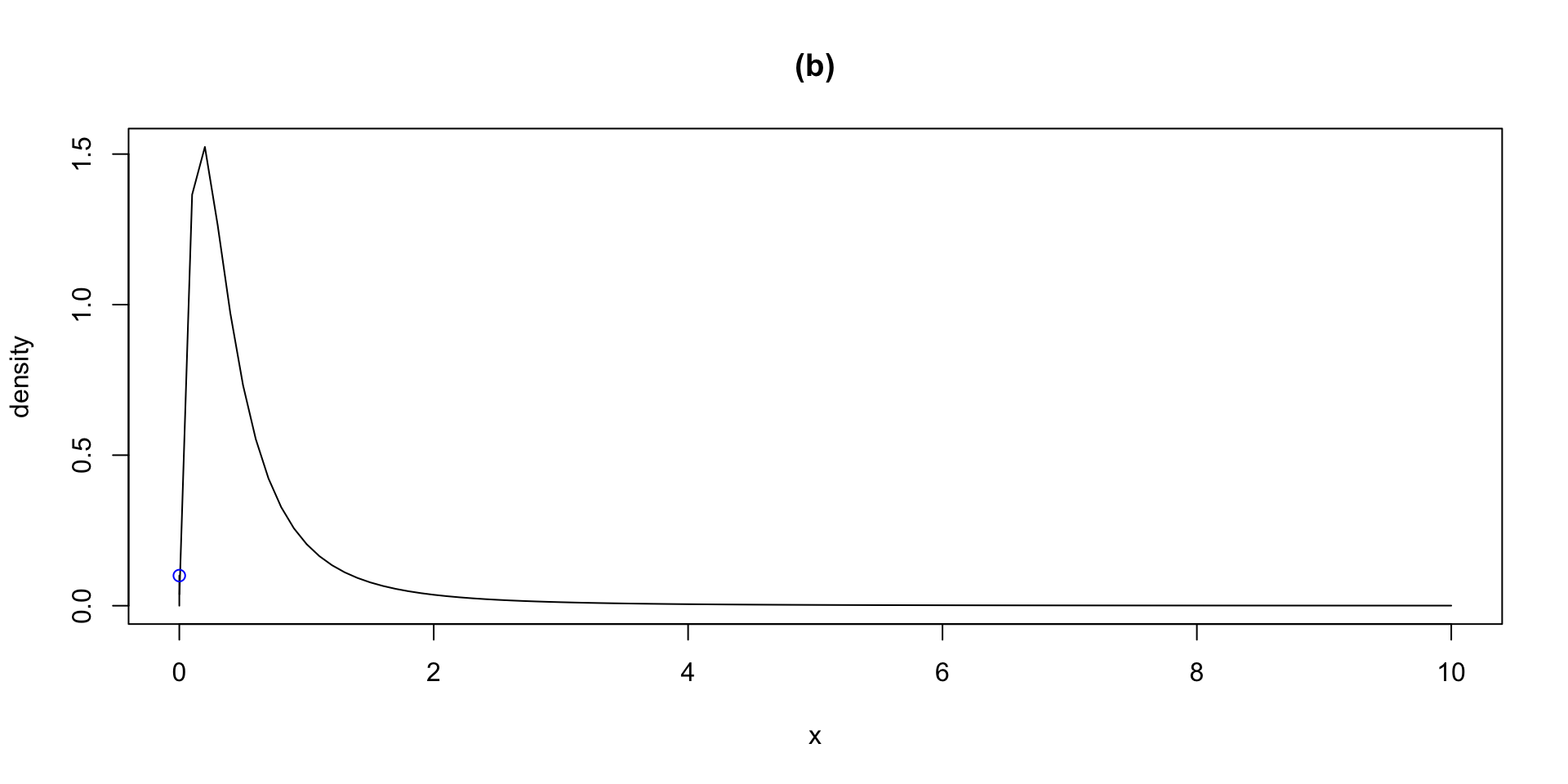
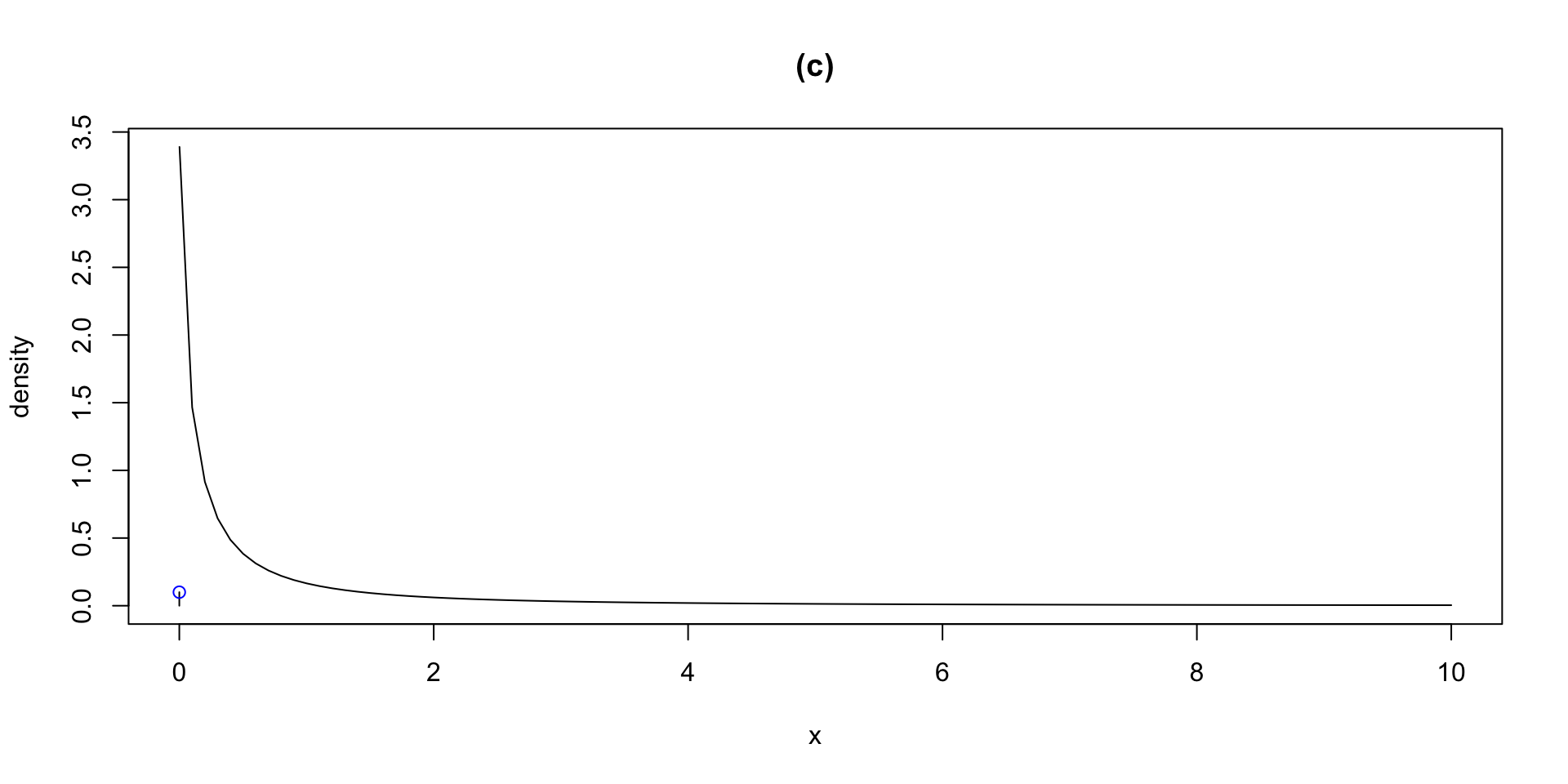


 The Books
The Books