flowchart TB A[Features.] --> B(Parameters) B --> D[Properties, \n Characteristics] D --> C(Distribution) B --> C
Interpreting models
Introduction
- how to interpreted
the effect of a single terminto the distribution of the response; - how to use the GAMLSS model for
prediction.
Interpretation
- how the information we obtain from the fitted model can be used
graphical Partial effects
ceteris paribus(concentate in one term fixing the rest)\(\textbf{x}_j\) denote a single (or maximum two terms)
\(\textbf{x}_{-j}\) all the rest so \(\{\textbf{x}_j, \textbf{x}_{-j} \}\) are all terms in the model
\(\omega(D)\) the characteristic of the distribution we are interested \({D}(y | \textbf{x}_j , \textbf{x}_{-j}; \boldsymbol{\theta})\) i.e. kurtosis
under scenario, \(\textbf{S}[g()]\) ()
\[{PE}_{\omega({D})}\left( \textbf{x}_{j} | \textbf{S} \left[ g(\textbf{x}_{-j})\right] \right)\]
Scenarios
fixingvalues of \(\textbf{x}_{-j}\) (mean or median for continuous, level with more number of observations for factors or other possible values of importance)averageover values of \(\textbf{x}_{-j}\)Partial Dependence Plots(PDF), \(\textbf{S}\left[ \text{average}(\textbf{x}_{-j})\right]\)
Accumulated Local Effects, (ALE), accumulated average local differencesMarginal Effects(ME) average over local neighbourhood
Characteristics
predictors, \(\eta_{\theta_i}\)parameters, \(\theta_i\)moment, i.e. mean and variancequantilesi.e. mediandistribution
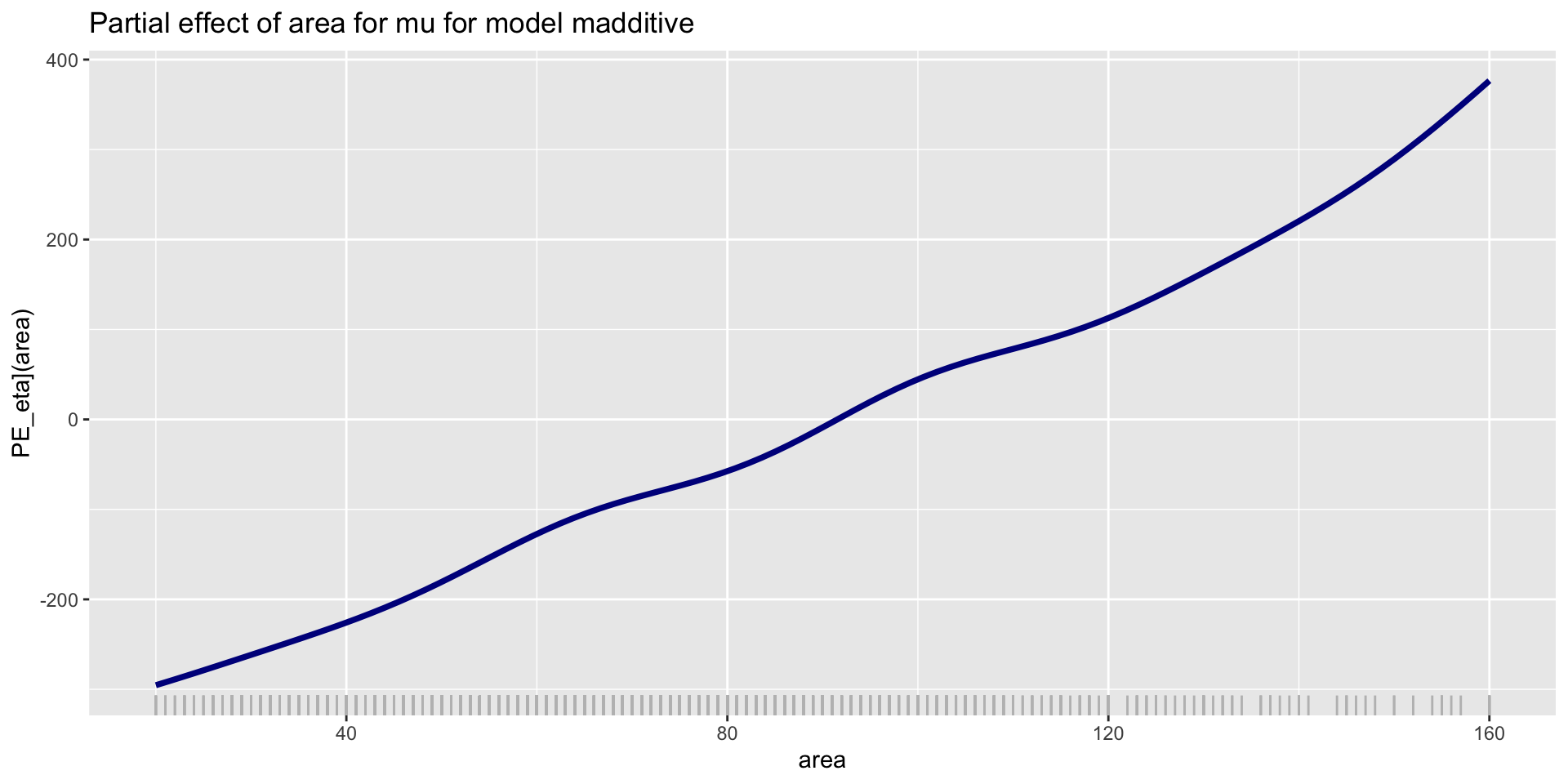
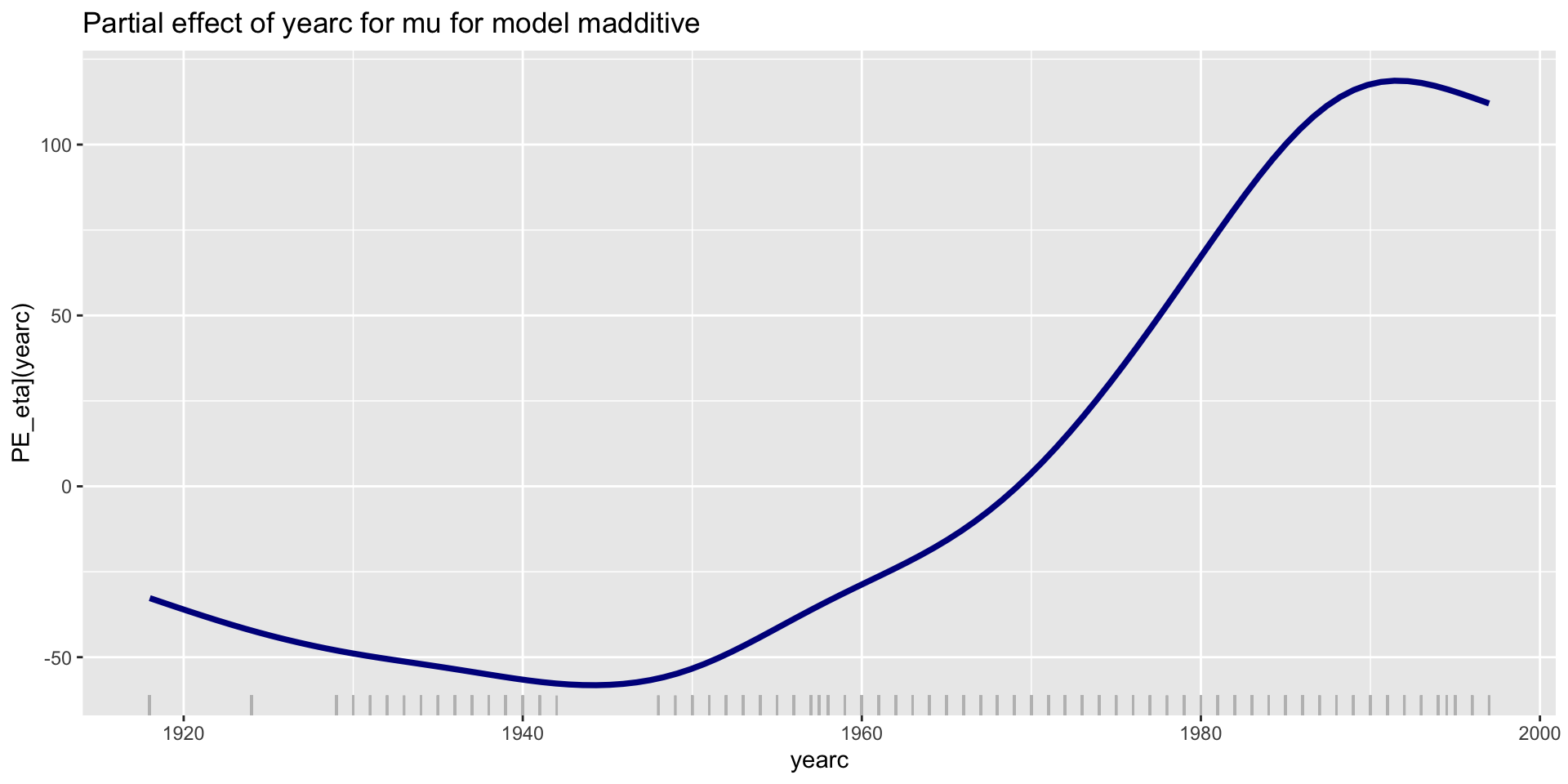
PE-parameter \(\mu\) additive
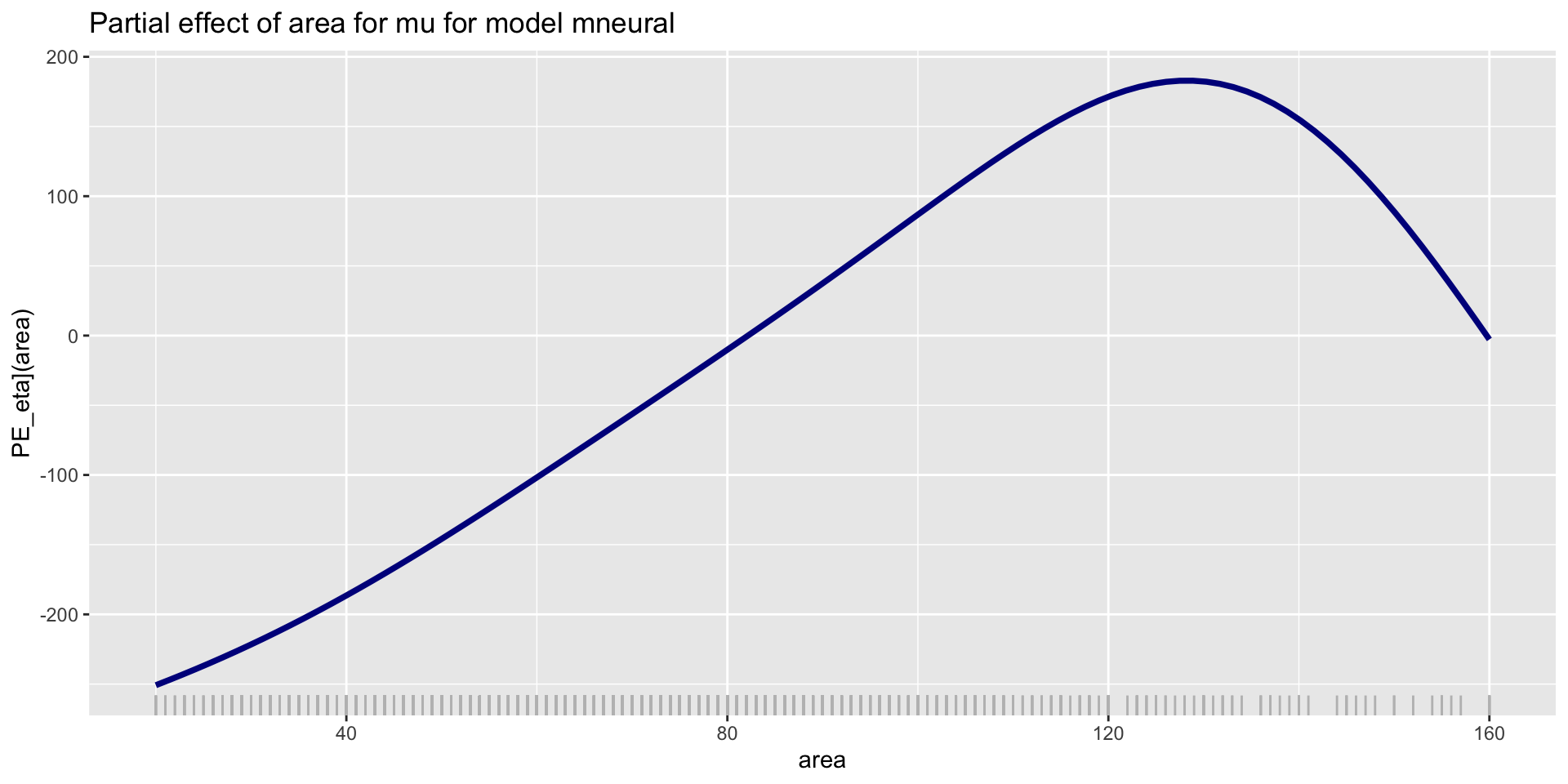
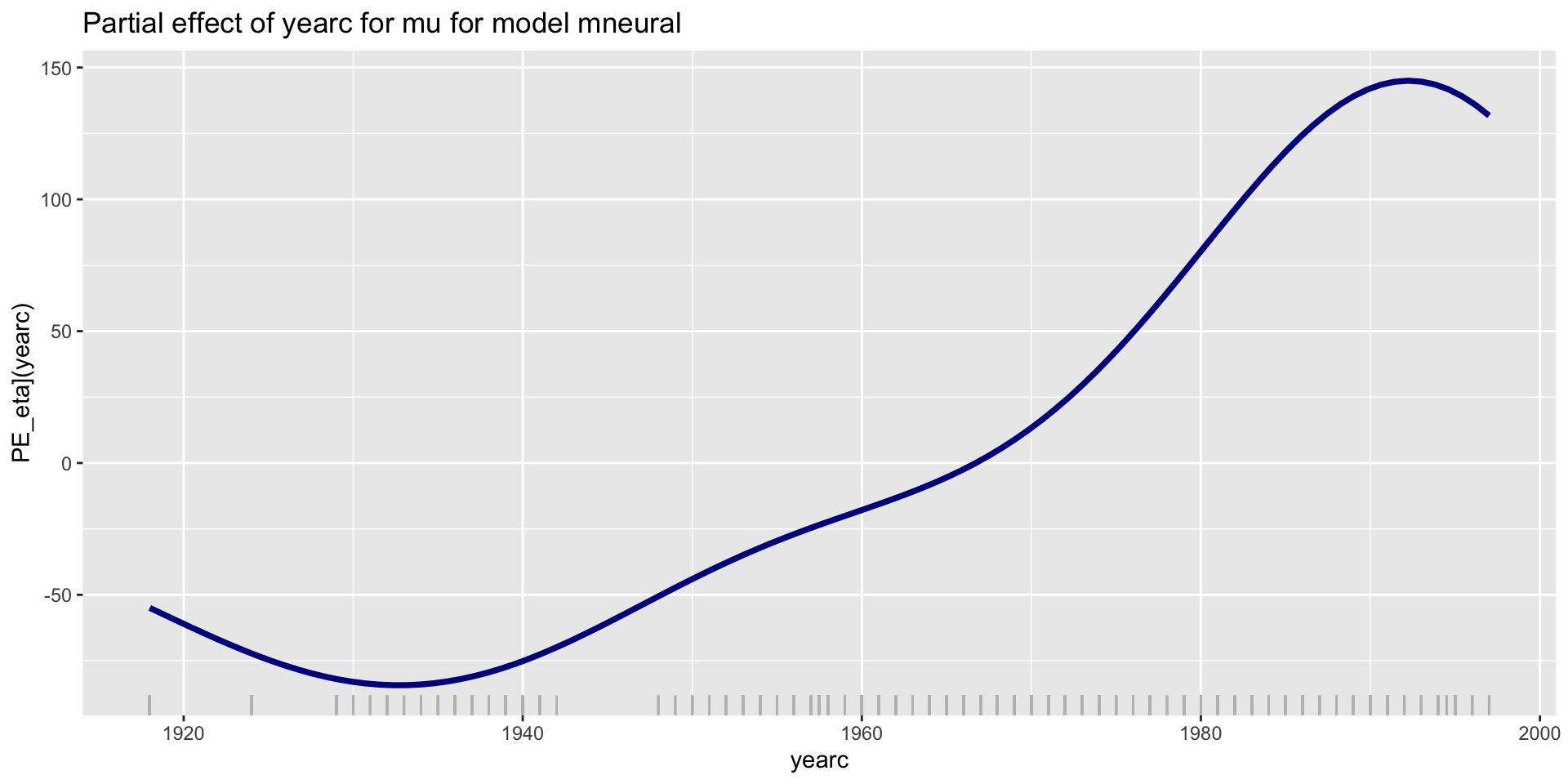
PE-parameter \(\mu\) NN
PE; parameter \(\sigma\); additive
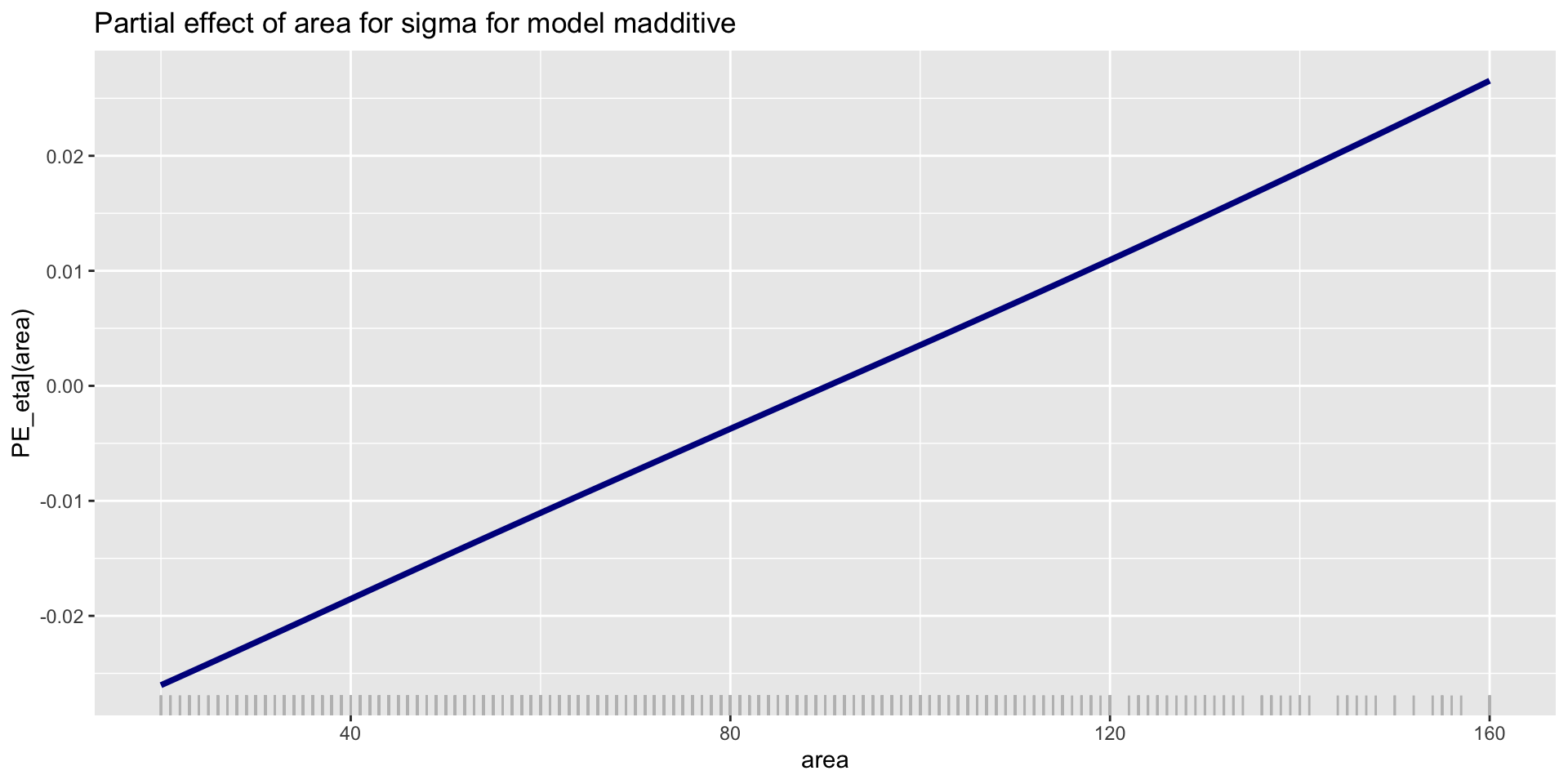
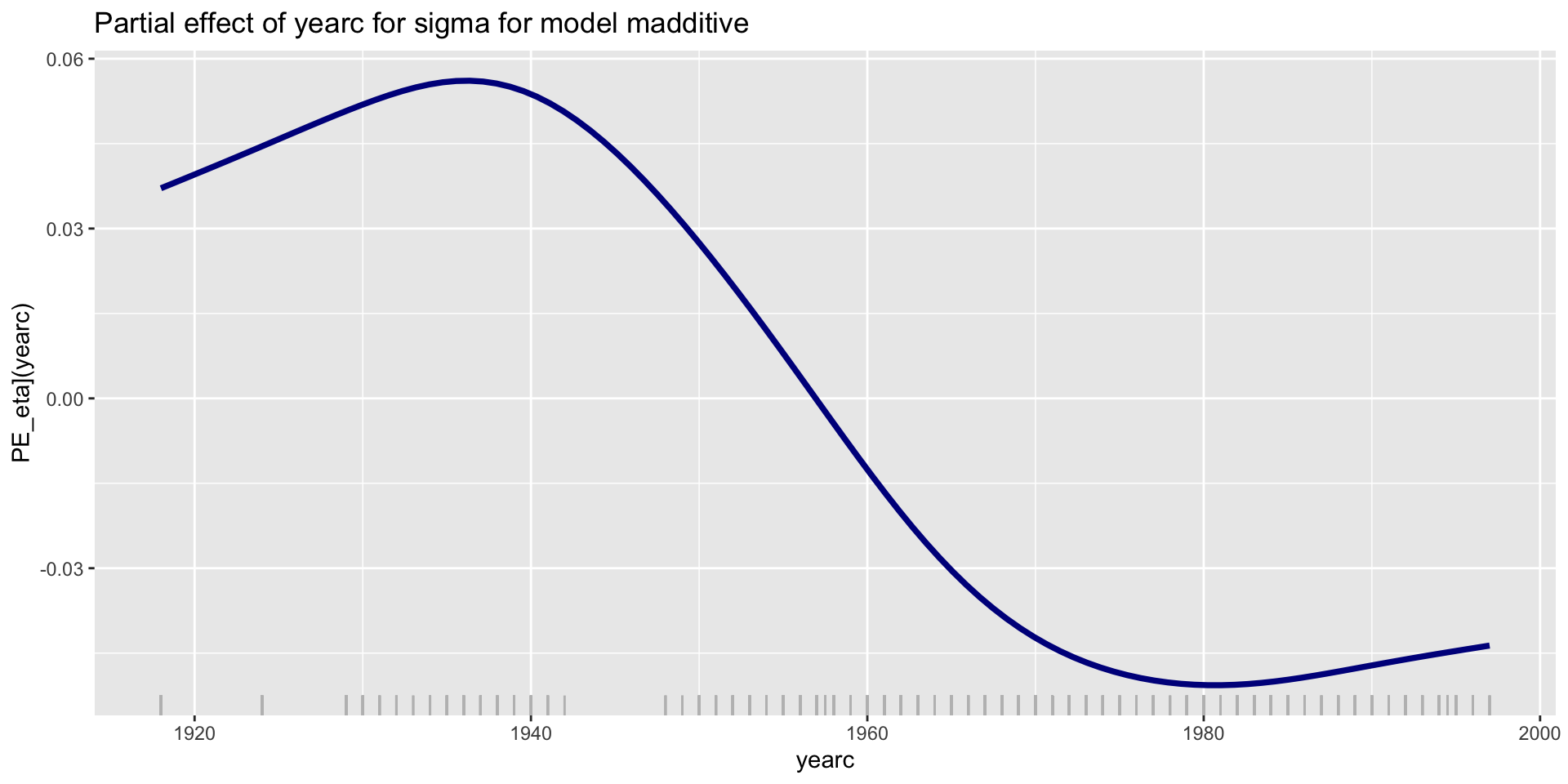
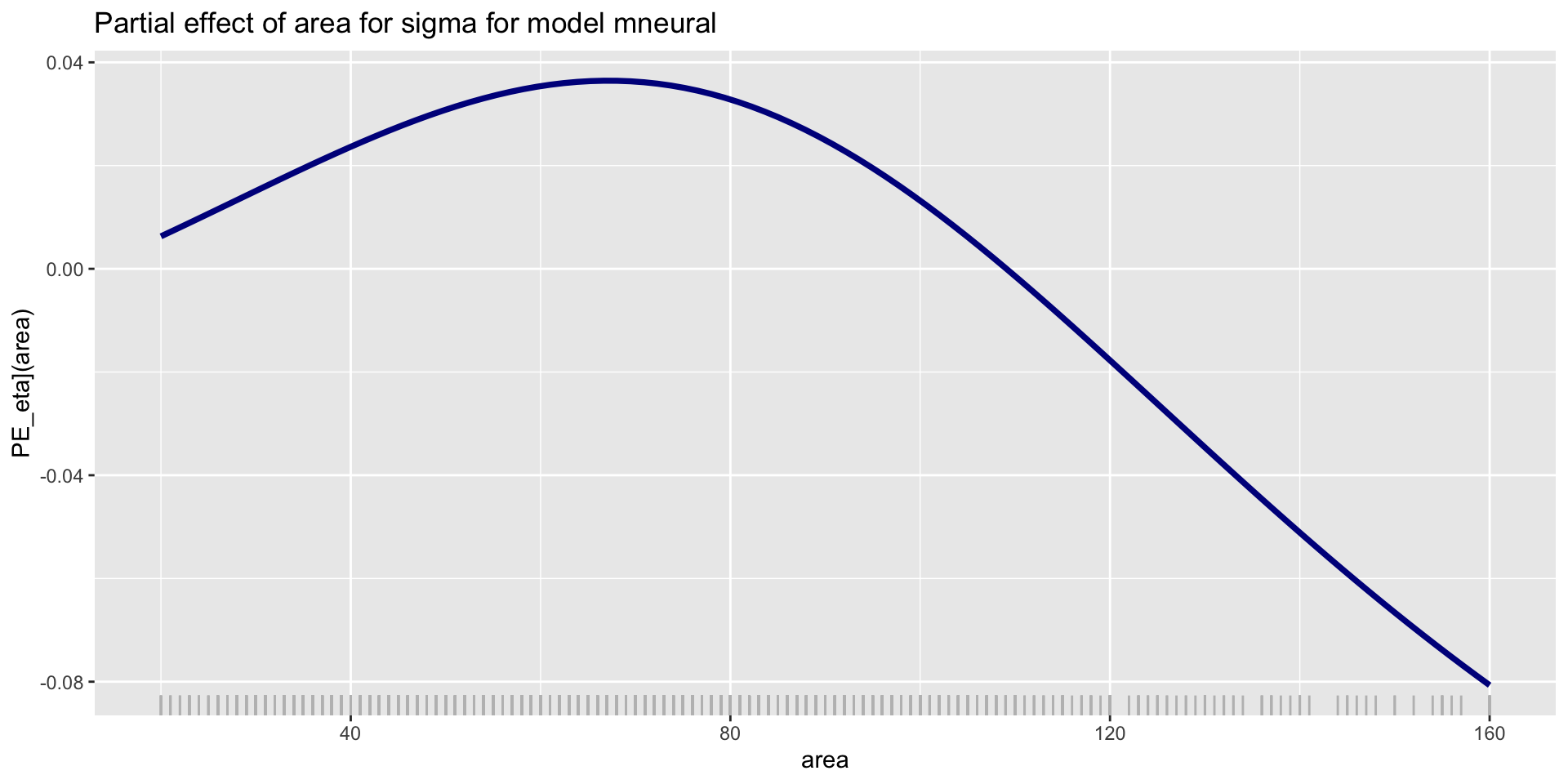
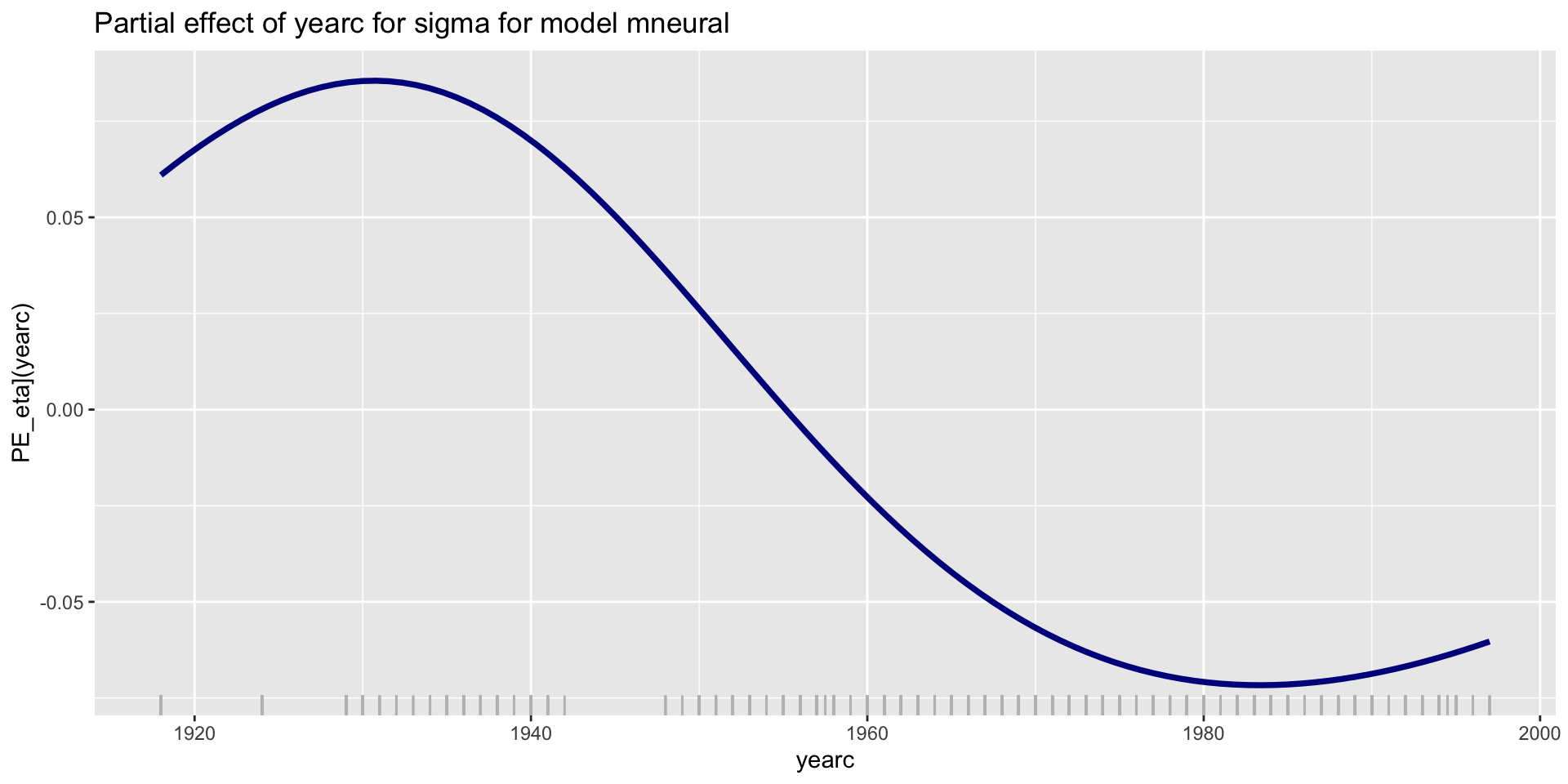
PE; parameter \(\sigma\); NN
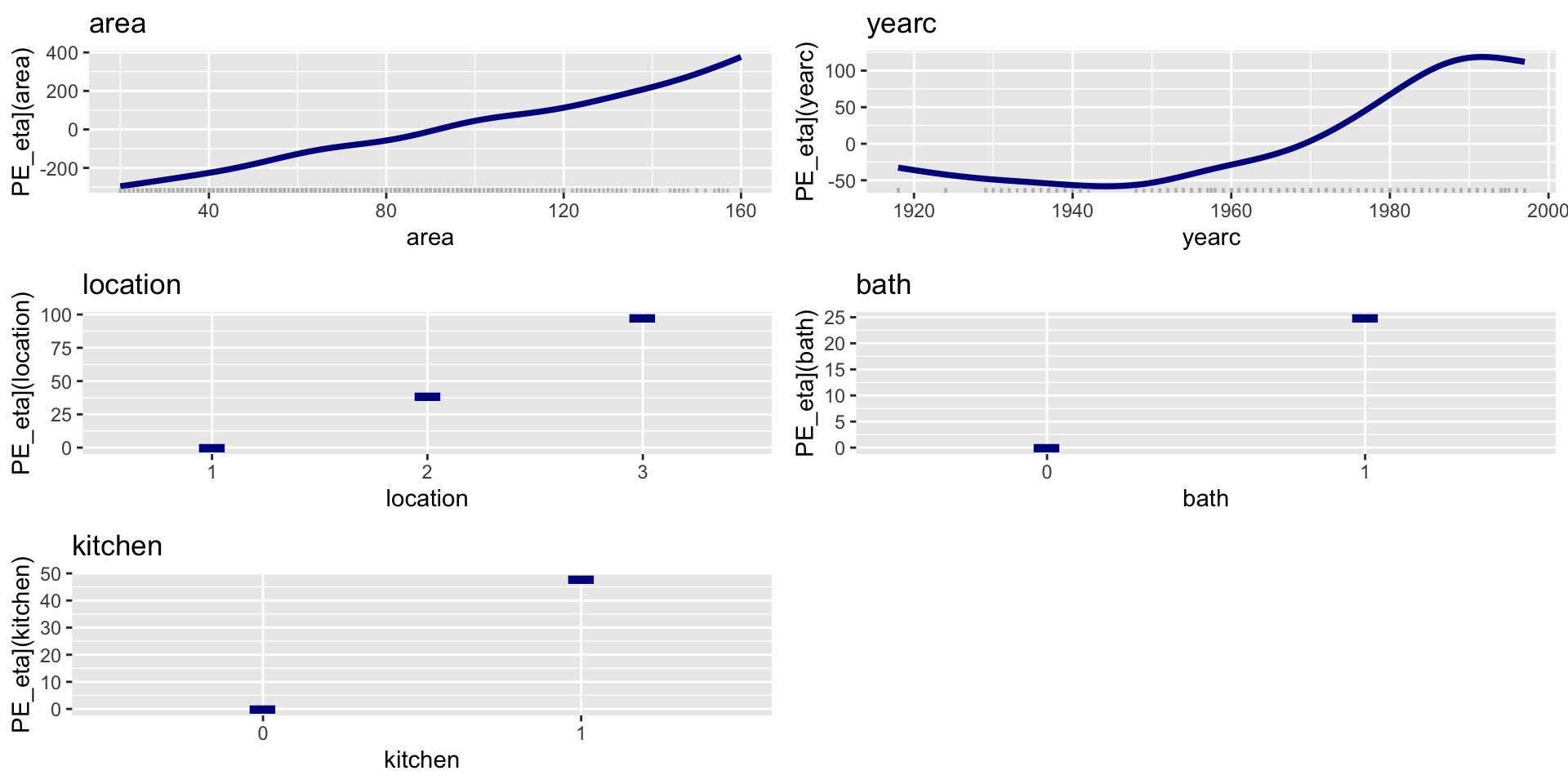
all terms (additive)
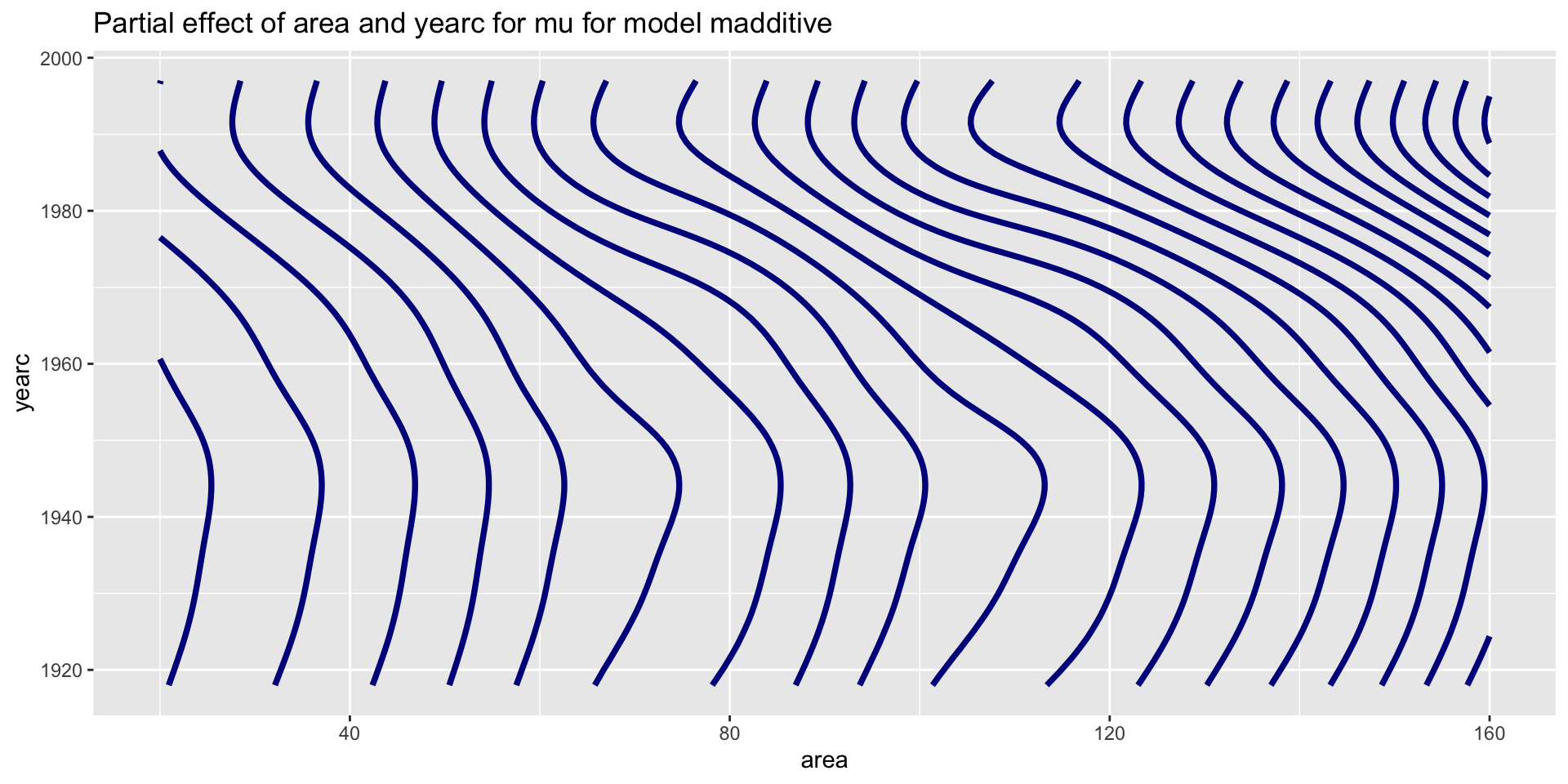
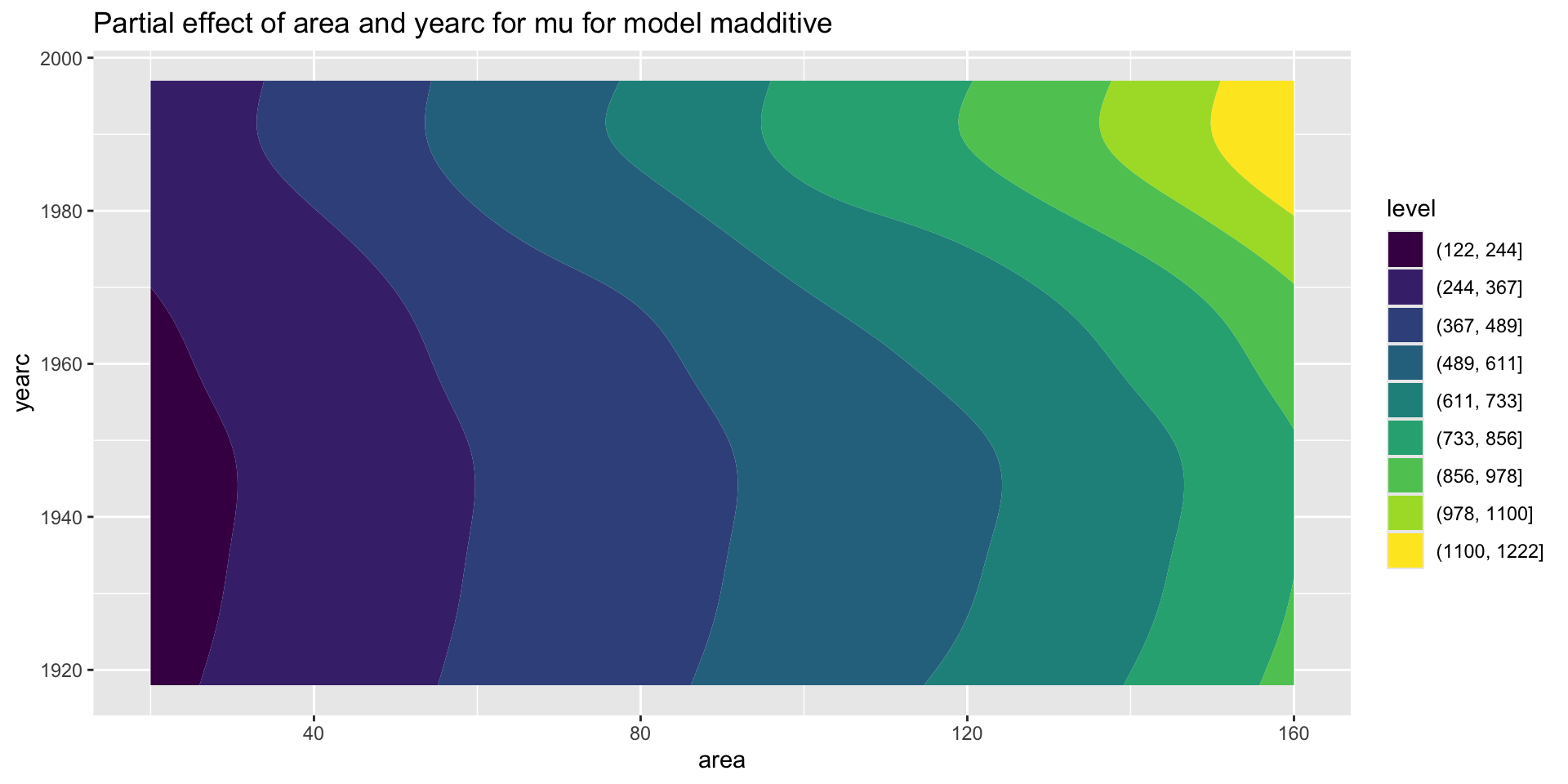
2 way interactions (additive)
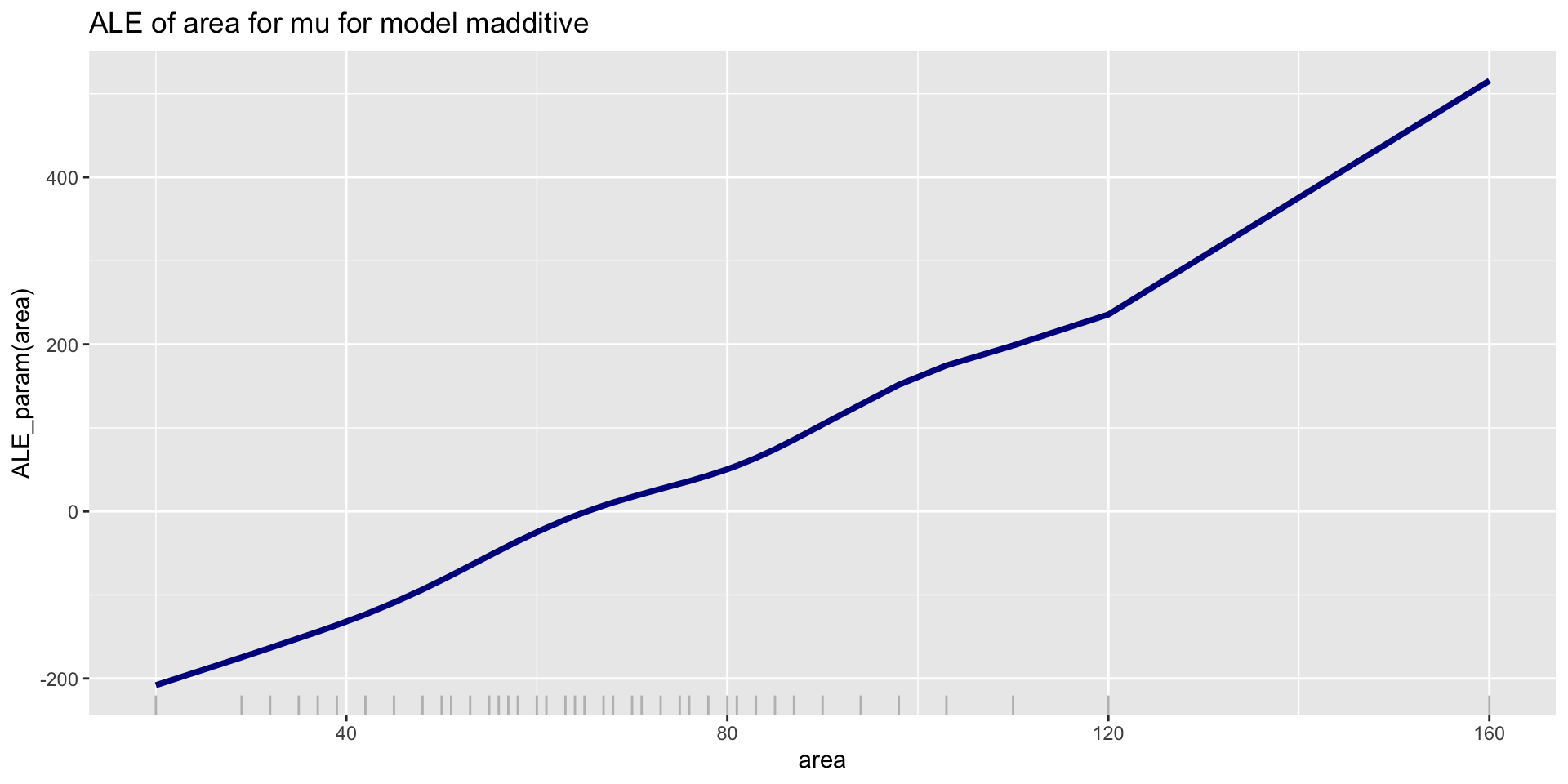
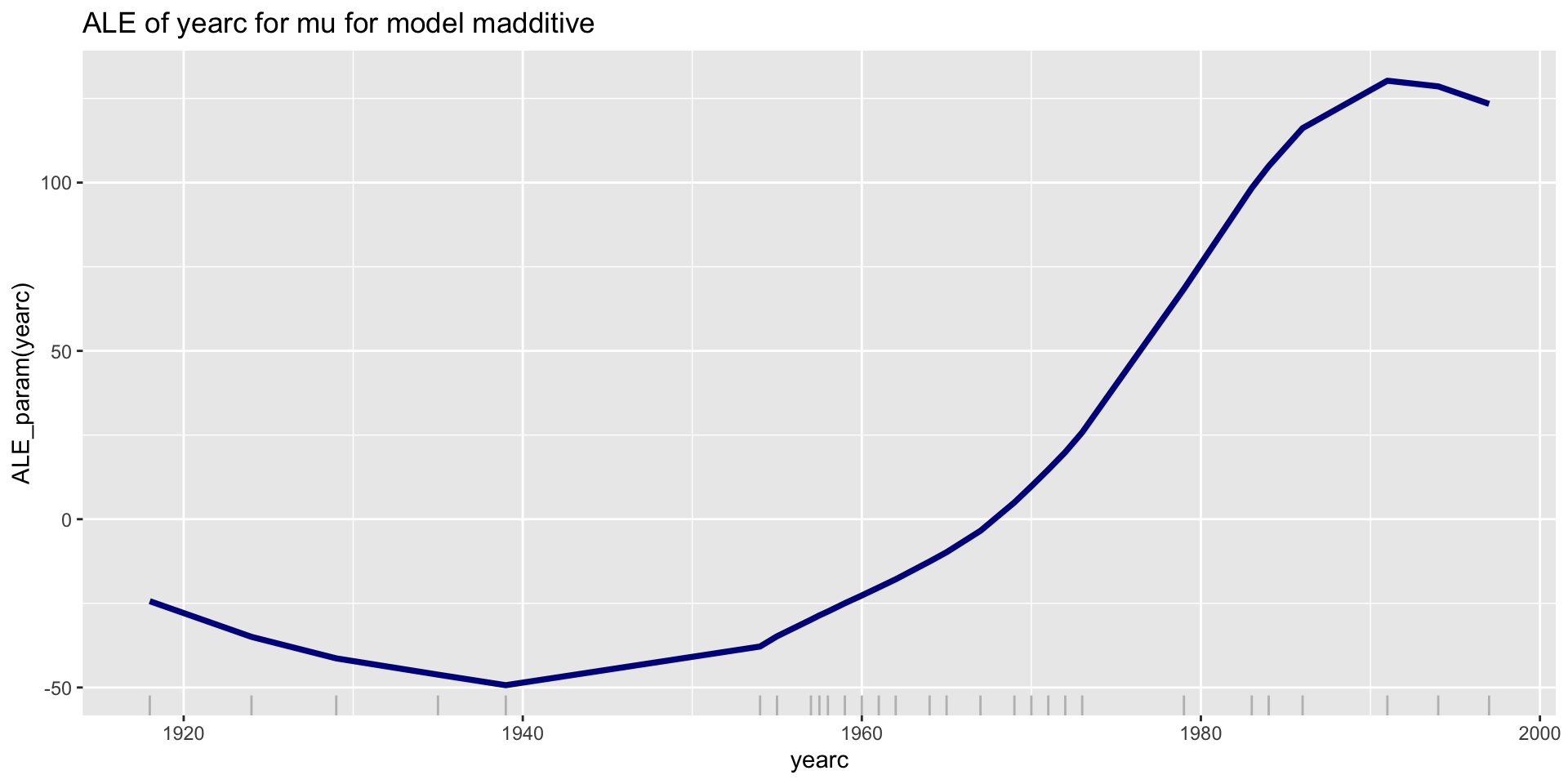
ALE; parameters \(\mu\); Additive
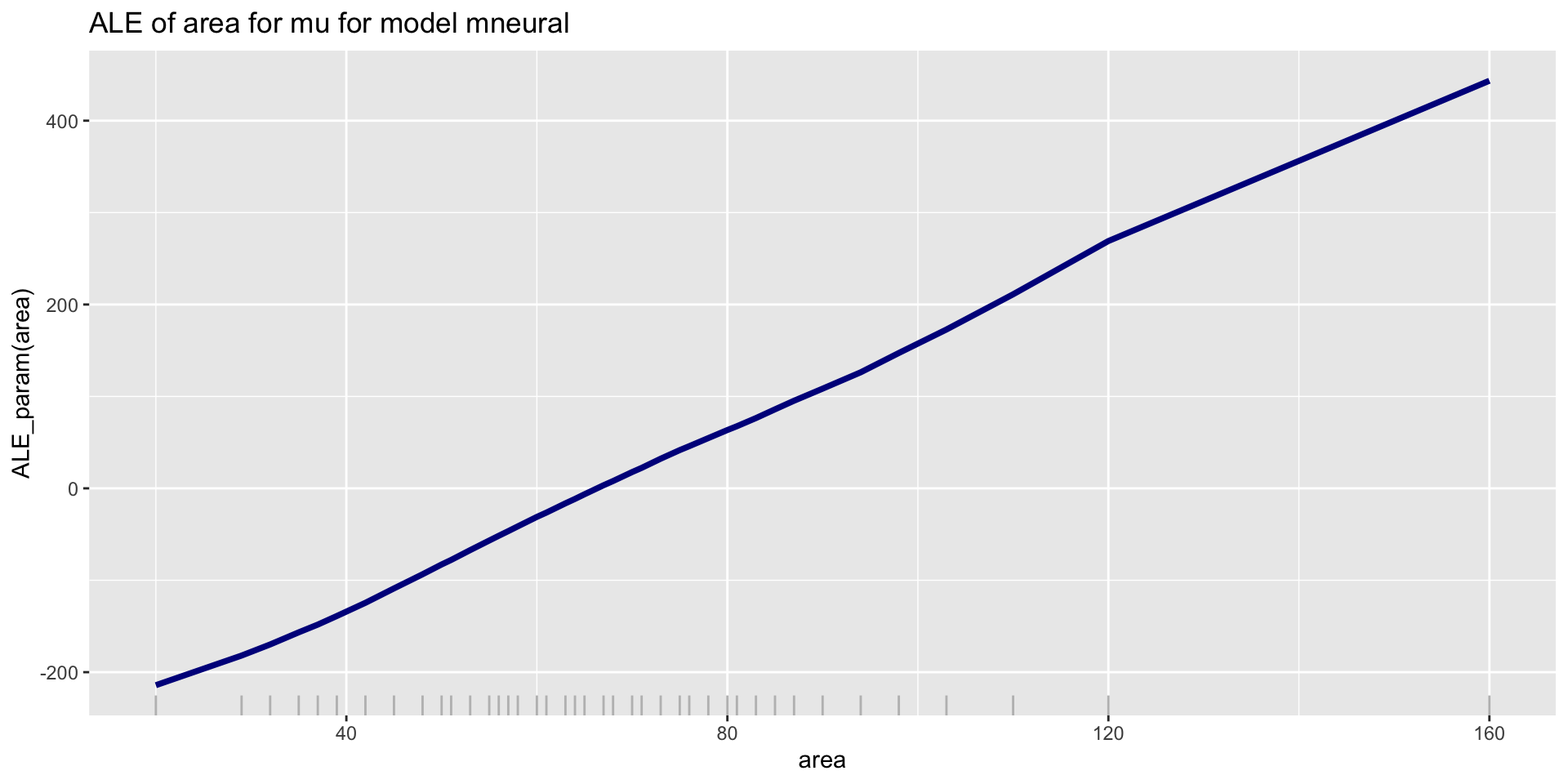
ALE; parameters \(\mu\); NN

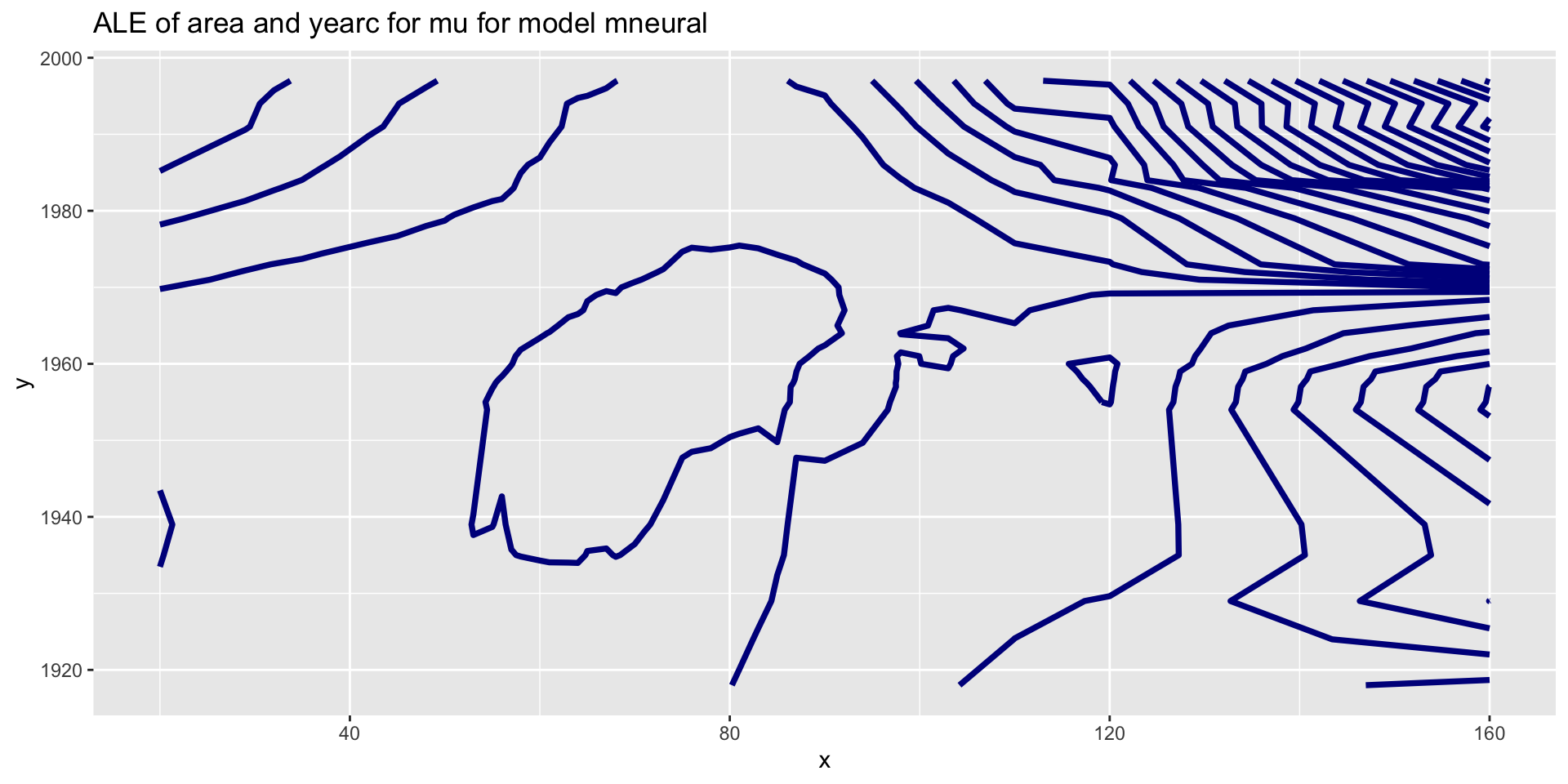
ALE interactions
gamlss.ggplots:::ale_param(madditive,c("area", "yearc"))
gamlss.ggplots:::ale_param(mneural,c("area", "yearc"))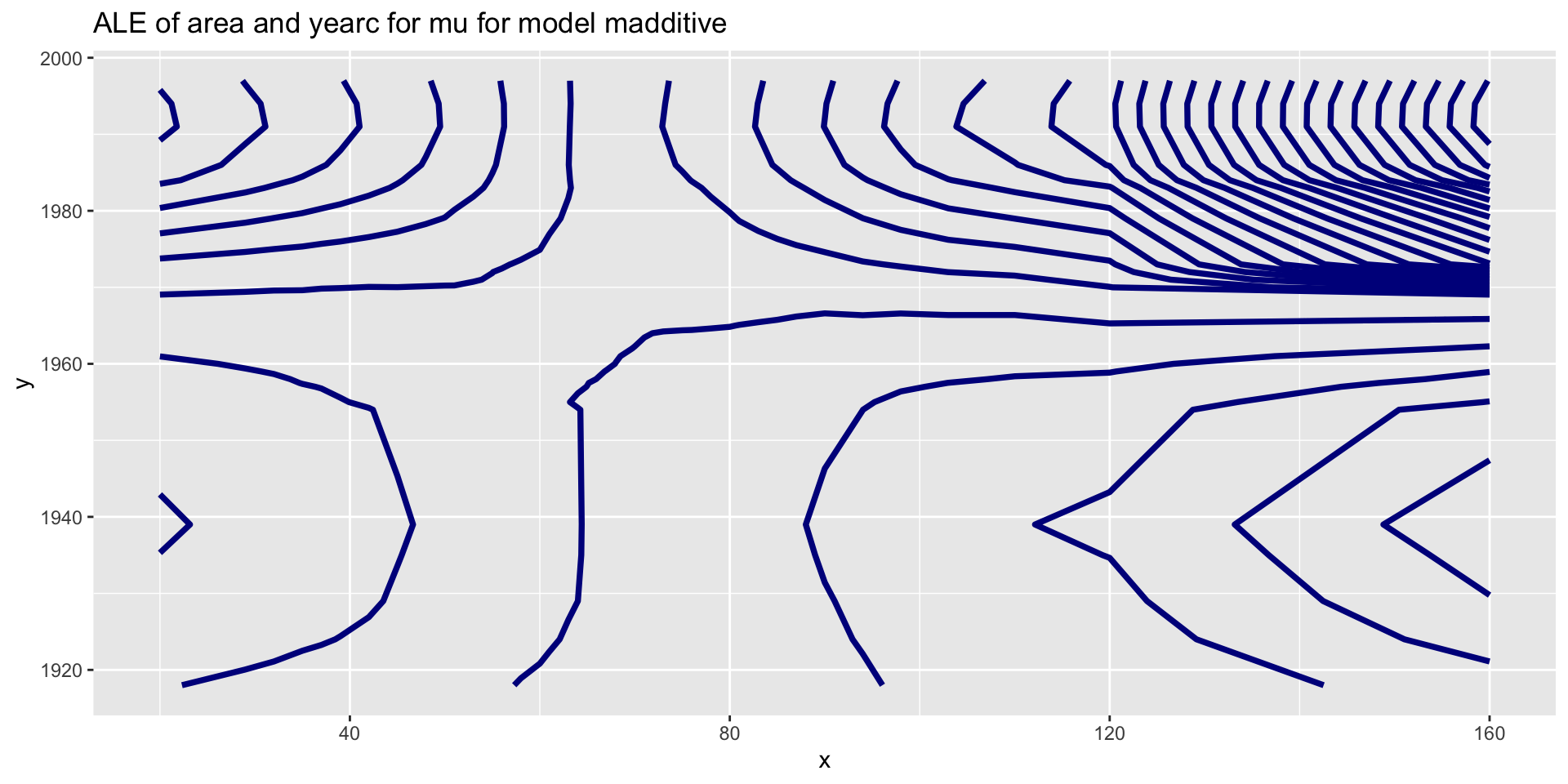
moments (mean)
Not implemented yet for
gamlss2objectsNote that moments not always exist for example for the
BCTodistributionfor \(\tau\le2\) the variance do not exist
for \(\tau\le1\) the mean do not exist
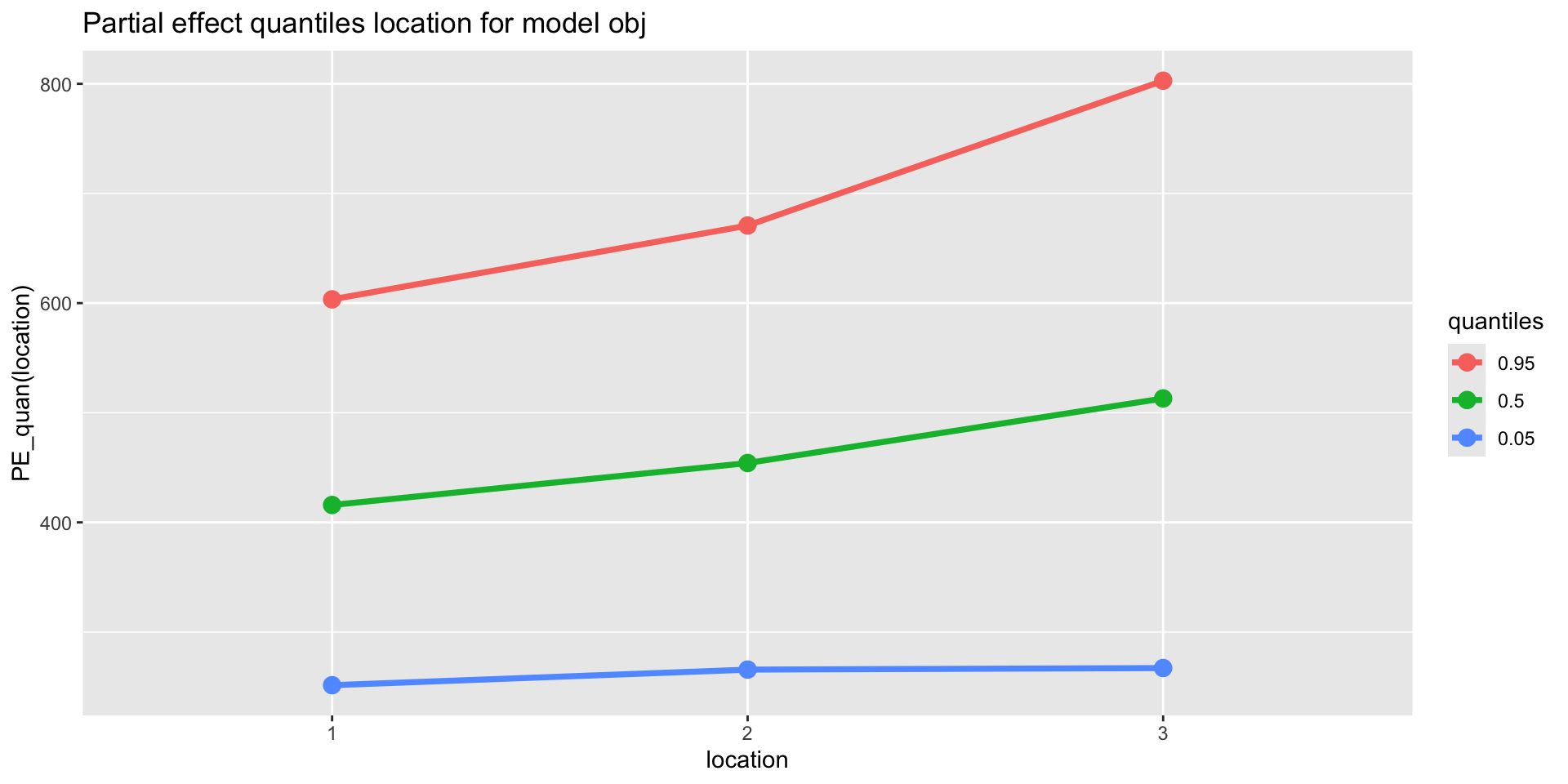
quantiles, additive
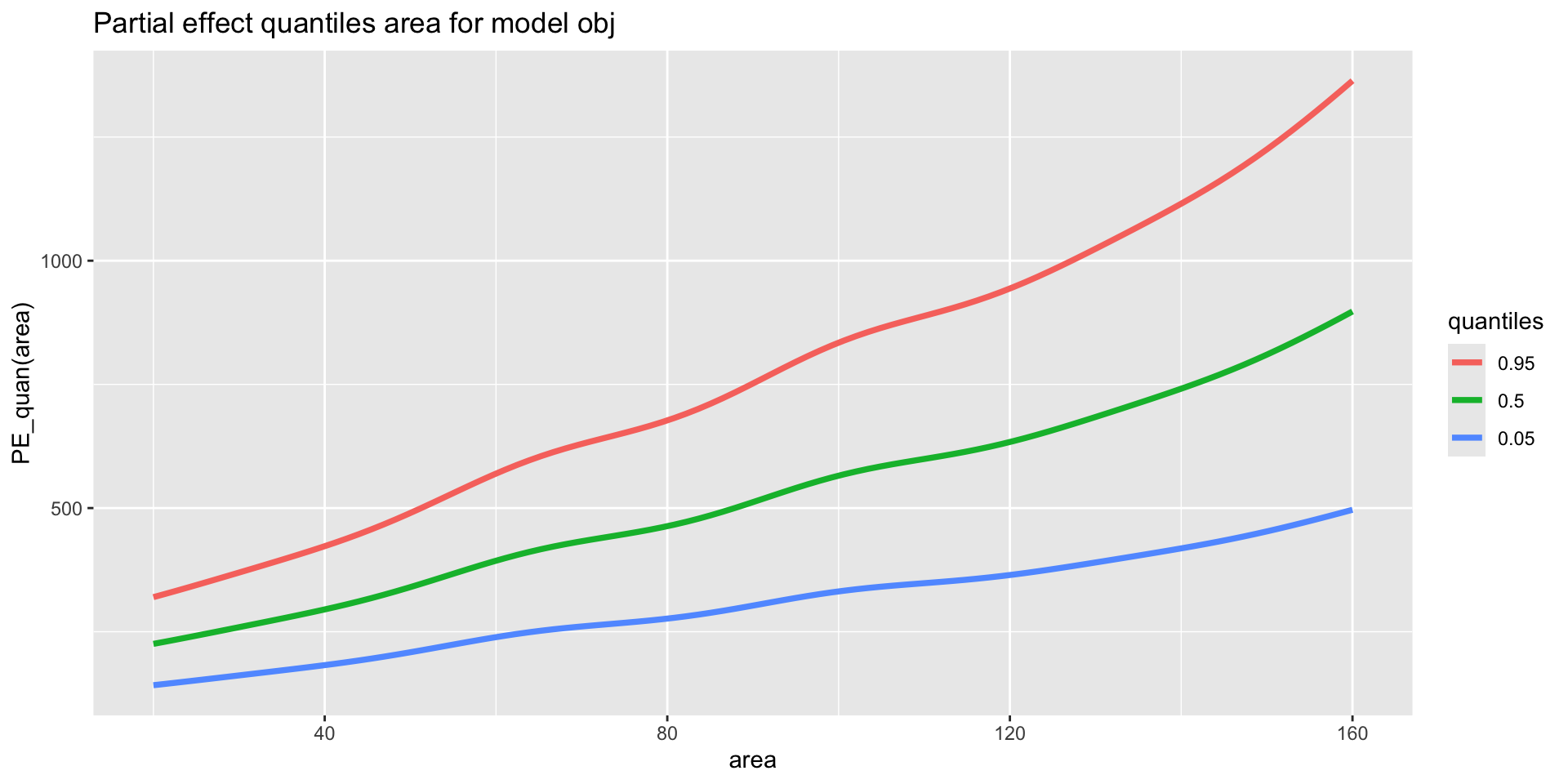
quantiles, additive (con.)
quantiles interactions
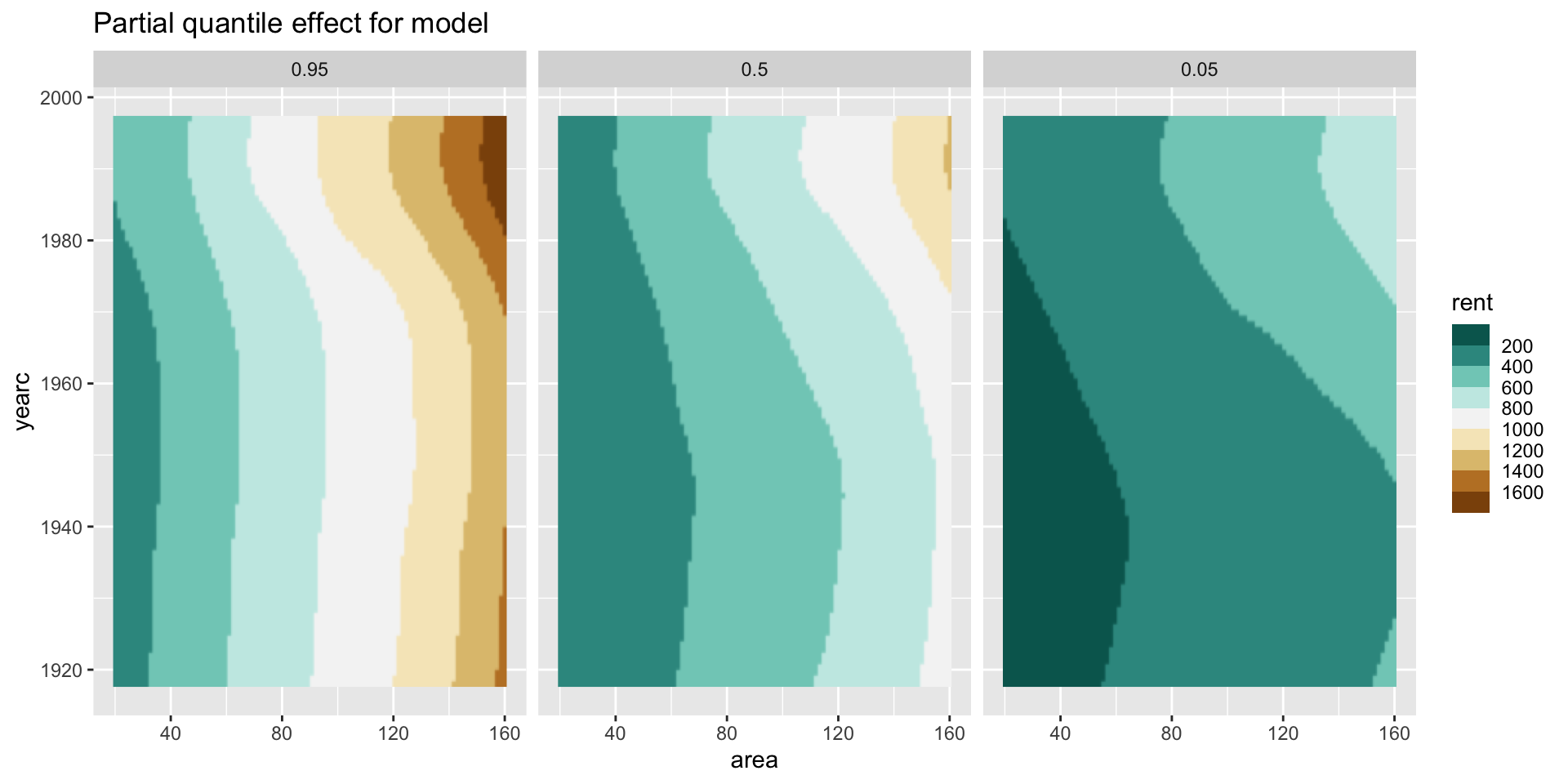
quantiles interactions 2
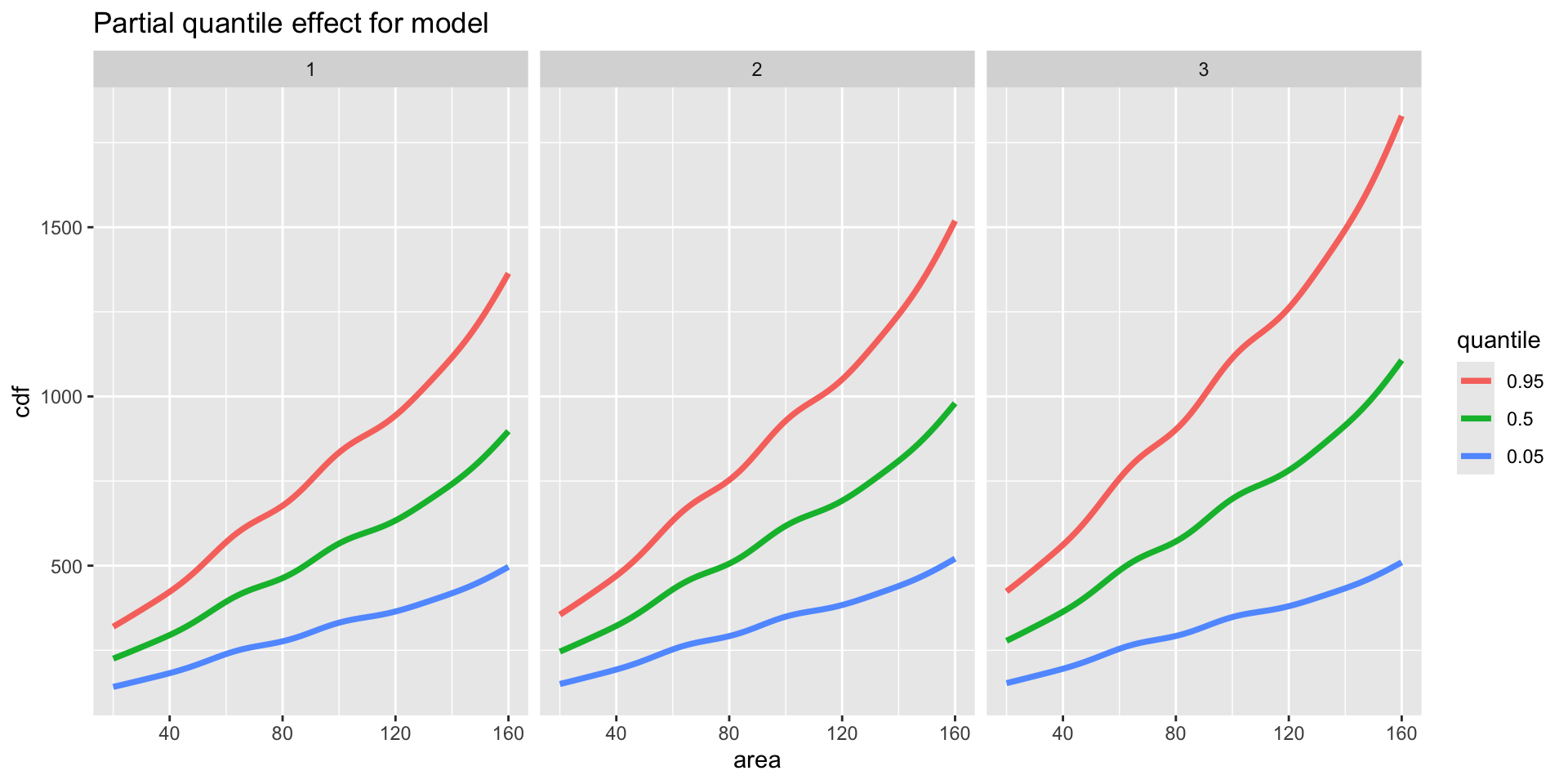
quantiles interactions 2
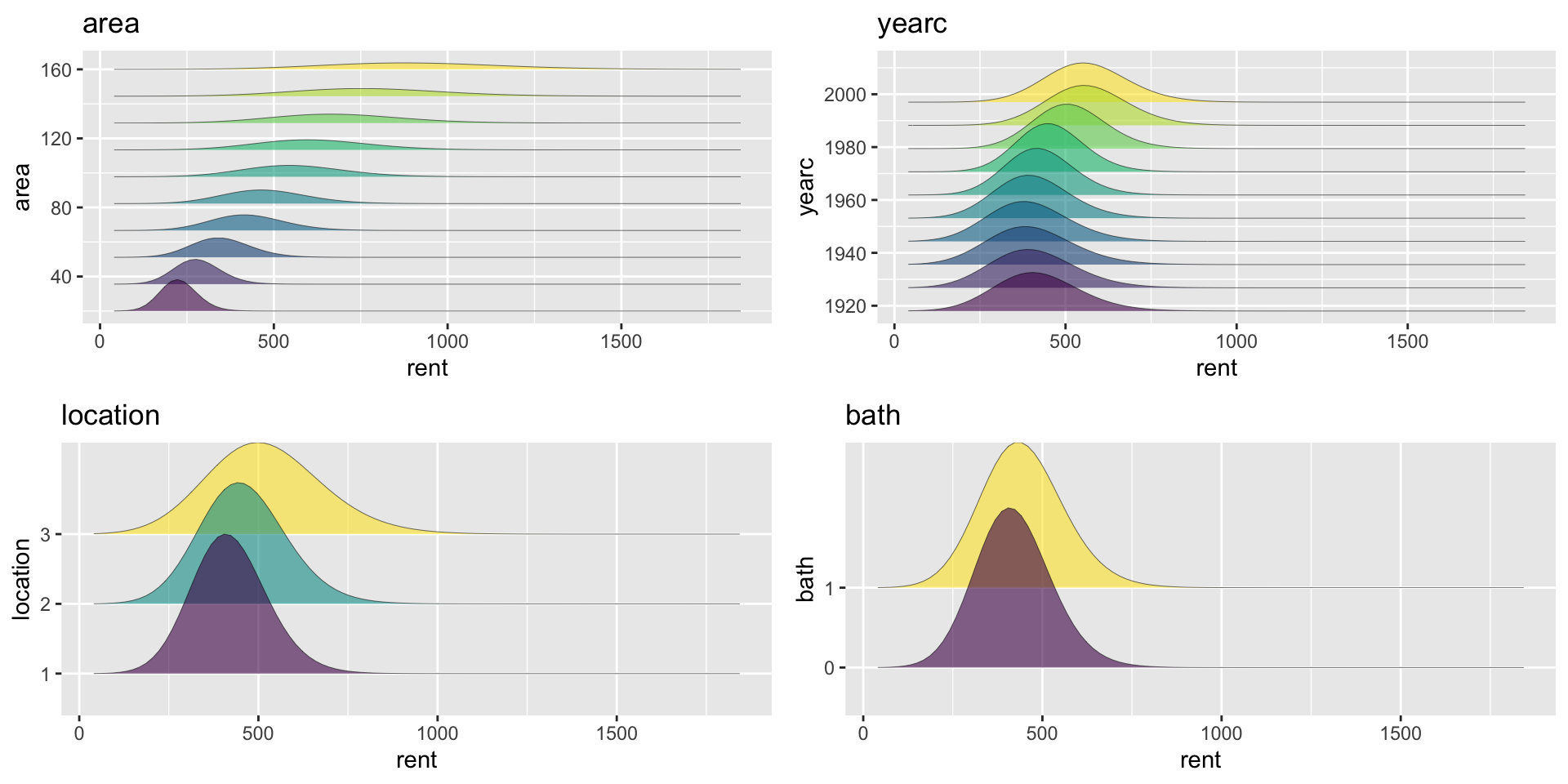
distributions, \(\mu\), additive
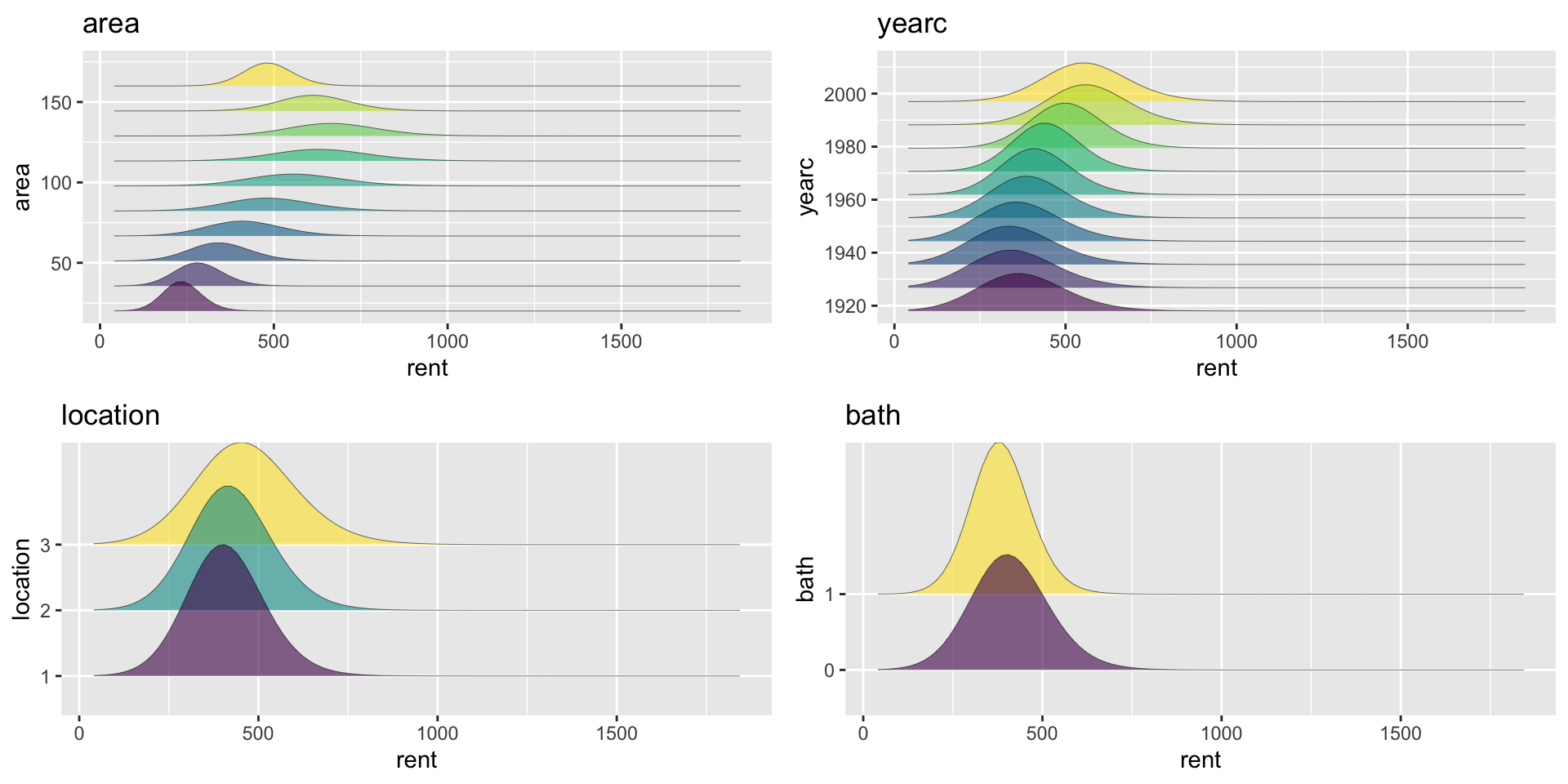
distributions, \(\mu\), NN
the purpose of the study
the
purposeshould be always in our mind when we try to analyse any datafor the Munich rent data are collected almost every 10 years
guidance to judges on whether a disputed rent is a fair or not
purposeis to identify very low or very hight rents by correcting for the explanatory variablessimilar in detecting “outliers”
a possible solution:
prediction z-scores
prediction z-scores
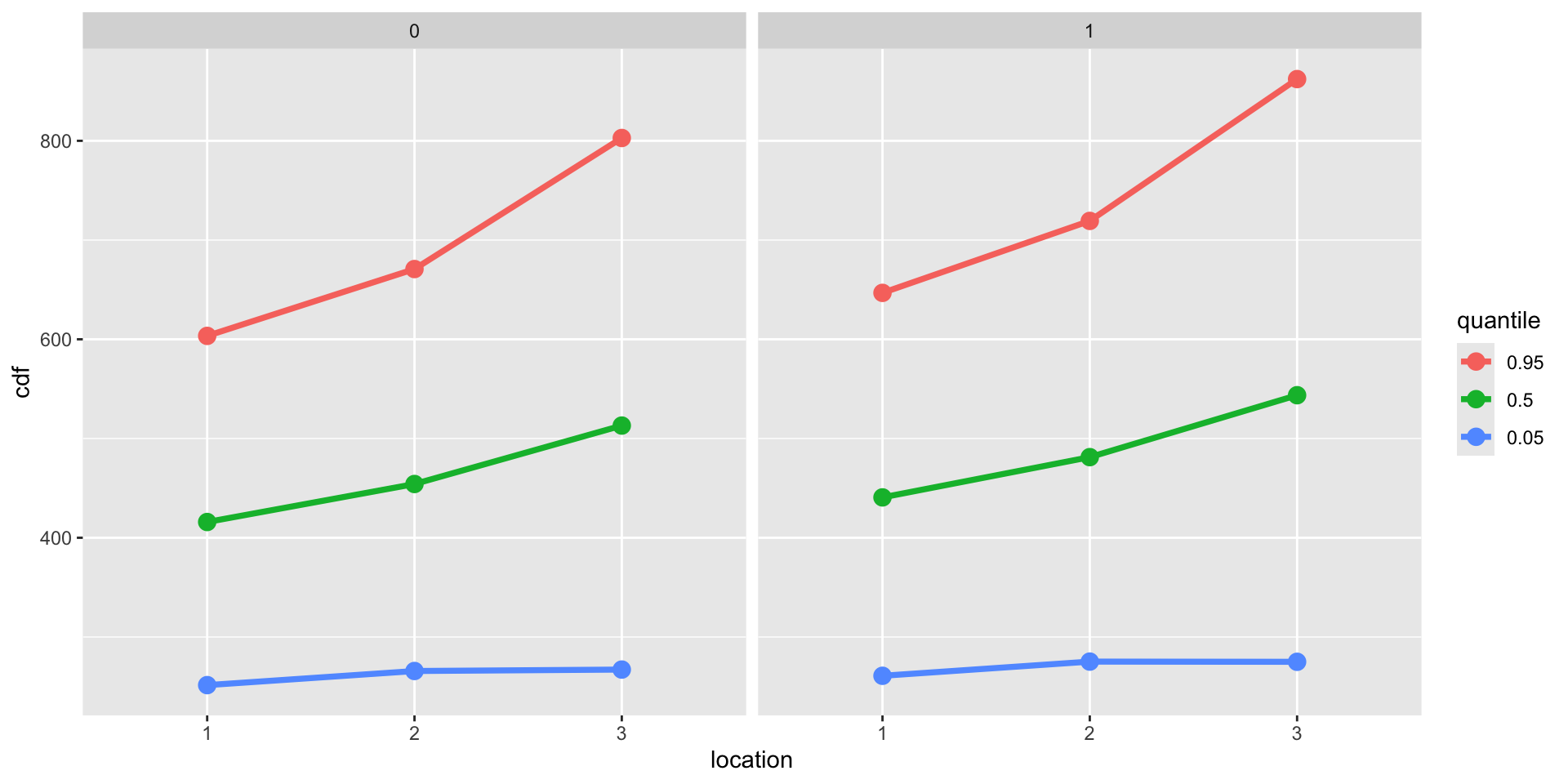
Scenarios
| rent | area | yearc | location | bath | kitchen | heating |
|---|---|---|---|---|---|---|
| 1500 | 140 | 1983 | 3 | 1 | 1 | 1 |
| 1000 | 55 | 1915 | 1 | 0 | 0 | 0 |
| 800 | 65 | 1960 | 1 | 1 | 1 | 1 |
prediction z-scores (con.)
rent <- c(1500, 1000,800)
area <- c(140, 55, 65)
yearc <- c(1983, 1915, 1960)
location <- factor(c(3,1,1))
bath <- factor(c(1,0,1))
kitchen <- factor(c(1,0,1))
cheating <- factor(c(1,0,1))
ndat <- data.frame(rent, area, yearc, location, bath, kitchen, cheating)
cat("prediction z-scores", "\n")prediction z-scores pp <-predict(madditive, newdata=ndat, type="parameter")
qNO(madditive$family$p(q=ndat$rent, par=pp))[1] 0.2589106 4.7675783 2.1005927summary
GAMLSS can tackle problems where the interest of the investigation lies not only in the center but other parts of the distribution.
Personal view for the future of GAMLSS development;
theoretical contributions
software and
knowledge exchange
Summary (continue)
theoretical contributions- interpretable tools
- model average for prediction
softwaregamlss2
books and knowledge exchange- there is need for applied and elementary books
- more application public health and environment
the team
| working party | current | past |
|---|---|---|
Gillian Heller |
Konstantinos Pateras |
Popi Akantziliotou |
Fernanda De Bastiani |
Paul Eilers | Vlasios Voudouris |
Thomas Kneib |
Nikos Kametas | Nicoleta Mortan |
Achim Zaileis |
Tim Cole |
Daniil Kiose |
Andreas Mayr |
Nikos Georgikopoulos |
Dea-Jin Lee |
Nicolaus Umlauf |
Luiz Nakamura |
María Xosé Rodríguez-Álvarez |
Reto Stauffer |
Nadja Klein | Majid Djennad |
Robert Rigby |
Julian Merder |
Fiona McElduff |
Mikis Stasinopoulos |
Abu Hossain | Raydonal Ospina |
discussion
end


 The Books
The Books

www.gamlss.com