Distributions

Mikis Stasinopoulos
Bob Rigby
Gillian Heller
Fernanda De Bastiani
Niki Umlauf

Introduction

Suitable distribution for the response variable.

  • different types of distributions

  • properies of distributions

  • distributions in GAMLSS

    • explicit
    • implicit

  • a procedure to find a good initial distribution for the response

distributions

Types

  • continuous

    • \((-\infty, \infty)\), real line;
    • \((0, \infty)\), positive real line;
    • \((0,1)\) from 0 to 1

  • discrete

    • \((0,1,\dots, \infty)\)
    • \((0,1,\dots, N)\)

  • mixed part continuous part discrete

    • \([0, \infty)\) zero adjusted
    • \([0, 1]\) zero (and 1) inflated

continuous

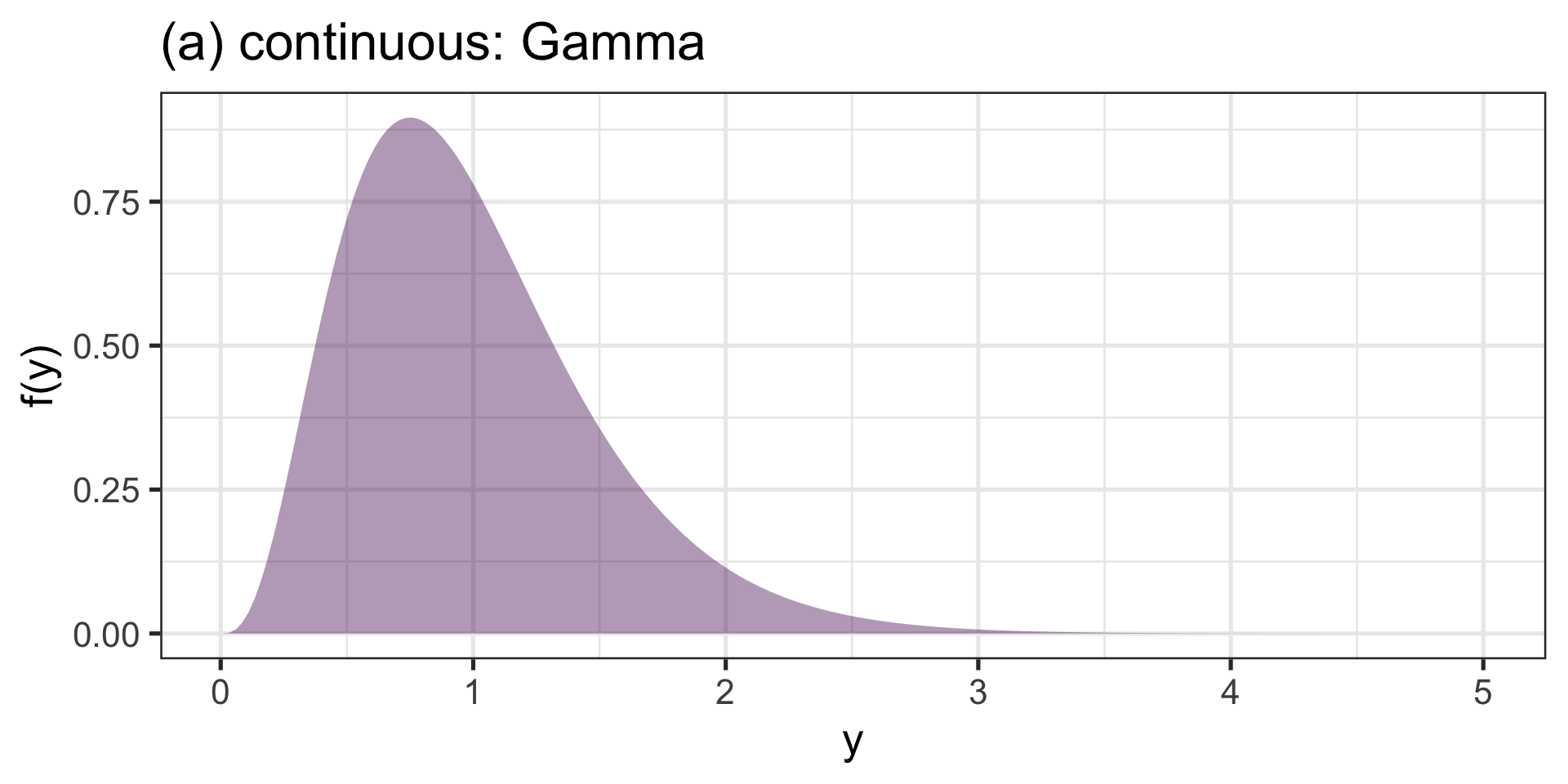
(a) continuous

discrete

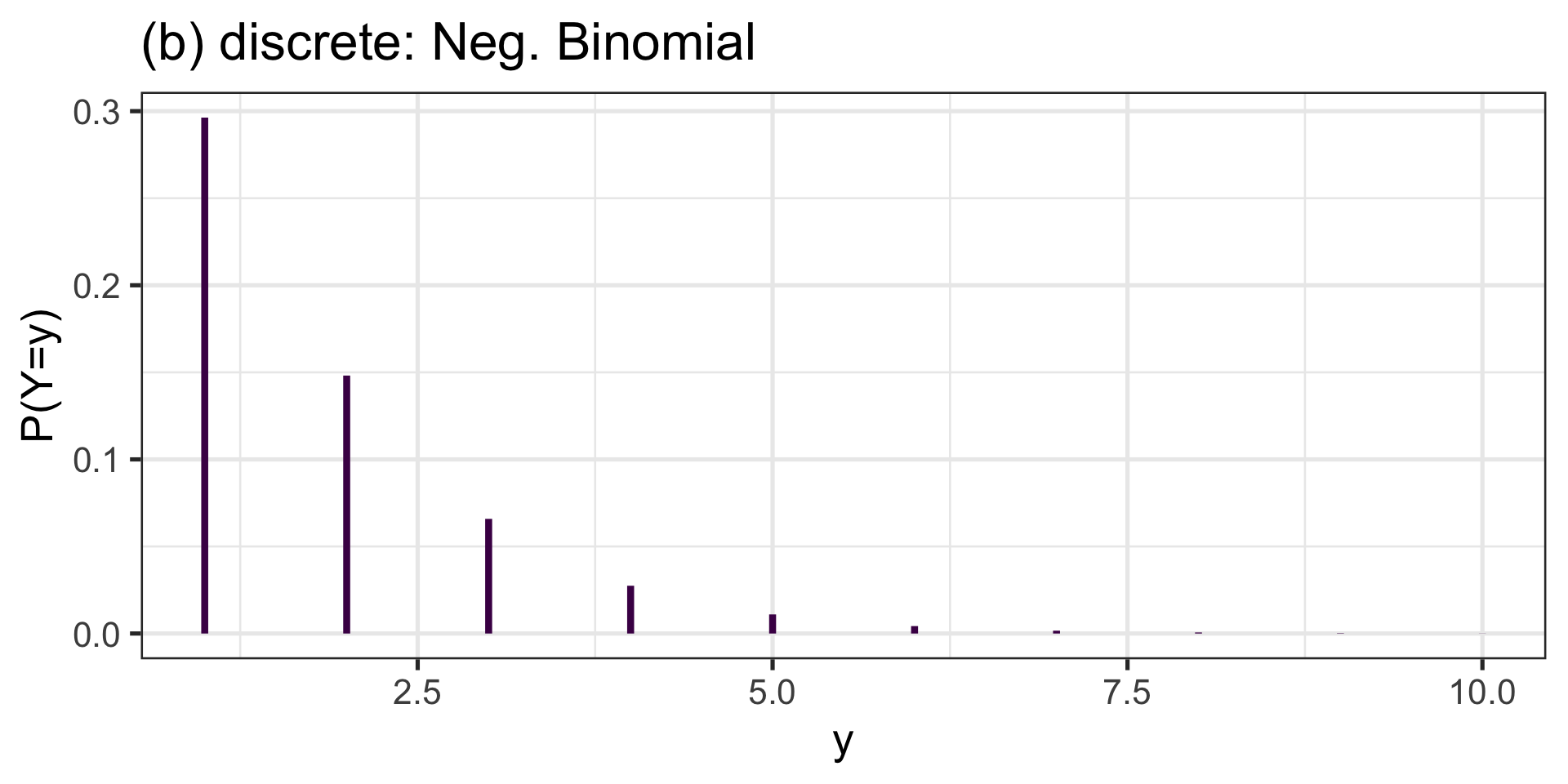
(a) discrete

mixed

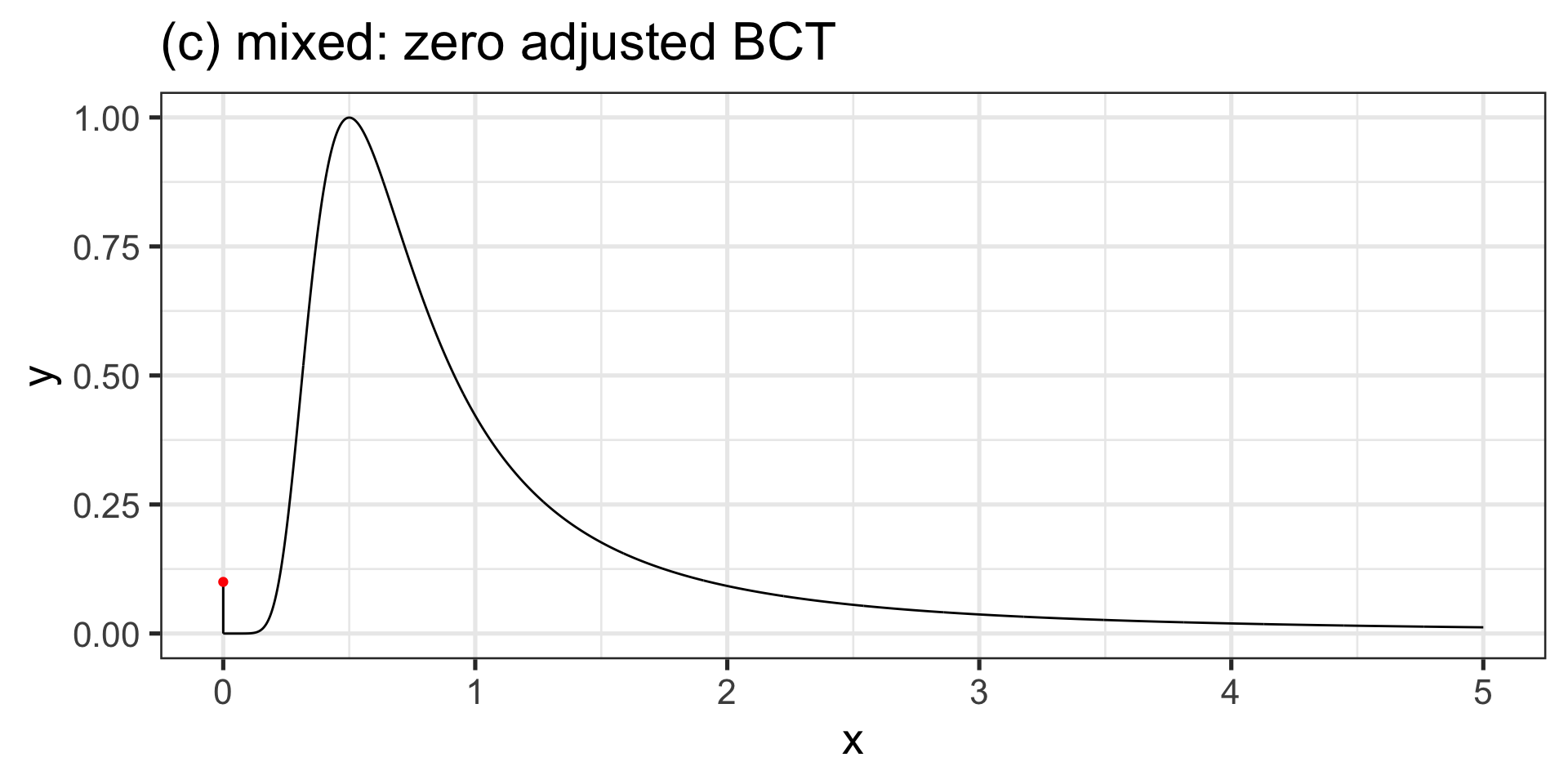
(a) mixed

properties

\(f(y;{\theta})\)

  • \(\int_{R_Y} f(y) \; dy=1\)

  • \(\sum_{y\in R_Y} f(y)=\sum_{y \in R_Y} P(Y=y)=1\)

  • \(\int_{R_{1}} f(y)\, dy + \sum_{y \in R_{2}} f(y) = 1\).

parameters

  • \(f(y;{\theta})\)

  • \({\theta}= (\theta_1, \theta_2, \ldots, \theta_k)\).

  • location

  • scale

  • shape

    • skewness
    • kurtosis

left skew

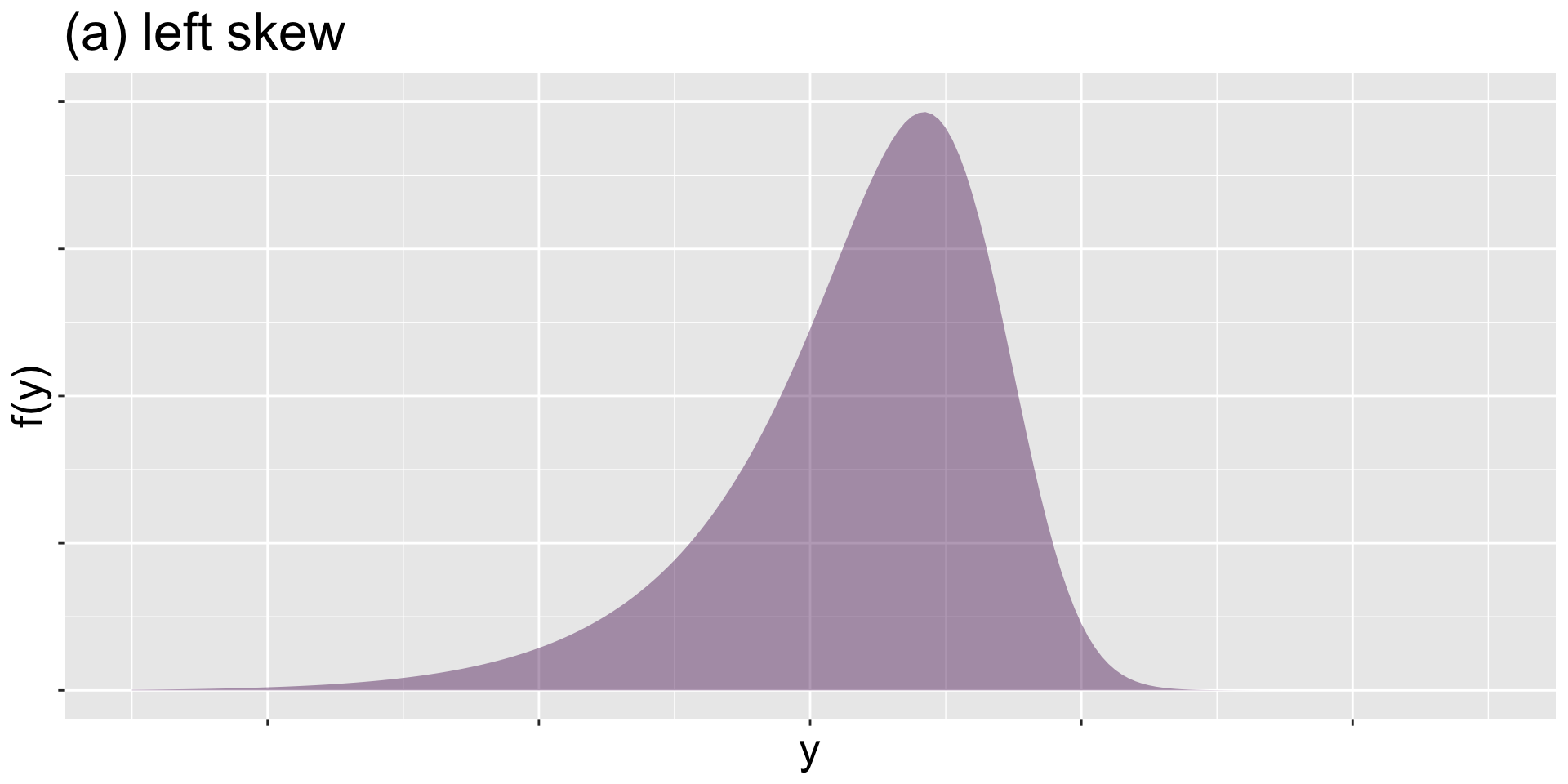
(a) left skew

symmetric

(a) symmetric

right skew

Figure 6: right skew

platy

(a) platy

meso

Figure 8: meso

lepto

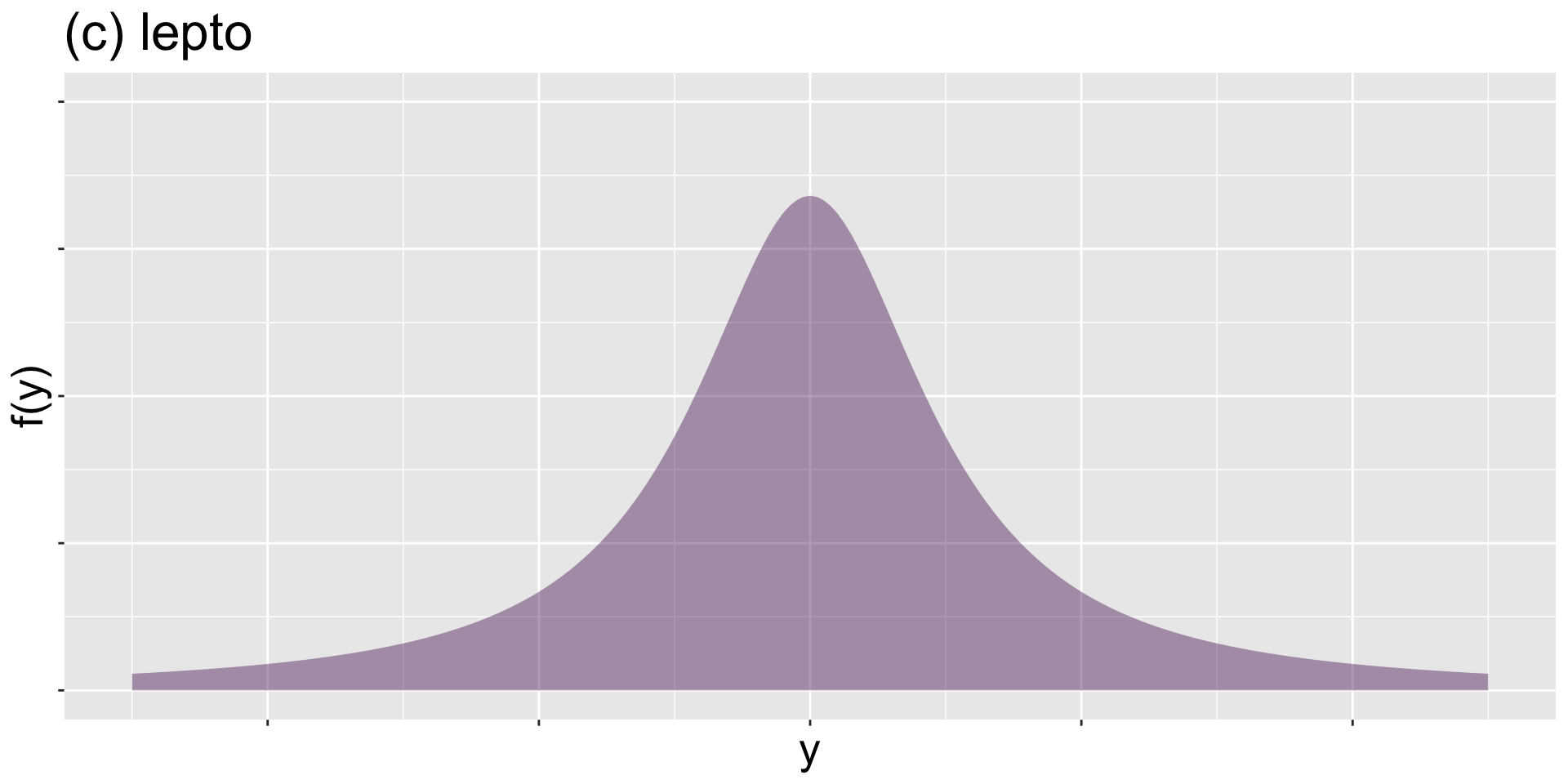
Figure 9: lepto

moments based characteristics

  • mean \[\begin{align*} E(Y)= \begin{cases} \int_{-\infty}^{\infty} y f(y)\, dy&\text{for continuous}\\ \sum_{y \epsilon R_Y} y\, P(Y=y) &\text{for discrete} \end{cases} \end{align*}\]

  • variance

  • coefficient of skewness

  • (adjusted) coefficient for kurtosis

mean

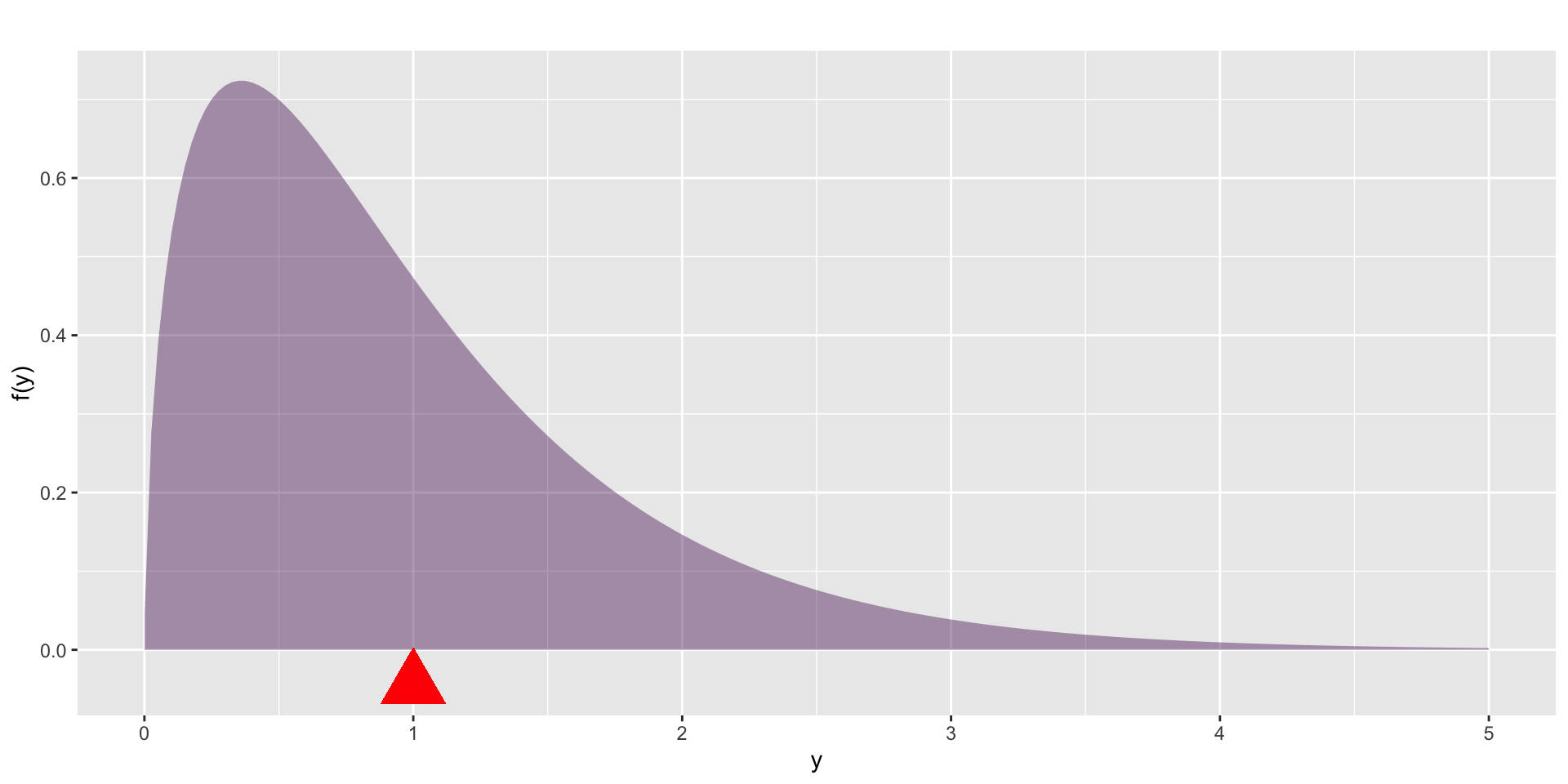
Figure 10: The mean is the point in which the distribution is balance.

centile based characteristics

  • the median

  • semi interquartile range

  • centile skewness

  • centile kurtosis

quantiles

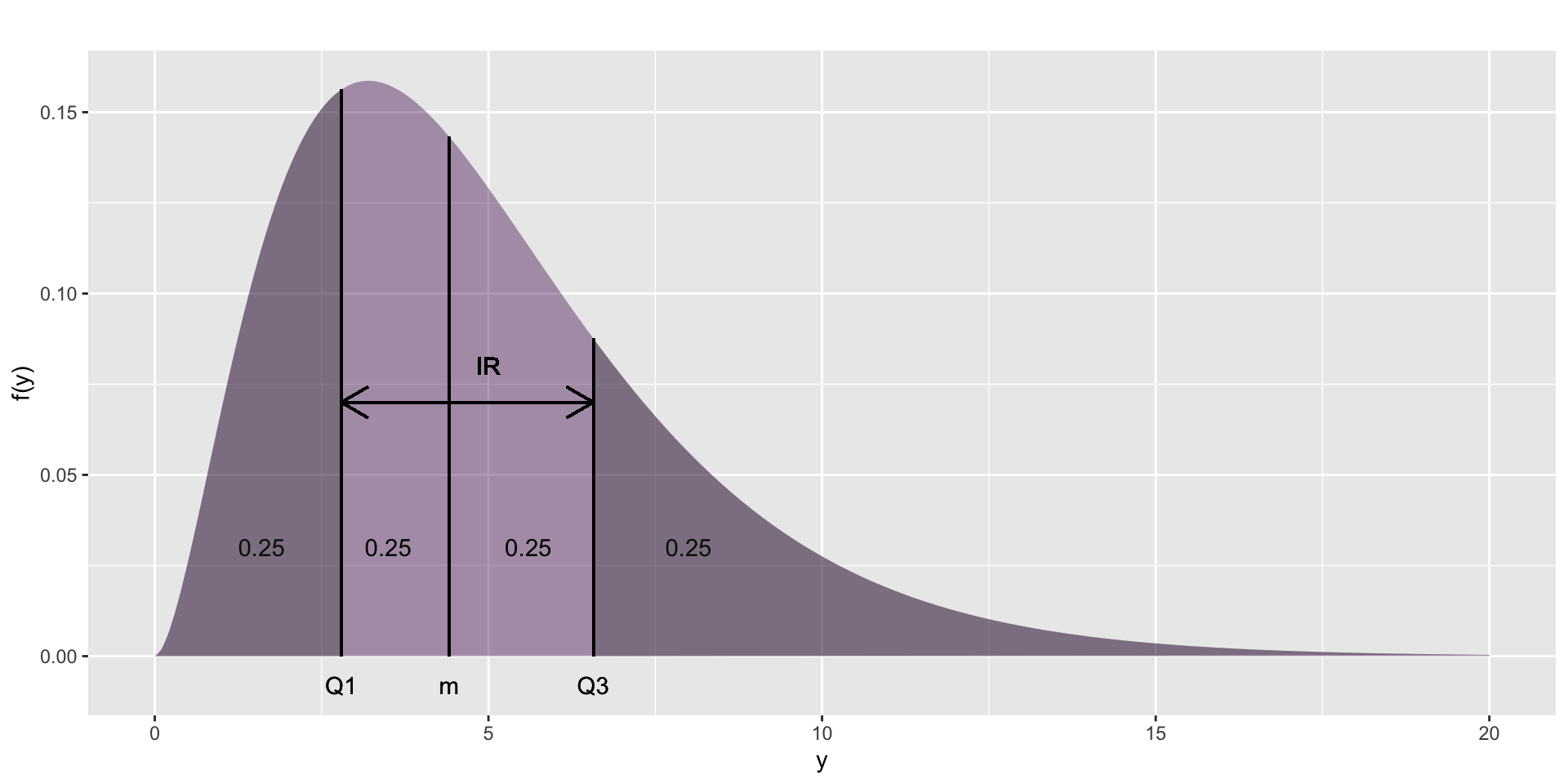
Figure 11: Showing how \(Q1\), \(m\) (median), \(Q3\) and the interquartile range IR of a continuous distribution are derived from \(f(y)\).

The GAMLSS families

  • over 100 explicit distributions

  • implicit distributions

    • truncation
    • log distributions
    • logit distribution
    • inflated distributions
    • zero adjusted
    • generalised Tobit

explicit distributions

  • d probability density functions (pdf)

  • p cumulative density functions (cdf)

  • q the q-function or inversed cumulative density functions (icdf)

  • r random generating function

  • fitting function

    • first and second devivative of the log-likelihood
    • other information like names of parameters, range of the response a of the parameters e.t.c.

continuous

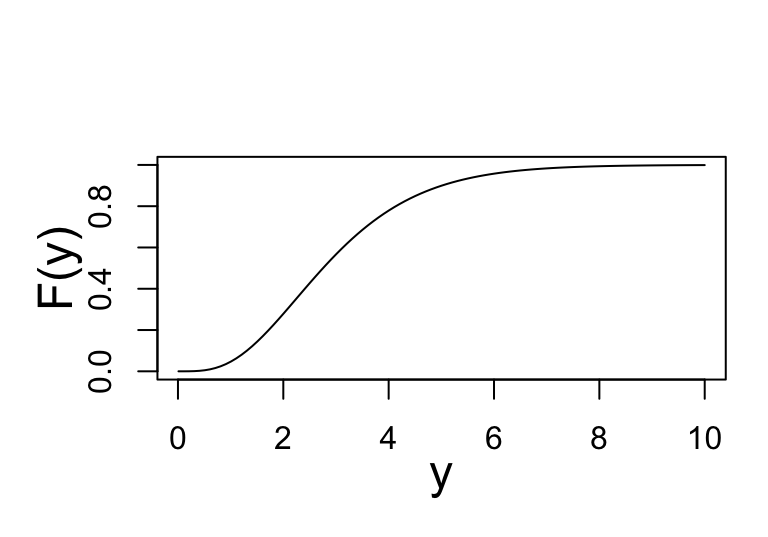
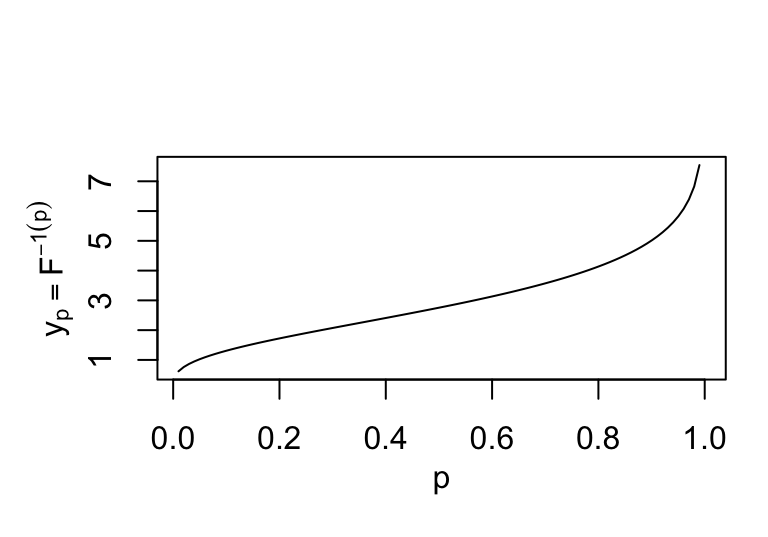
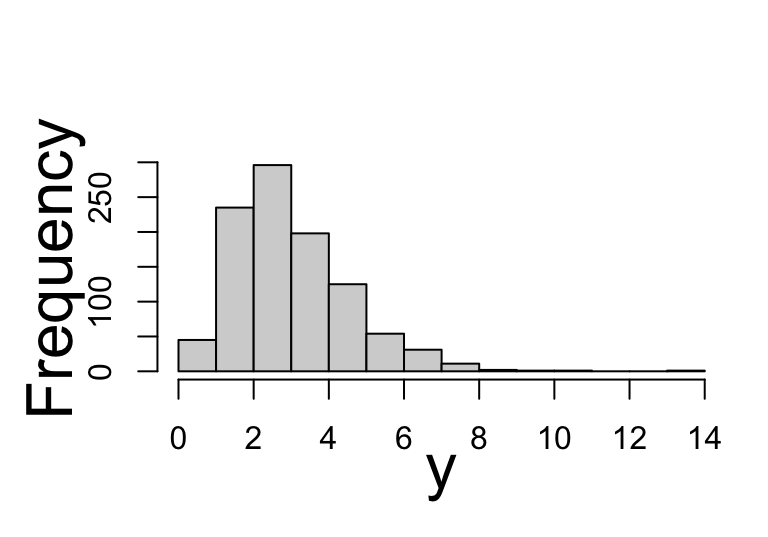
with ggplot2

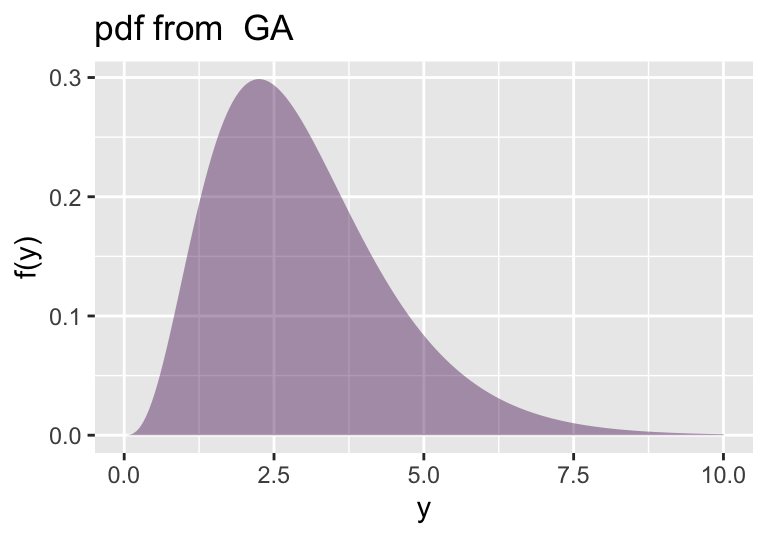
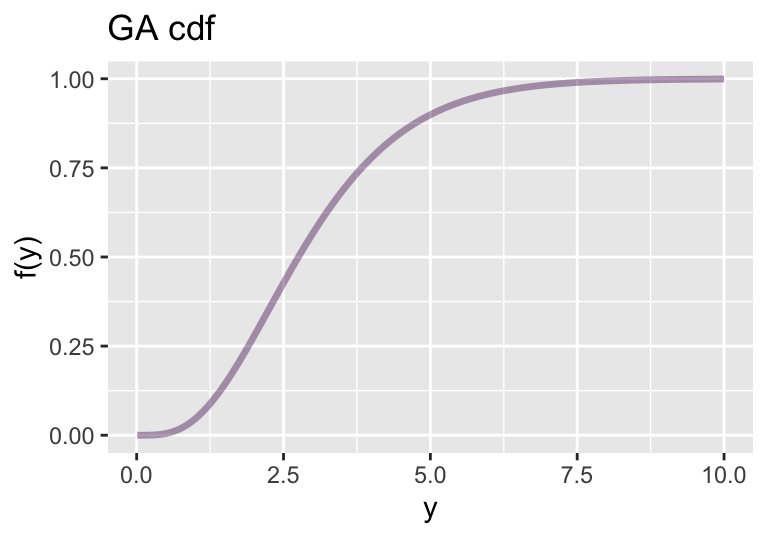
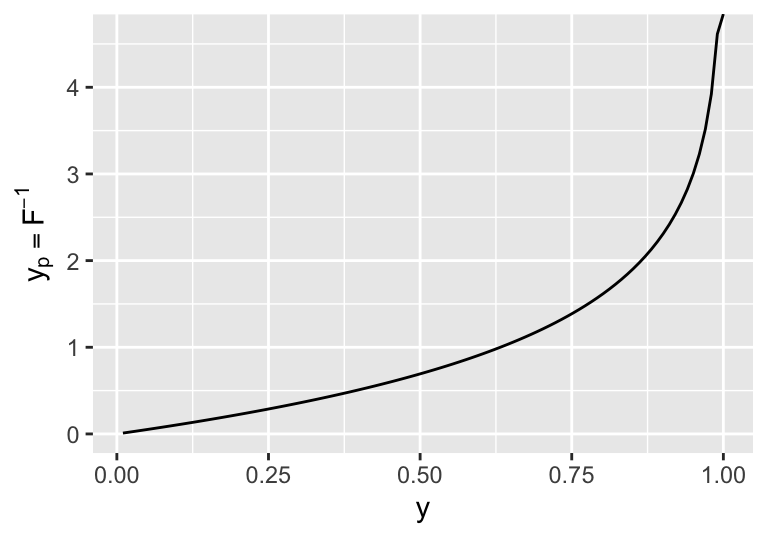
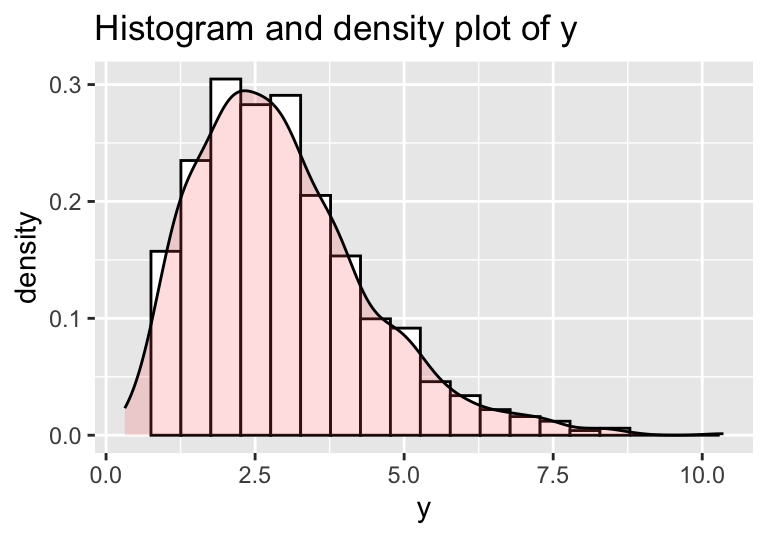
discrete

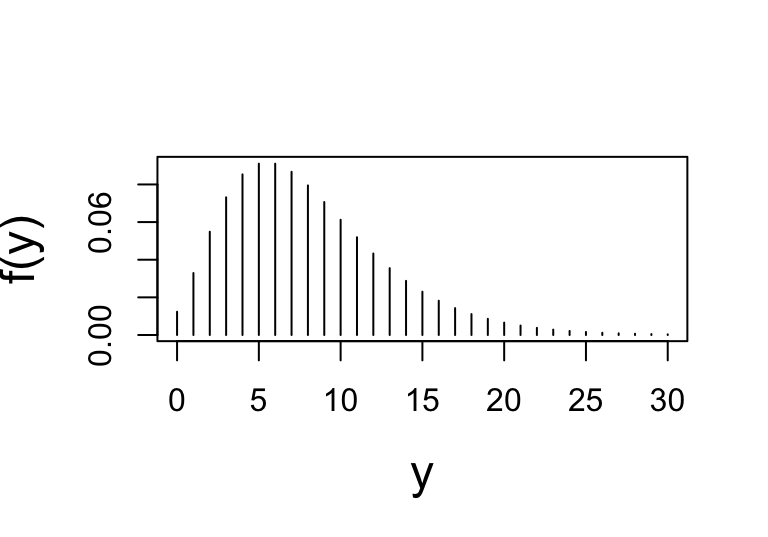
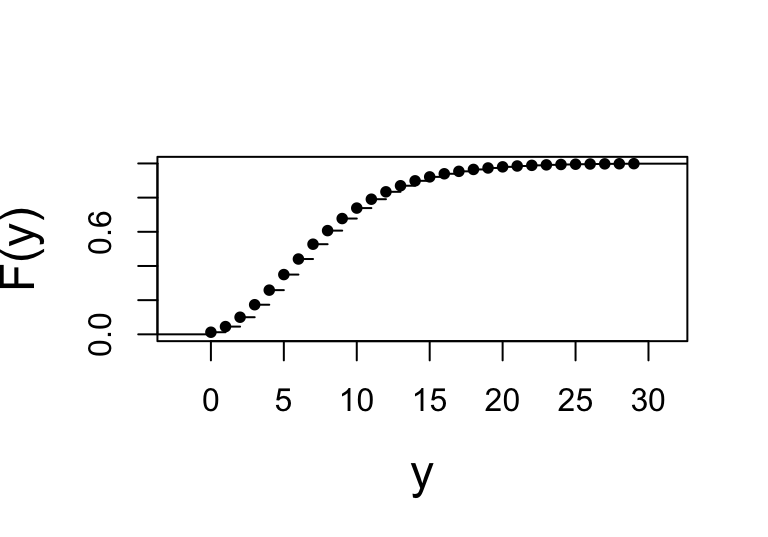
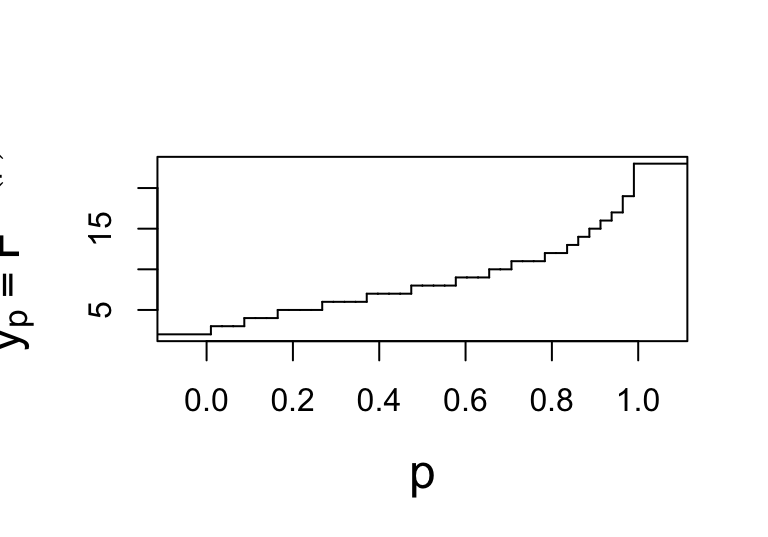
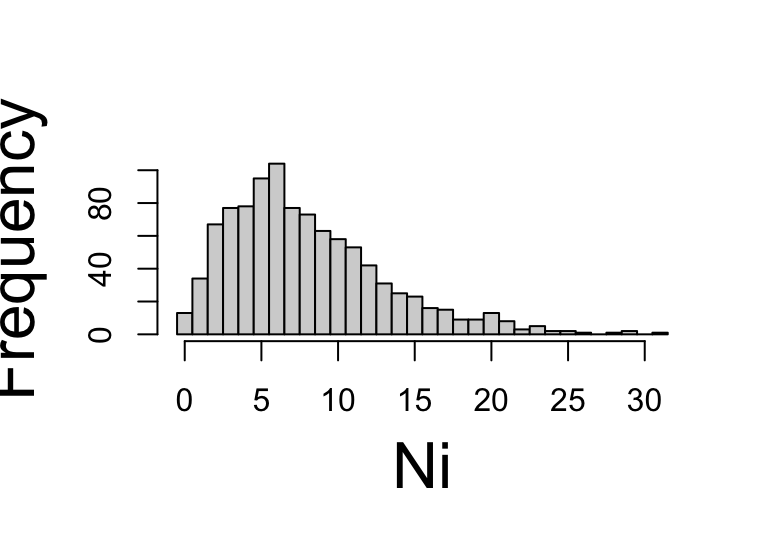
with ggplot2

demo

library(gamlss.demo)
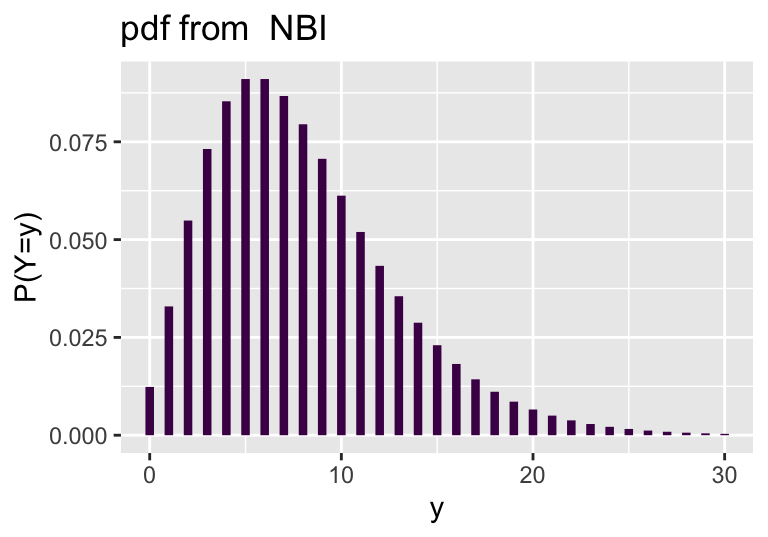
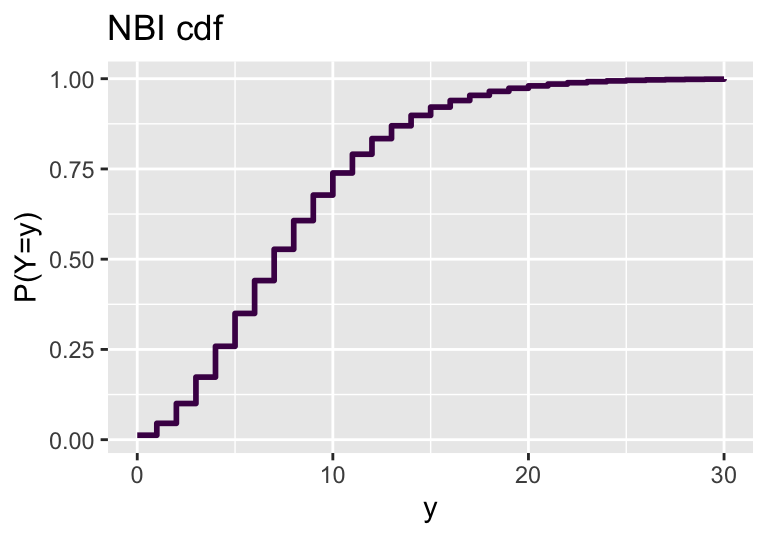
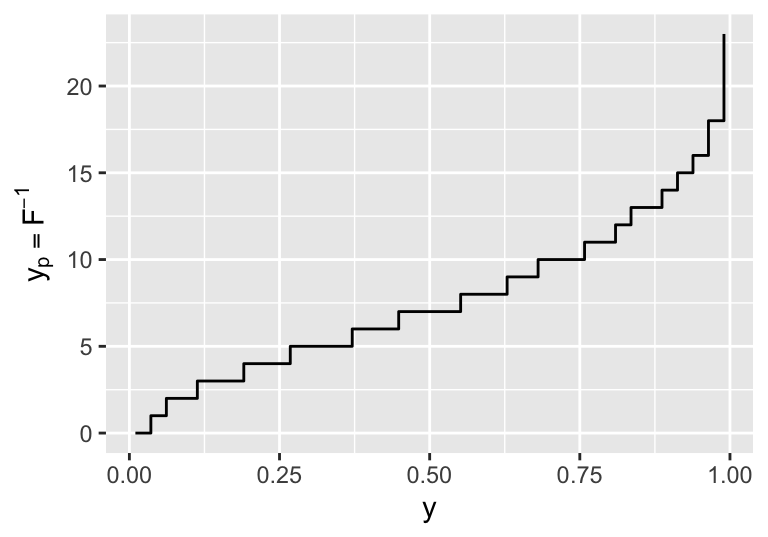
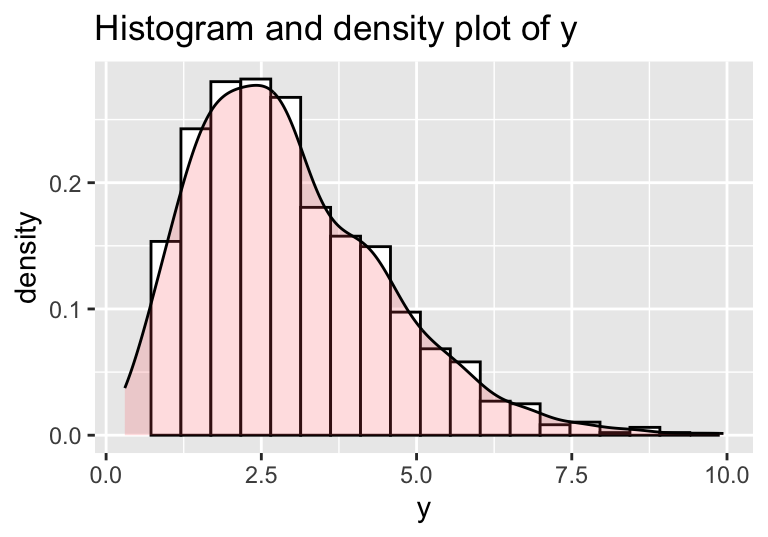
gamlss.demo()

implicit distributions

truncated distributions

  • Any distribution can be truncated

    – to the left

    – to the right or

    – in both sides

truncated continuous

library(gamlss.tr)
gen.trun("NO", par=c(0,3), type="both")
A truncated family of distributions from NO has been generated 
 and saved under the names:  
 dNOtr pNOtr qNOtr rNOtr NOtr 
The type of truncation is both 
 and the truncation parameter is 0 3  
family_pdf("NOtr", from=0,to=3, mu=0, sigma=1)
integrate(dNOtr, 0,3)
1 with absolute error < 1.1e-14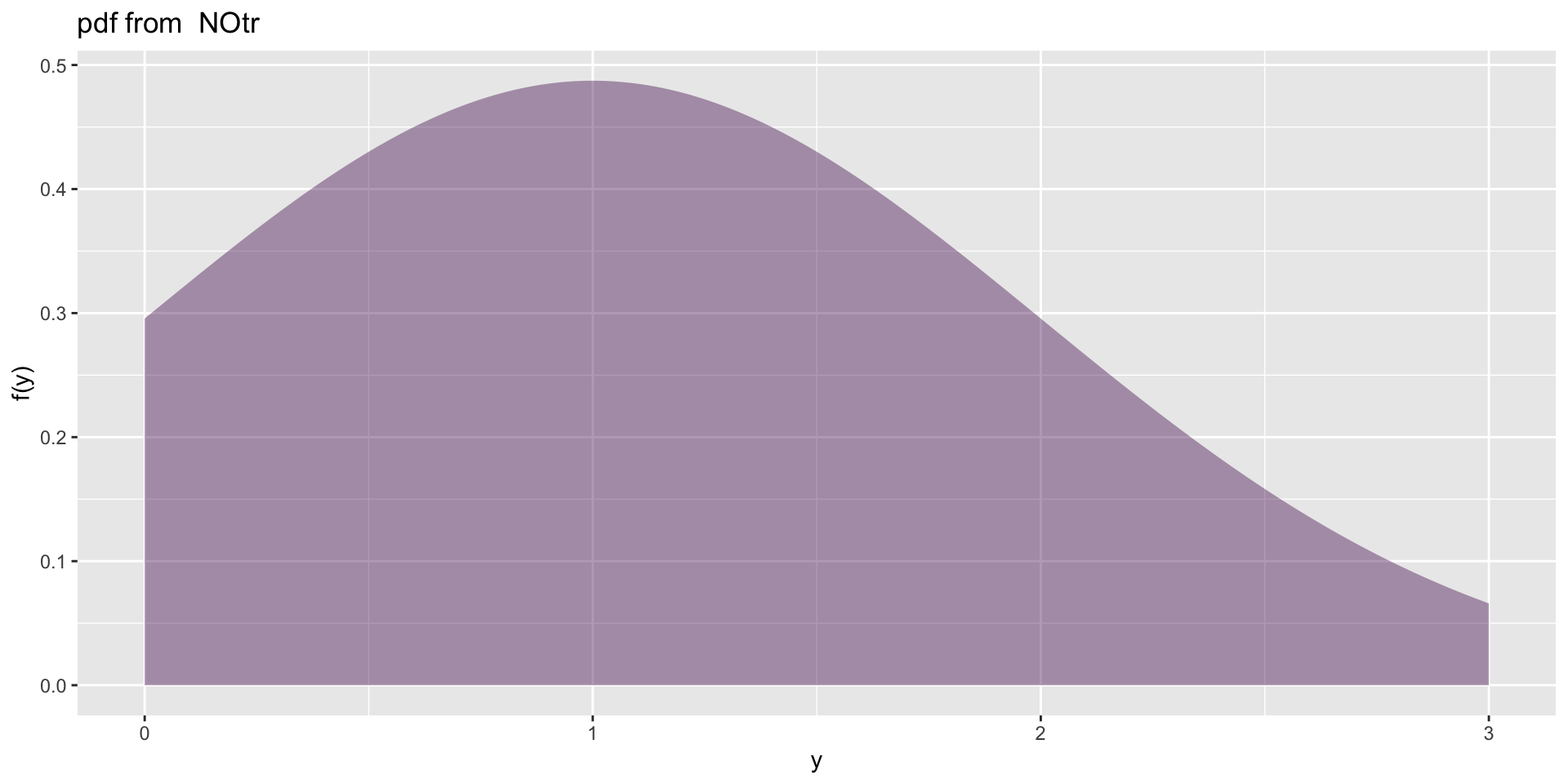

truncated discrete

gen.trun("NBI", par=0)
A truncated family of distributions from NBI has been generated 
 and saved under the names:  
 dNBItr pNBItr qNBItr rNBItr NBItr 
The type of truncation is left 
 and the truncation parameter is 0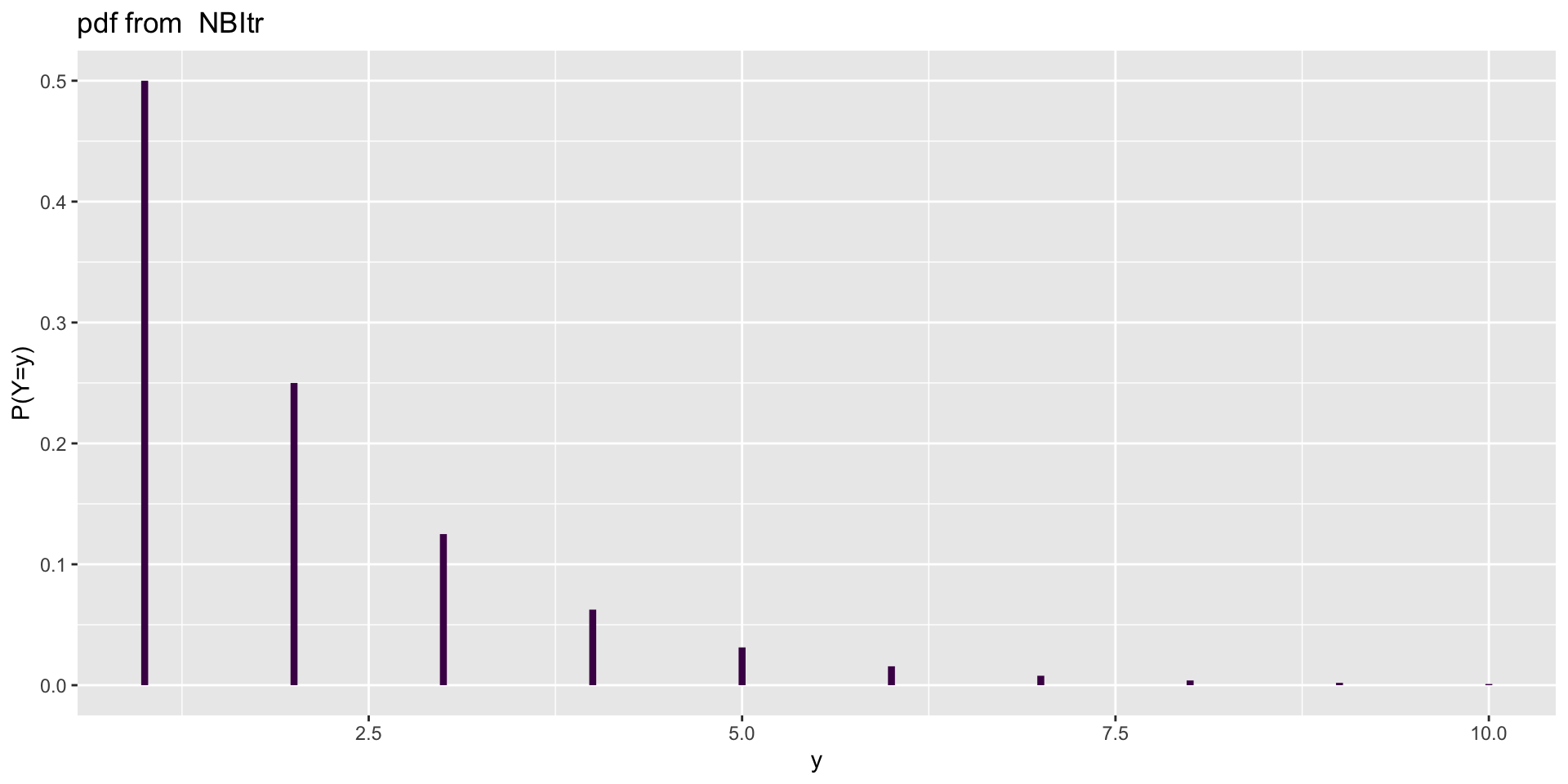  
family_pdf("NBItr", from= 1, to=10, mu=1.5, sigma=1)

Transformation from \((-\infty, \infty)\) to \((0, +\infty)\)

  • Any distribution for \(Z\) on \((-\infty, \infty)\) can be transformed to a corresponding distribution for \(Y=\exp(Z)\) on \((0, +\infty)\)

  • For example: from t distribution to \(\log t\) distribution

log distributions

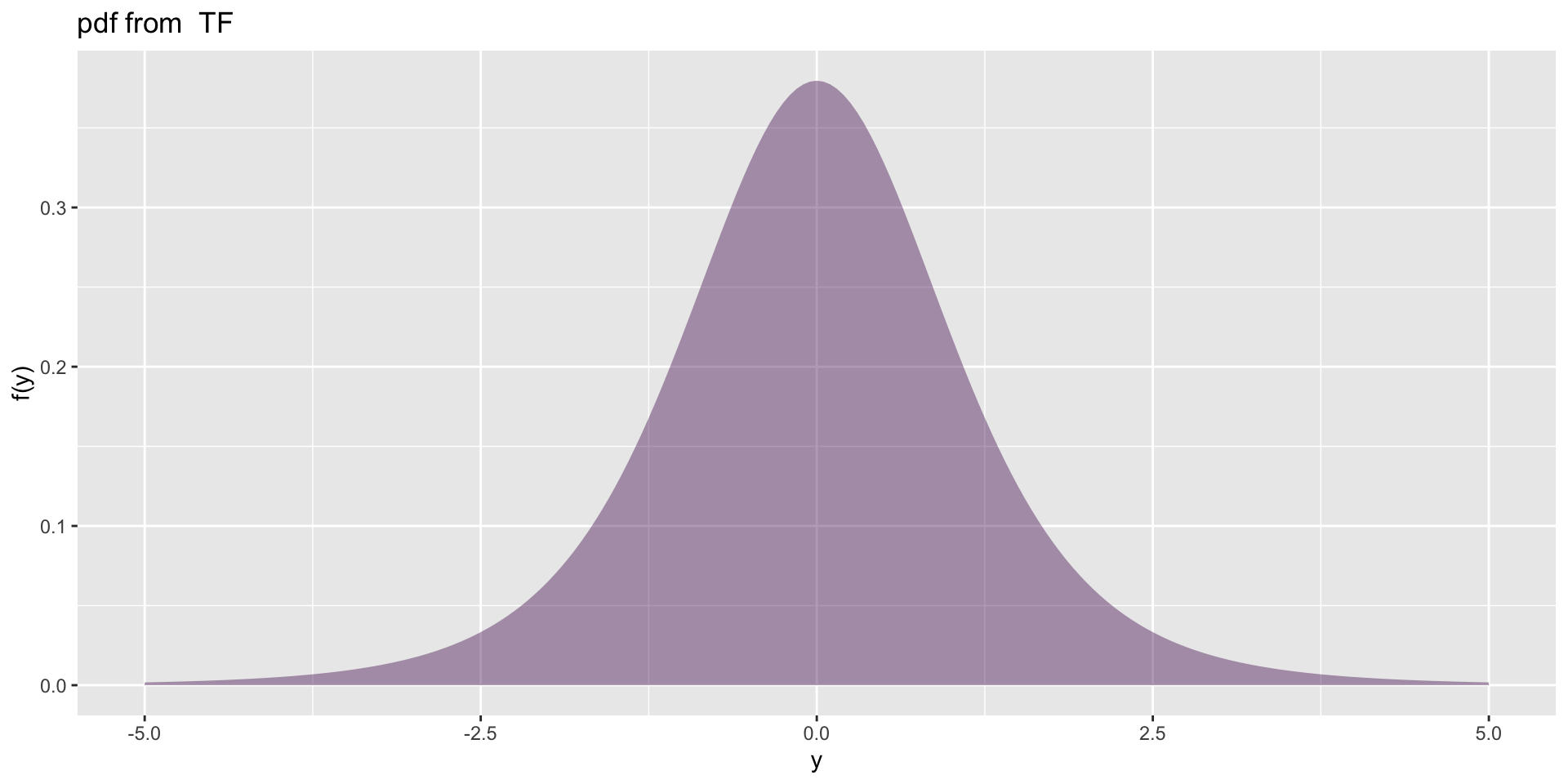
family_pdf("TF", from=-5,to=5, mu=0, sigma=1, nu=5)

log distributions (con)

gen.Family("TF")
A  log  family of distributions from TF has been generated 
 and saved under the names:  
 dlogTF plogTF qlogTF rlogTF logTF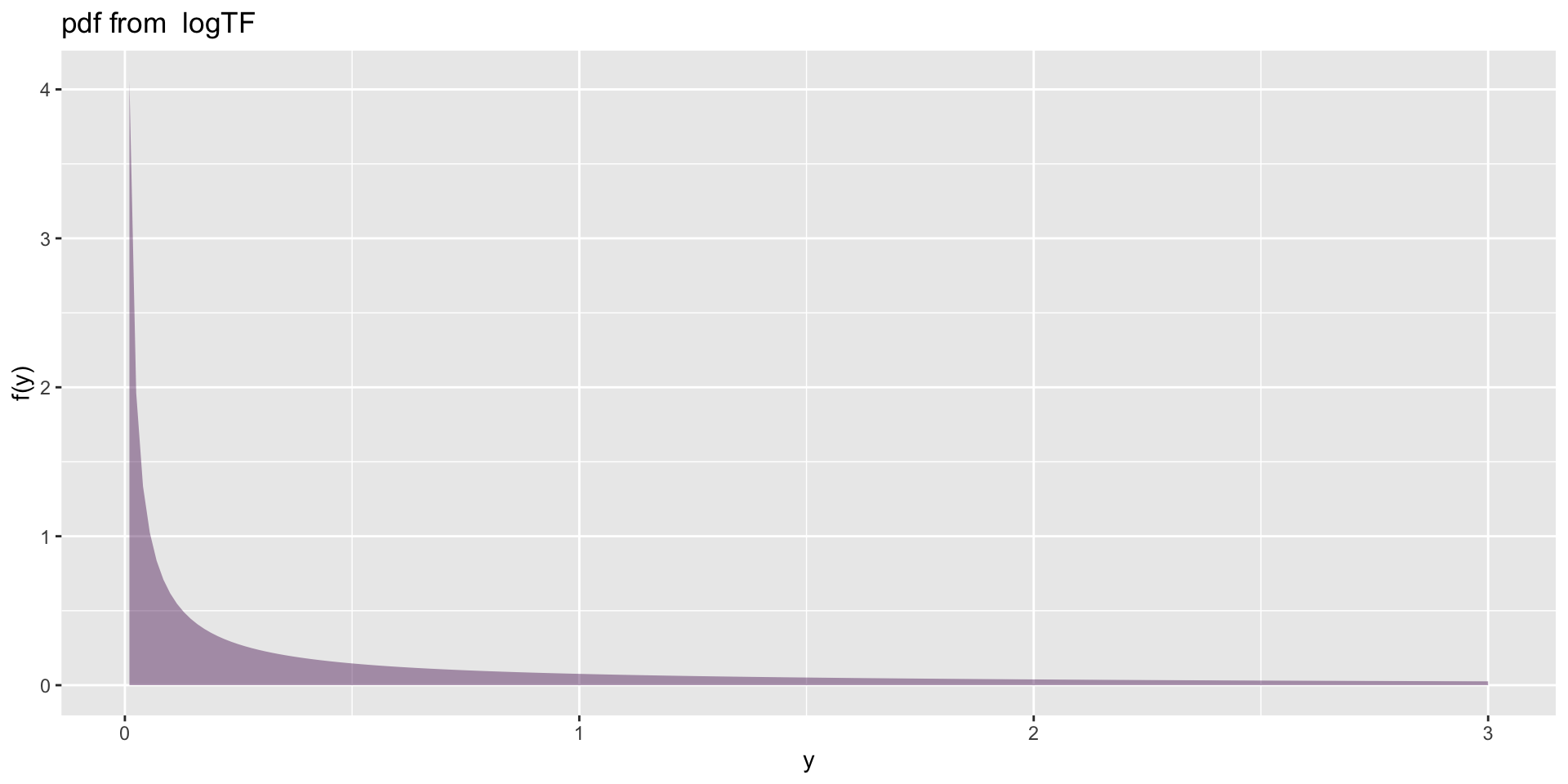 
family_pdf("logTF", from=0.01,to=3, mu=0, sigma=1, nu=5)

Transformation from \((-\infty, \infty)\) to \((0, 1)\)

  • Any distribution for \(Z\) on \((-\infty, \infty)\) can be transformed to a corresponding distribution for \(Y=\exp(Z)\) on \((0, 1)\)

  • For example: from t distribution to logit t distribution

logit distributions

library(gamlss)
library(gamlss.ggplots)
family_pdf("TF", from=-5,to=5, mu=0, sigma=1, nu=5)

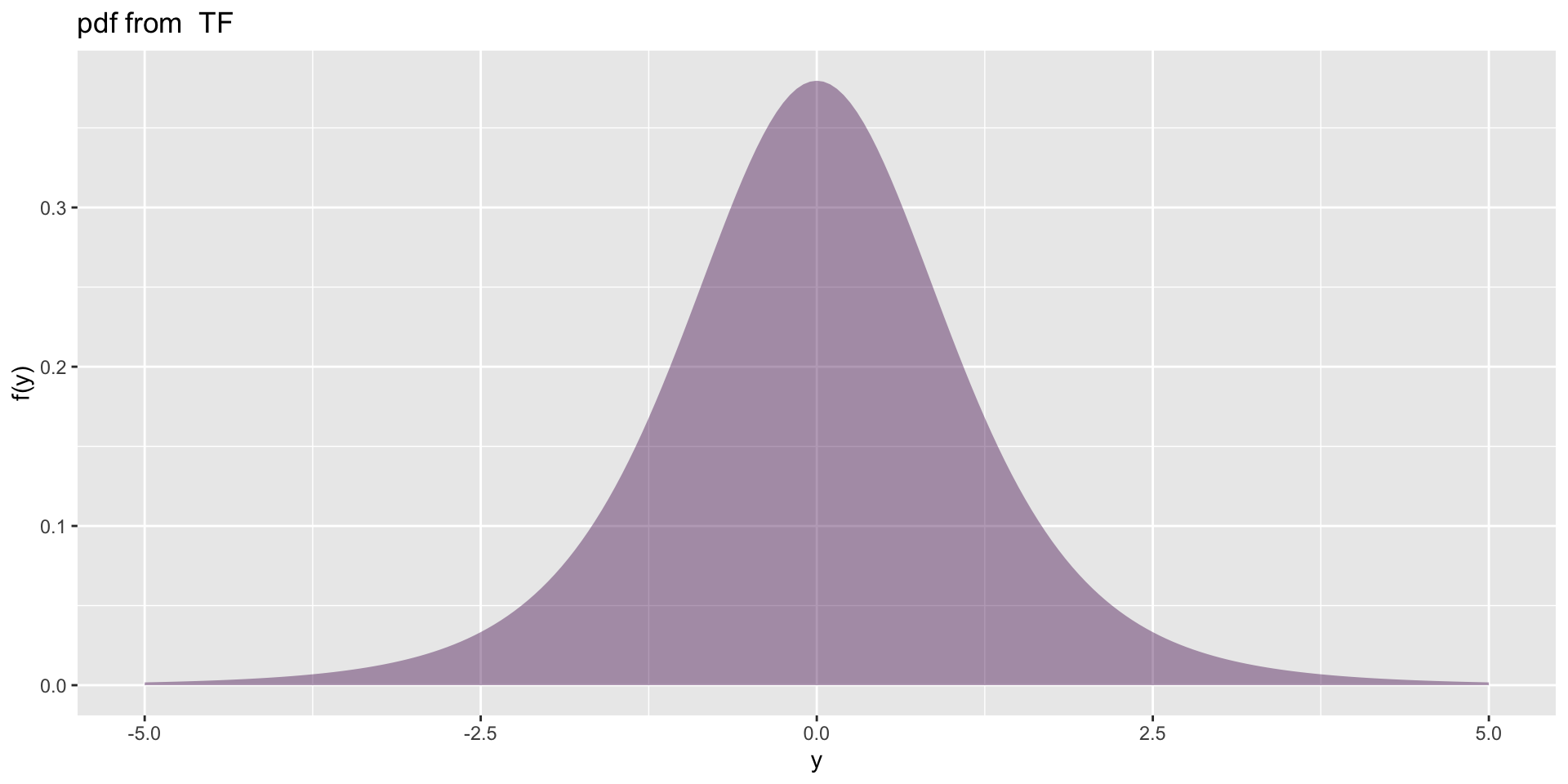
logit distributions (con)

gen.Family("TF", "logit")
A  logit  family of distributions from TF has been generated 
 and saved under the names:  
 dlogitTF plogitTF qlogitTF rlogitTF logitTF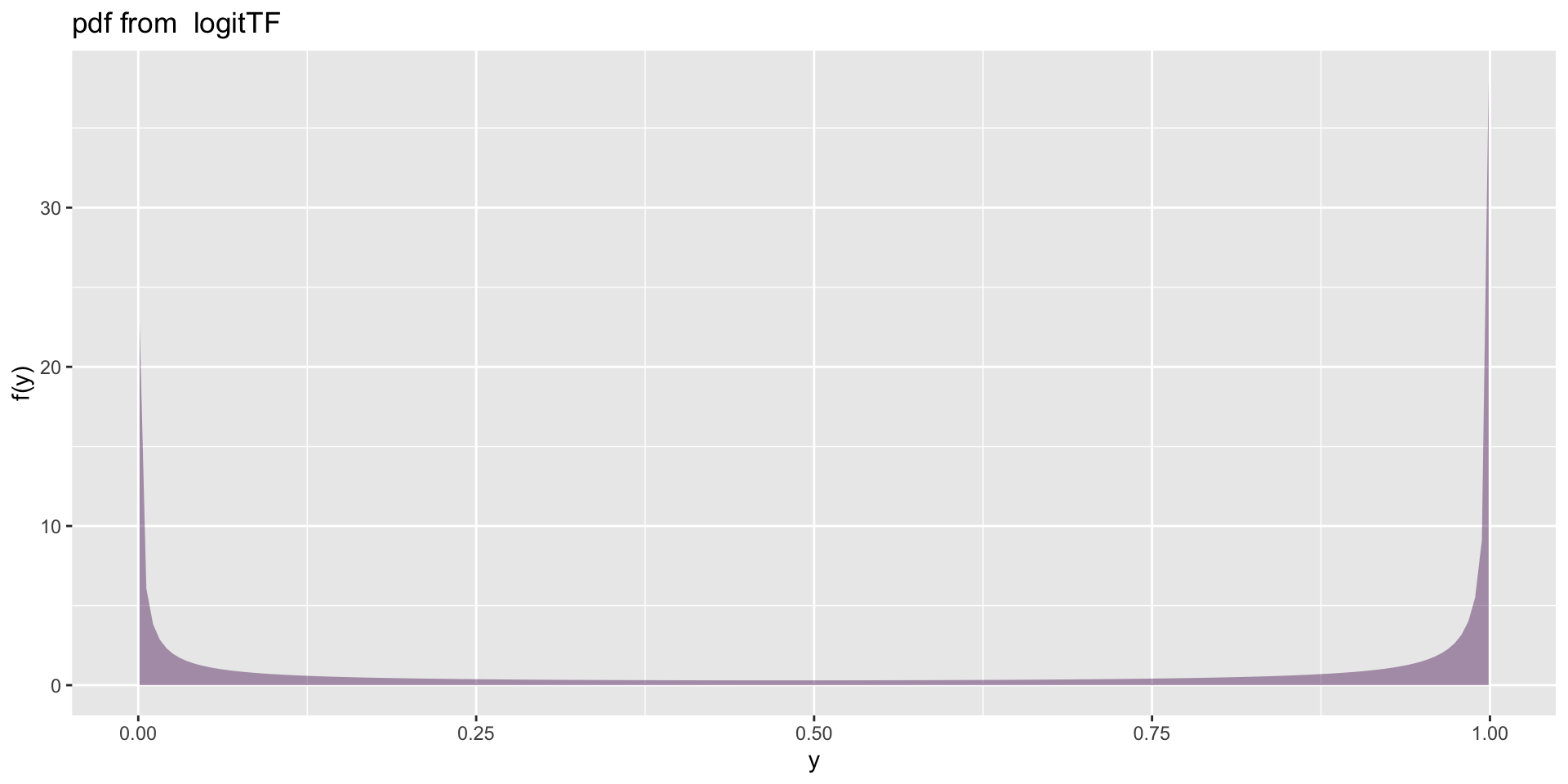 
family_pdf("logitTF", from=0.001, to=.999, mu=0, sigma=1, nu=5)

inflated distributions

A  logit  family of distributions from SHASHo has been generated 
 and saved under the names:  
 dlogitSHASHo plogitSHASHo qlogitSHASHo rlogitSHASHo logitSHASHo 
A  0to1 inflated logitSHASHo distribution has been generated 
 and saved under the names:  
 dlogitSHASHoInf0to1 plogitSHASHoInf0to1 qlogitSHASHoInf0to1 rlogitSHASHoInf0to1 
 plotlogitSHASHoInf0to1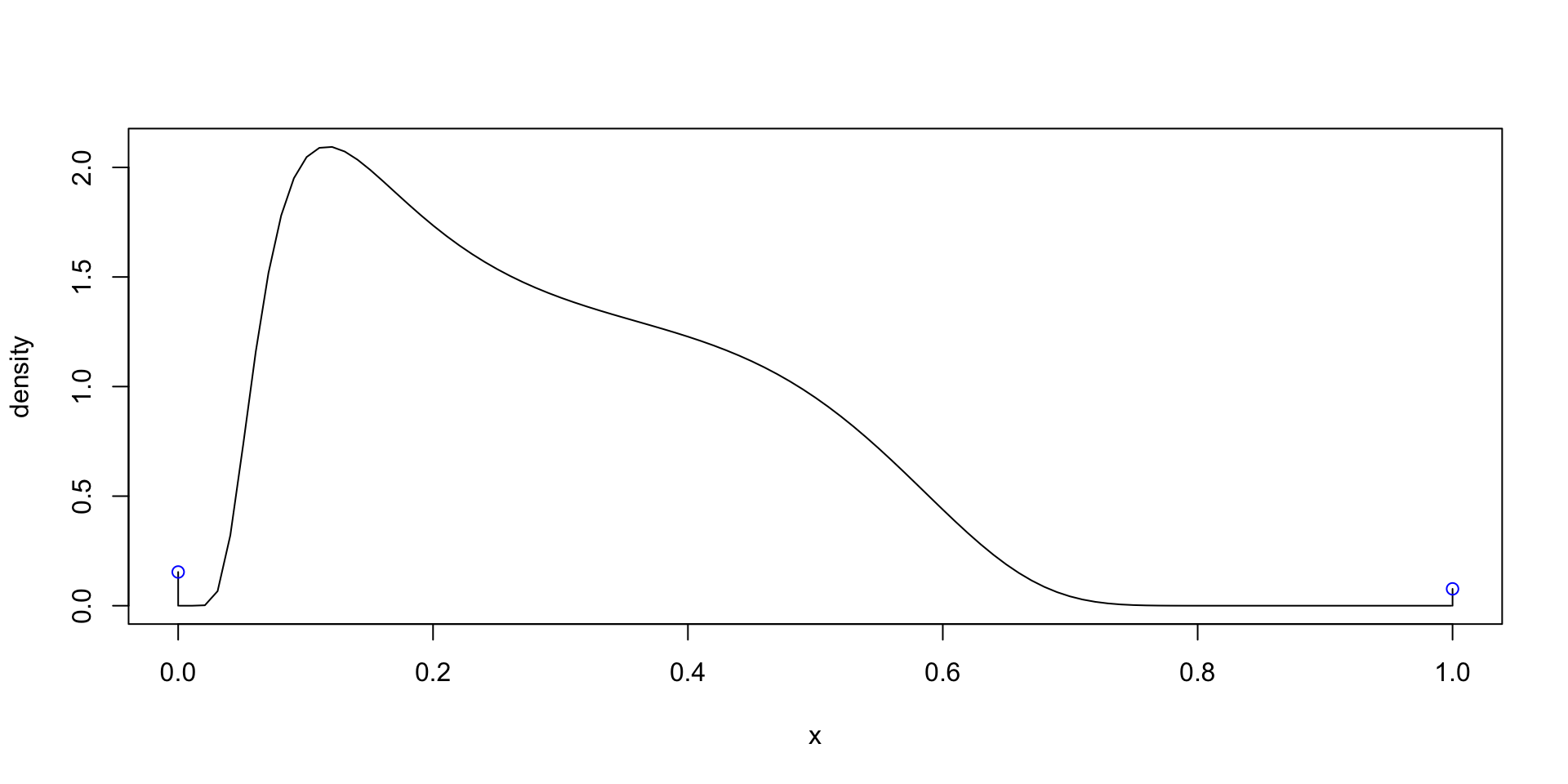

zero adjusted

A zero adjusted BCT distribution has been generated 
 and saved under the names:  
 dBCTZadj pBCTZadj qBCTZadj rBCTZadj 
 plotBCTZadj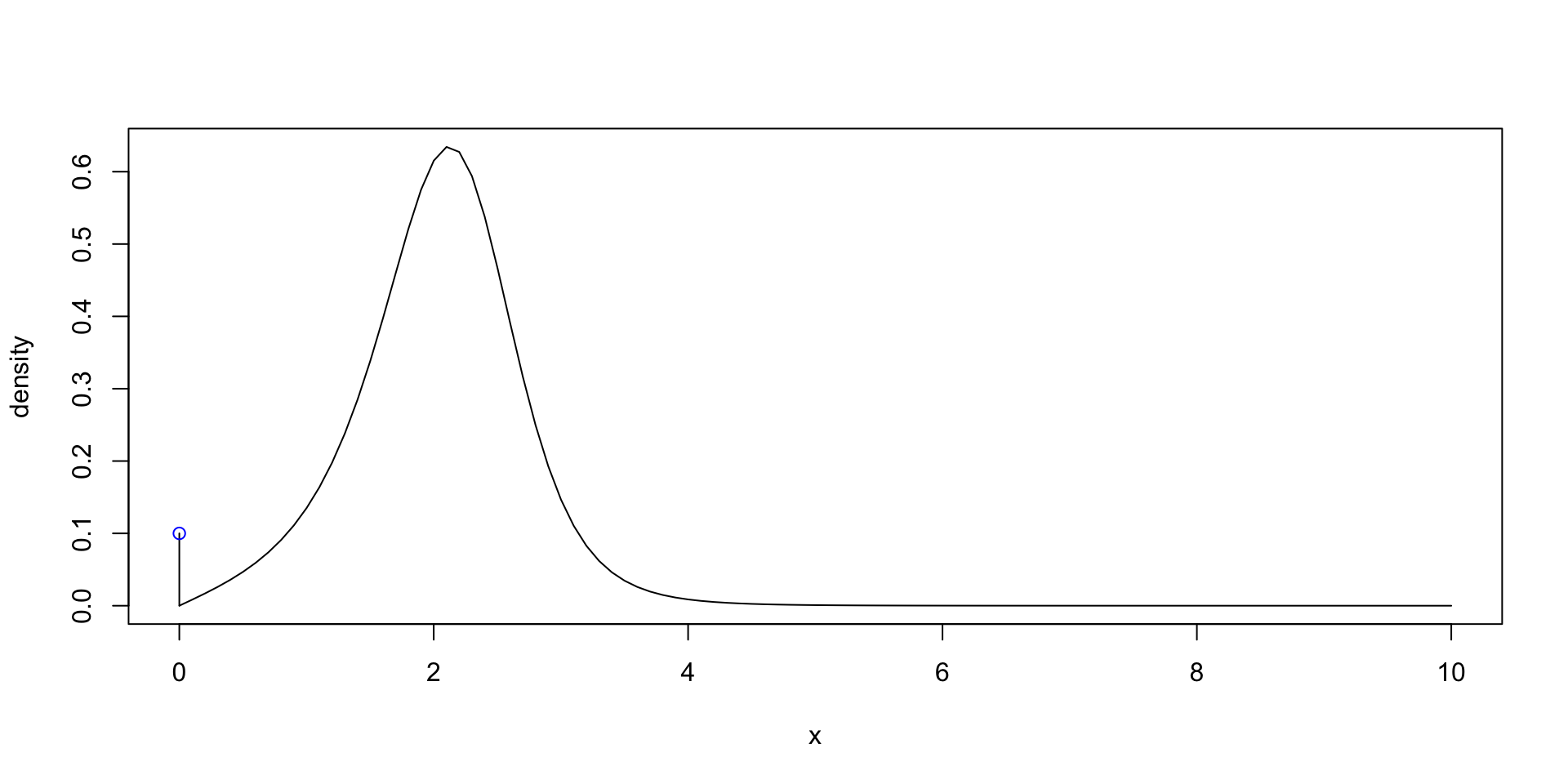

TOBIT

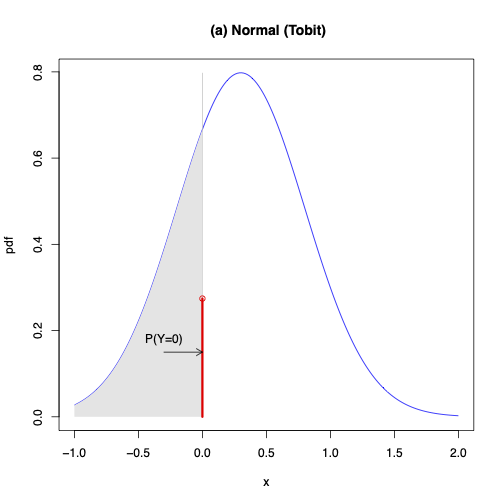
generalized TOBIT

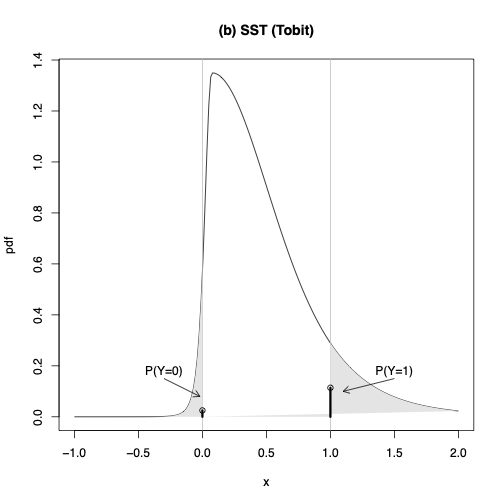
book 2

book2

end

back to the index

The Books

www.gamlss.com