Discrete Distributions

Mikis Stasinopoulos
Bob Rigby
Fernanda De Bastiani
Gillian Heller
Niki Umlauf

Types

  • discrete count distributions defined on \(0,1,\ldots,\infty\); Poison type or infinity count discrete distributions

  • discrete count distributions defined on \(0,1,\ldots,n\); binomial type of finite count discrete distributions

infinite count

infinite count discrete

The three major problems encounter when modelling count data using the Poisson distribution.

  • overdispersion
  • excess (or shortage) of zero values
  • long tails (rare events)

flow chart

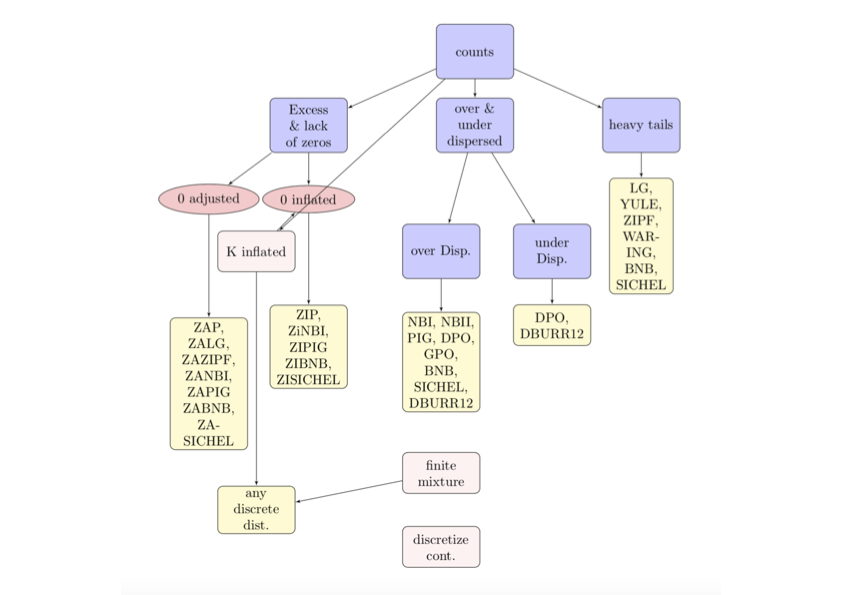
Discrete infinity count distribut.

No Param. Modelling Distributions
1 Location GEOM, LG, PO, YULE
2 Location and scale DPO, GPO, NBI, NBII, PIG, WARING
2 Location and zero probability ZALG, ZAP, ZAZIPF, ZIP, ZIP2
3 Location, scale and skewness BNB, DEL, NBF, SI, SICHEL
3 Location, scale and zero probability ZANBI, ZAPIG, ZINBI, ZIPIG
4 Location, scale, skewness and zero probability ZANBF, ZABNB, ZASICHEL, ZINBF, ZIBNB, ZISICHEL

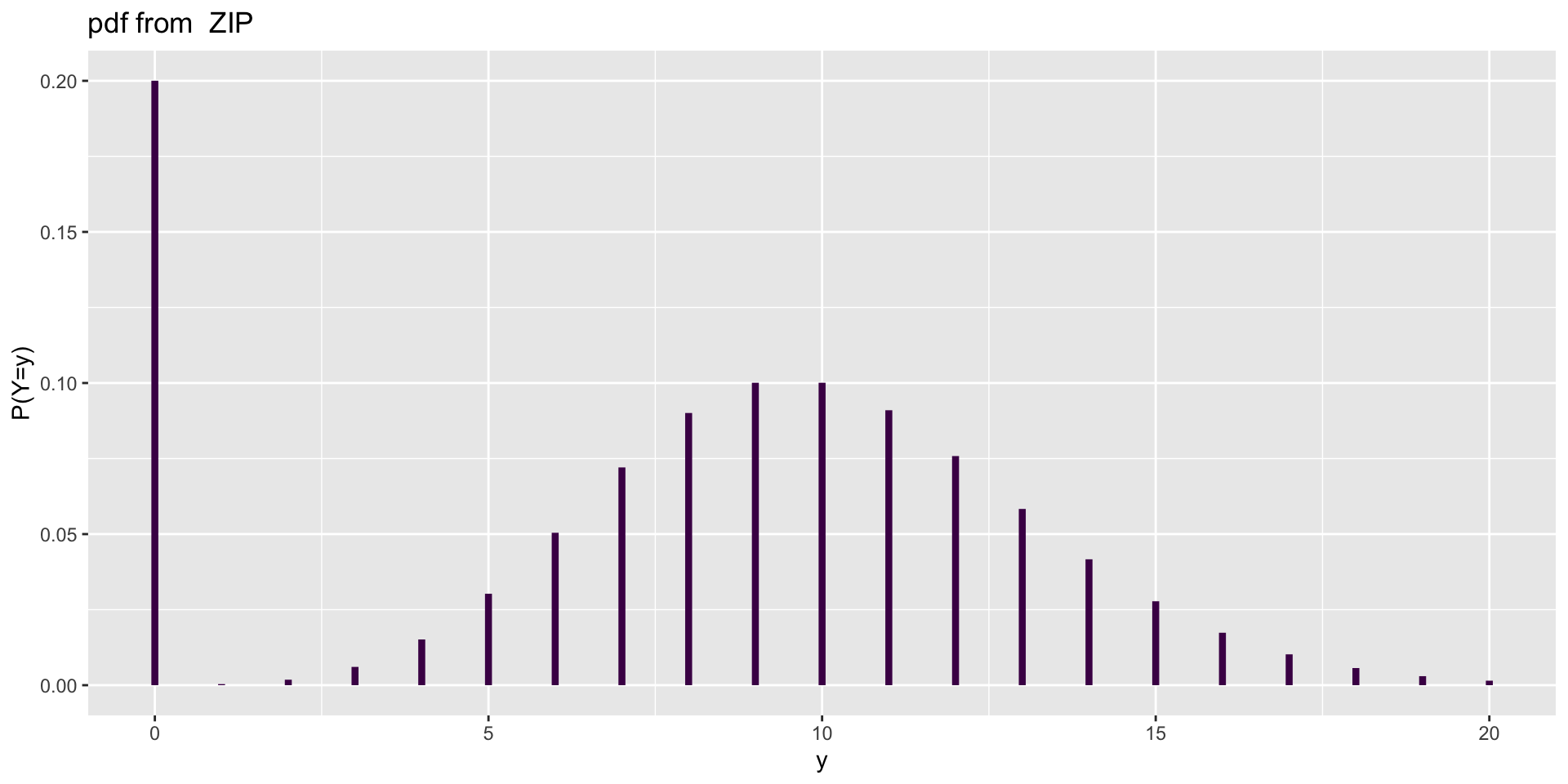
Different types of count (ZIP)

library(gamlss.ggplots)
family_pdf(ZIP, mu=10, sigma=.2, from=0, to=20)

Different types of count (NBI)

family_pdf(NBI, mu=5, sigma=1, from=0, to=20)

Different types of count (NBItr)

library(gamlss.tr)
gen.trun(par=0, family="NBI")
A truncated family of distributions from NBI has been generated 
 and saved under the names:  
 dNBItr pNBItr qNBItr rNBItr NBItr 
The type of truncation is left 
 and the truncation parameter is 0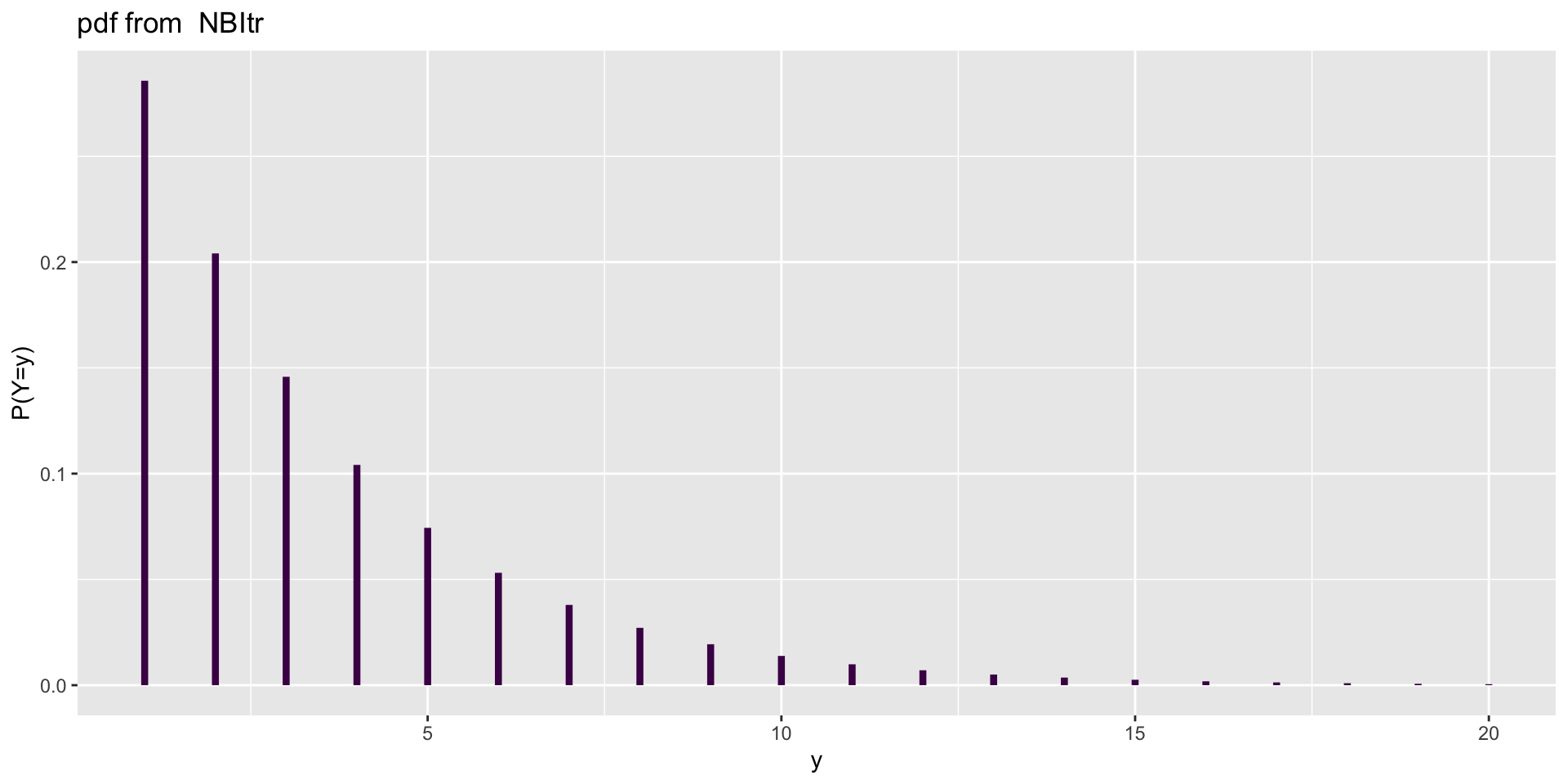  
family_pdf(NBItr, mu=3, sigma=2.5, from=1, to=20)

Different types of count (PIG)

family_pdf(PIG, mu=5, sigma=2, from=1, to=20)

Zero inflated

Zero inflated distribution, \(Y \sim {\bf ZID}\) is given by

\(Y=0\) with probability \(p\)

\(Y \sim {\bf D}\) with probability \(1-p\).

Hence

\[ \begin{split} P(Y=y) &= p + (1-p)P(Y_1=0) & \mbox{if $y=0$} \\ &= (1-p) P(Y_1=y) & \mbox{if $y=1,2,3,...$} \\ \end{split}\]

where \(Y_1 \sim {\bf D}\).

Zero adjusted

Zero adjusted distribution, \(Y \sim {\bf ZAD}\) is given by

\(Y=0\) with probability \(p\)

\(Y \sim {\bf Dtr}\) with probability \(1-p\),

where \({\bf Dtr}\) is a truncated distribution, \({\bf D}\) truncated at zero.

Hence

\[ \begin{split} P(Y=y) &= p & \mbox{if $y=0$} \\ &= (1-p) \frac{P(Y_1=y)}{1-P(Y_1=0)} & \mbox{if $y=1,2,3,...$} \\ \end{split}\]

where \(Y_1 \sim {\bf D}\).

Oversispersion and underdispersion

Types of overdispersion

  1. Ad-hoc solutions

    (i) quasi-likelihood (QL),  Extended QL

(ii) Efron's Double Exponential

(iii) pseudo-likelihood (PL)

  2. Discretized continuous distributions for example if \(F_W(w)\) is the cdf a continuous random variable \(W\) defined in \(\Re^+\) then \[f_Y(y)=F_W(y+1)-F_W(y)\]

  3. Random effect at the observation level solutions. \(f_Y(y)=\int f(y|\gamma) f_{\gamma}(\gamma) d\gamma\).

random effect at observation level

  1. when an an explicit continuous mixture distribution, \(f_Y(y)\), exists.

  2. when a continuous mixture distribution, \(f_Y(y)\), is not explicit but is approximated by integrating out the random effect using approximations, e.g. Gaussian quadrature or Laplace approximation.

  3. when a non-parametric mixture (effectively a finite mixture) is assumed for the response variable.

random effect at observation level

Explicit continuous mixture distribution

\[ \underbrace{f_Y(y)}_\text{discrete}= \int \underbrace{f(y|\gamma)}_\text{discrete} \underbrace{ f_{\gamma}(\gamma)}_\text{continuous} d\gamma \]

  • \(Y\sim NBI(\mu,\sigma)\)
  • \(Y|\gamma \sim PO(\gamma \mu )\)
  • \(\gamma \sim GA(1, \sigma^{1/2})\)

random effect at observation level II

Parametric mixture distribution

\[ \underbrace{f_Y(y)}_\text{discrete}= \int \underbrace{f(y|\gamma)}_\text{discrete} \underbrace{ f_{\gamma}(\gamma)}_\text{continuous} d\gamma \]

  • \(Y\sim PO-Normal(\mu,\sigma)\)

  • \(Y|\gamma \sim PO(\gamma \mu)\)

  • \(\log(\gamma) \sim NO(1, \sigma)\)

random effect at observation level III

Non-parametric mixture distribution {.smaller}

\[ \underbrace{f_Y(y)}_\text{discrete}= \sum_{k=1}^{K} \underbrace{f(y| \gamma_k)}_\text{discrete} \underbrace{ p(\gamma=\gamma_k)}_\text{continuous} \]

  • \(Y\sim PO-NPFM(\mu,\sigma)\)

  • \(Y|\gamma \sim PO({\gamma \mu})\)

  • \(\log(\gamma) \sim NPFM(2)\)

where NPFM(2) equals Non-Parametric Finite Mixture with 2 point probabilities

explicit continuous Mixtures

Distributions R Name mixing distribution for \(\gamma\)
Poisson PO\((\mu)\) -
Neg. bin. I NBI\((\mu,\sigma)\) GA\((1,\sigma^{\frac{1}{2}}\))
Neg. bin. II NBII\((\mu,\sigma)\) GA\((1,\sigma^{\frac{1}{2}}/\mu)\)
Poisson IG PIG\((\mu,\sigma)\) IG\((1,\sigma^{\frac{1}{2}})\)
Sichel SICHEL\((\mu,\sigma,\nu)\) GIG\((1,\sigma^{\frac{1}{2}},\nu)\)
Delaporte DEL\((\mu,\sigma,\nu)\) SG\((1,\sigma^{\frac{1}{2}},\nu)\)
Zero inf. Poisson ZIP\((\mu,\sigma)\) BI\((1,1-\sigma)\)
Zero inf. Poisson 2 ZIP2\((\mu,\sigma)\) \((1-\sigma)^{-1}\)\((1,1-\sigma)\)
Zero inf. neg. bin. \((\mu,\sigma, \nu)\) zero inflated gamma
Poisson-Tweedie - Tweedie family

mean and variance

R Name params mean variance
PO\((\mu)\) 1 \(\mu\) \(\mu\)
NBI\((\mu,\sigma)\) 2 \(\mu\) \(\mu+\sigma\mu^2\)
NBII\((\mu,\sigma)\) 2 \(\mu\) \(\mu+\sigma\mu\)
PIG\((\mu,\sigma)\) 2 \(\mu\) \(\mu+\sigma\mu^2\)
SICHEL\((\mu,\sigma,\nu)\) 3 \(\mu\) \(\mu+h(\sigma,\nu)\mu^2\)
DEL\((\mu,\sigma,\nu)\) 3 \(\mu\) \(\mu+\sigma(1-\nu)^2\mu^2\)
ZIP\((\mu,\sigma)\) 2 \((1-\sigma)\mu\) \((1-\sigma)\mu+\sigma(1-\sigma)\mu^2\)
ZIP2\((\mu,\sigma)\) 2 \(\mu\) \(\mu+ \frac{\sigma}{(1-\sigma)} \mu^2\)

nagative binomial Family

  • Negative Binomial type I: \[V \left[ Y \right]= \mu + \sigma \mu^2 \]
  • Negative Binomial type II: \[V \left[ Y \right]= \mu + \sigma \mu\]
  • Negative Binomial family \[V(Y)=\mu+\sigma \mu^{\nu}\]

finite count

Binomial type

Distribution name links
\(\mu\) \(\sigma\) \(\nu\) \(\tau\)
binomial BI logit - - -
beta binomial BB logit log - -
double binomial DBI logit log - -
zero-adj beta binomial ZABB logit log logit -
zero-adj binomial ZABI logit logit - -
zero-inf beta binomial ZABB logit log logit -
zero-inf binomial ZIBI logit logit - -

examples

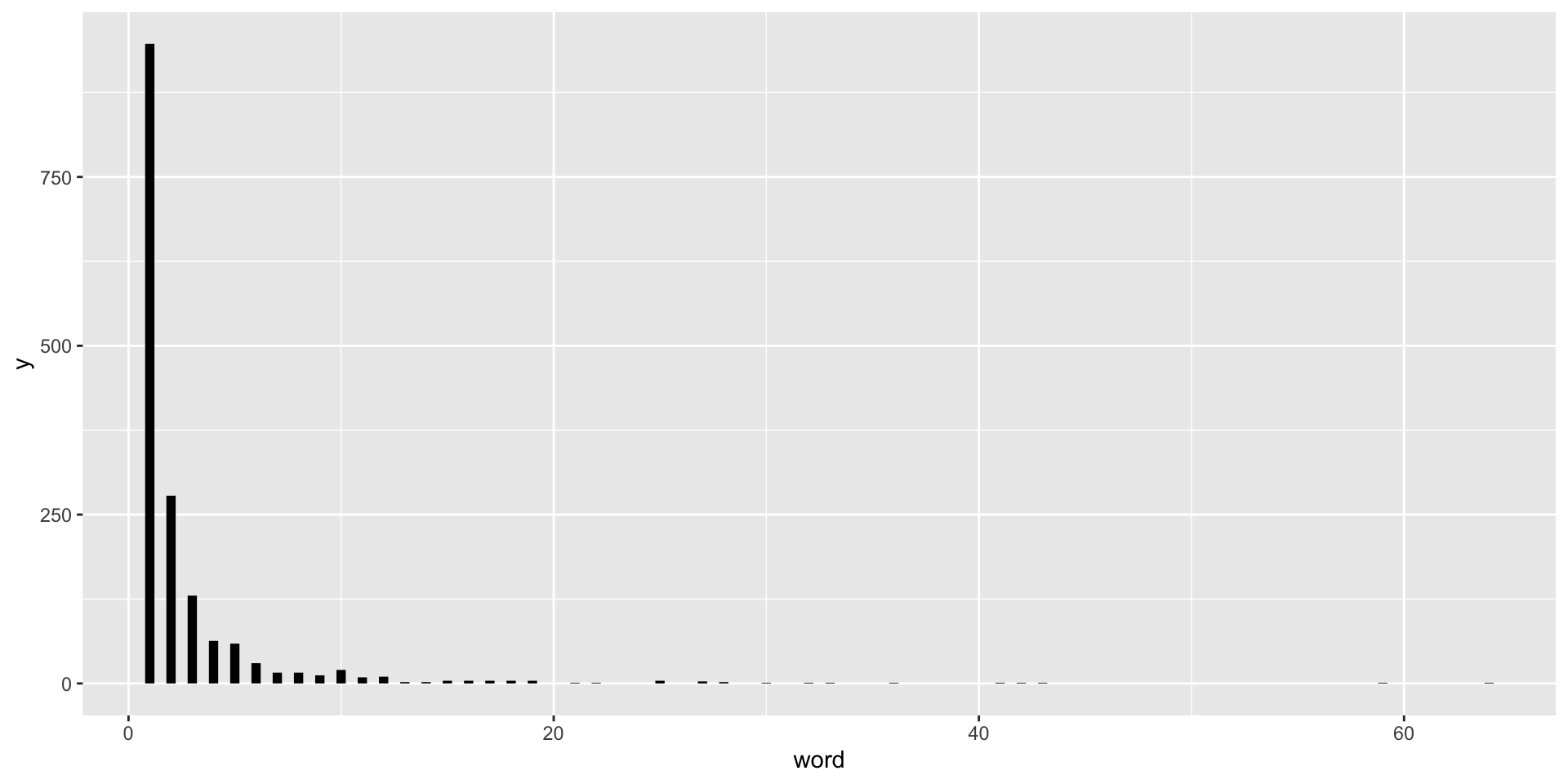
stylometric: data

Data summary: R data file: stylo in package gamlss.data of dimensions $ 64 $ - source: Dr Mario Corina-Borja

  • word: is the number of times a word appears in a single text

  • freq: the frequency of the number of times a word appears in a text

  • purpose: to demonstrate the fitting of a truncated discrete dist.

  • conclusion: the truncated SICHEL distributions fits best

stylometric: plot (con.)

library(ggplot2)
library(gamlss)
ggplot(data=stylo, aes(x=word, xend = word, y = 0, yend=freq))+
  geom_segment(lwd=2)

stylometric: truncation (con.)

library(gamlss.tr)
gen.trun(par = 0, family = PO, type = "left")
A truncated family of distributions from PO has been generated 
 and saved under the names:  
 dPOtr pPOtr qPOtr rPOtr POtr 
The type of truncation is left 
 and the truncation parameter is 0  
gen.trun(par = 0, family = NBII, type = "left")
A truncated family of distributions from NBII has been generated 
 and saved under the names:  
 dNBIItr pNBIItr qNBIItr rNBIItr NBIItr 
The type of truncation is left 
 and the truncation parameter is 0  
gen.trun(par = 0, family = DEL, type = "left")
A truncated family of distributions from DEL has been generated 
 and saved under the names:  
 dDELtr pDELtr qDELtr rDELtr DELtr 
The type of truncation is left 
 and the truncation parameter is 0  
gen.trun(par = 0, family = SICHEL, type = "left",
     delta = 0.001)
A truncated family of distributions from SICHEL has been generated 
 and saved under the names:  
 dSICHELtr pSICHELtr qSICHELtr rSICHELtr SICHELtr 
The type of truncation is left 
 and the truncation parameter is 0

stylometric: fits (con.)

library(gamlss2)
mPO <- gamlss2(word ~ 1, weights = freq, data = stylo, family = POtr, 
trace = FALSE)
mNBII <- gamlss2(word ~ 1, weights = freq, data = stylo, family = NBIItr, 
n.cyc = 50, trace = FALSE)
mDEL <- gamlss2(word ~ 1, weights = freq, data = stylo, family = DELtr, 
n.cyc = 50, trace = FALSE)
mSI <- gamlss2(word ~ 1, weights = freq, data = stylo, family = SICHELtr, 
n.cyc = 50, trace = FALSE)
gamlss2::GAIC(mPO, mNBII, mDEL, mSI)
           AIC df
mSI   5149.054  3
mDEL  5160.706  3
mNBII 5322.344  2
mPO   9207.459  1

stylometric: fitted POtr (con.)

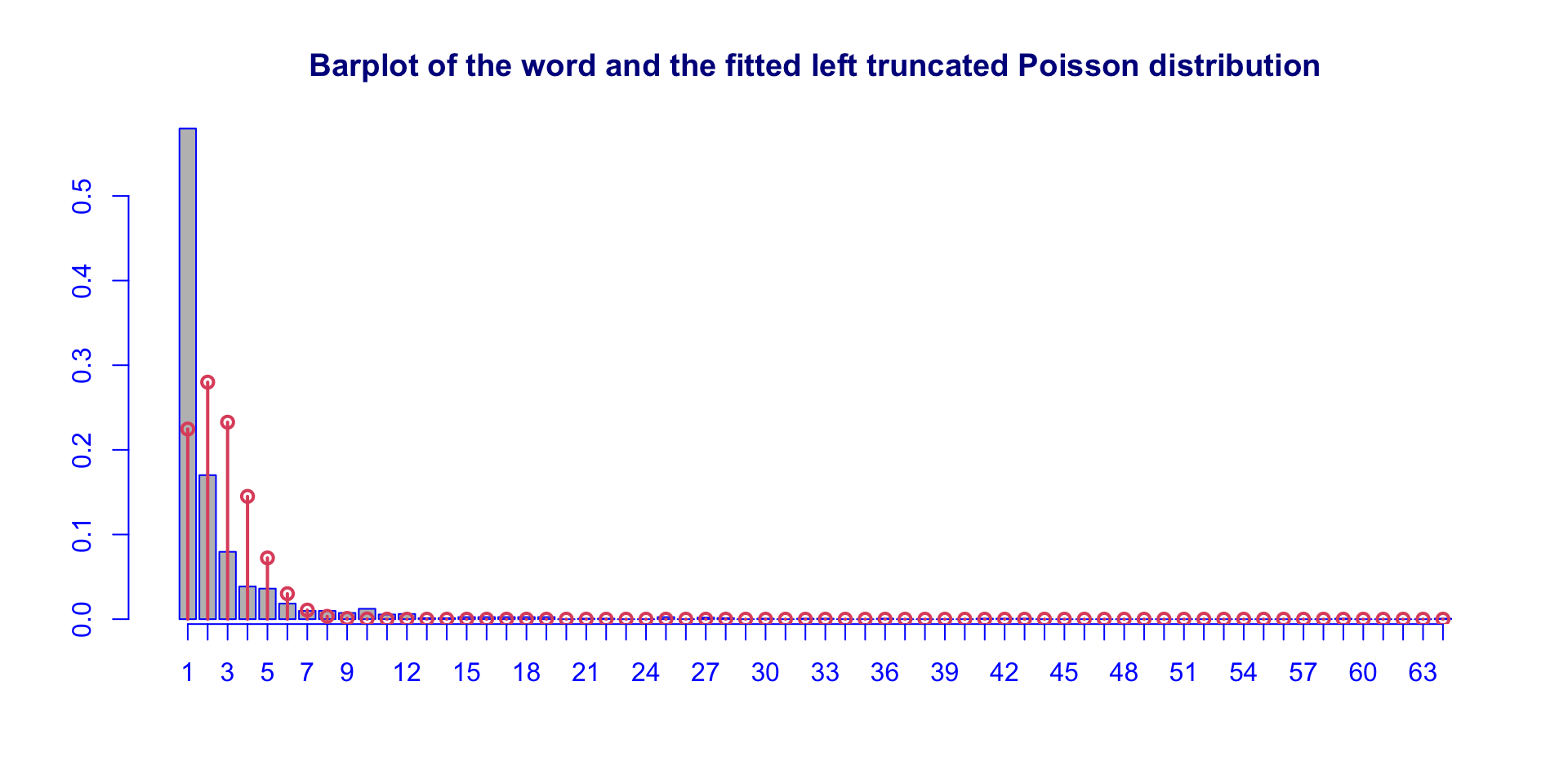
m1 <- histDist(word, data=stylo, freq=freq, family=POtr)

stylometric: fitted NBIItr (con.)

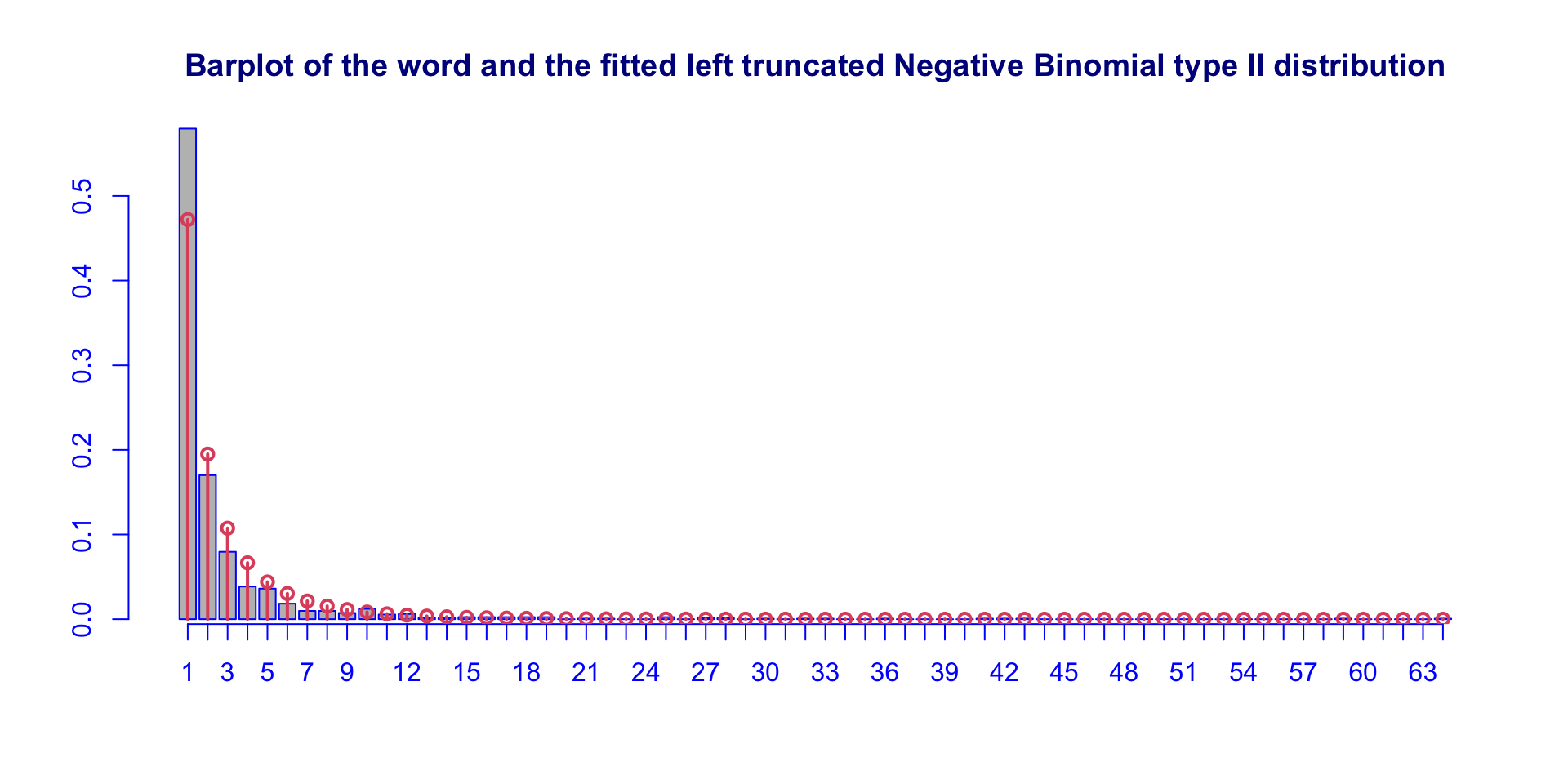
m1 <- histDist(word, data=stylo,  freq=freq, family=NBIItr)

stylometric: fitted DELtr (con.)

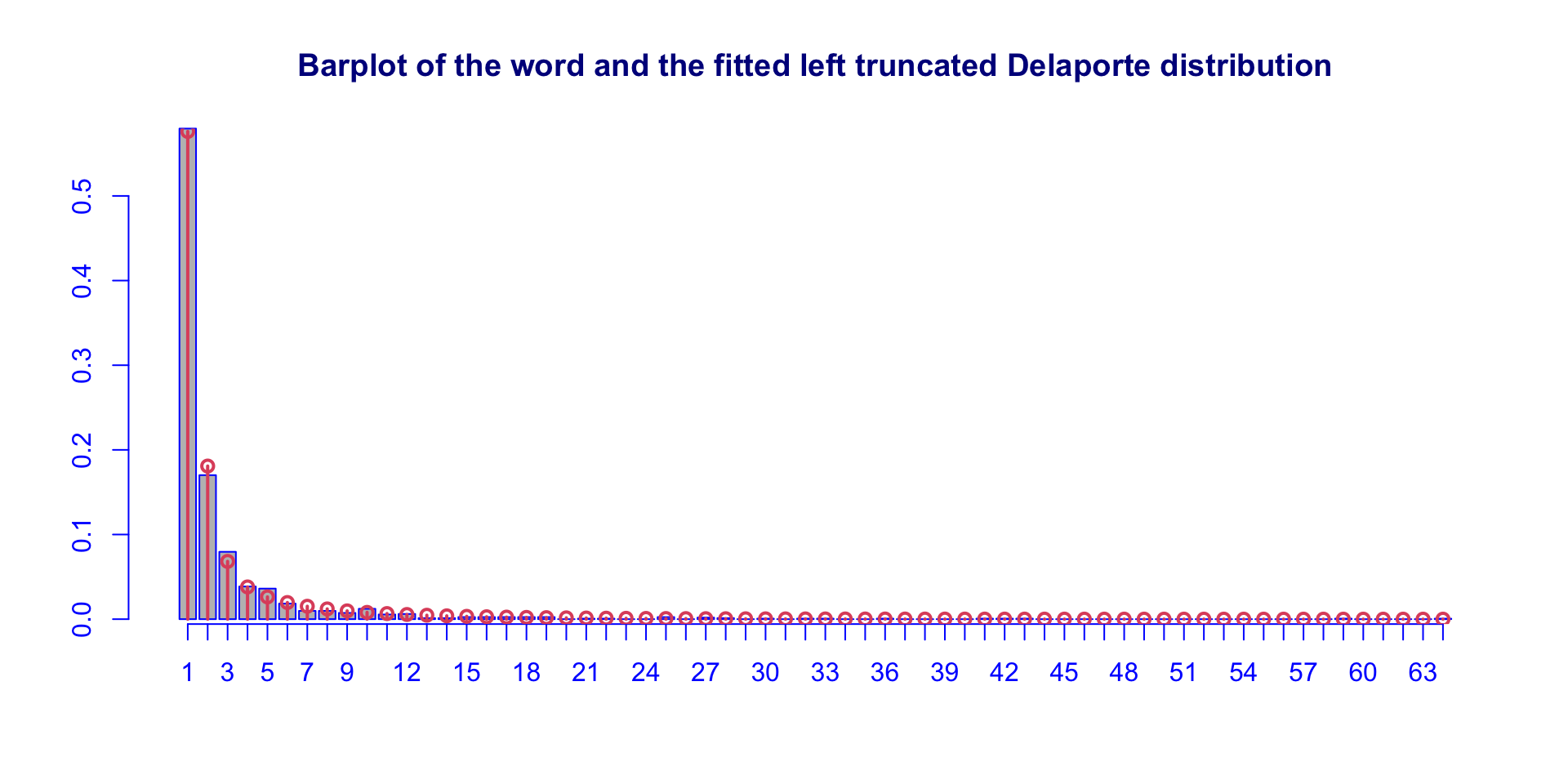
m1 <- histDist(word, data=stylo,  freq=freq, family=DELtr)

stylometric: fitted SICHELtr (con.)

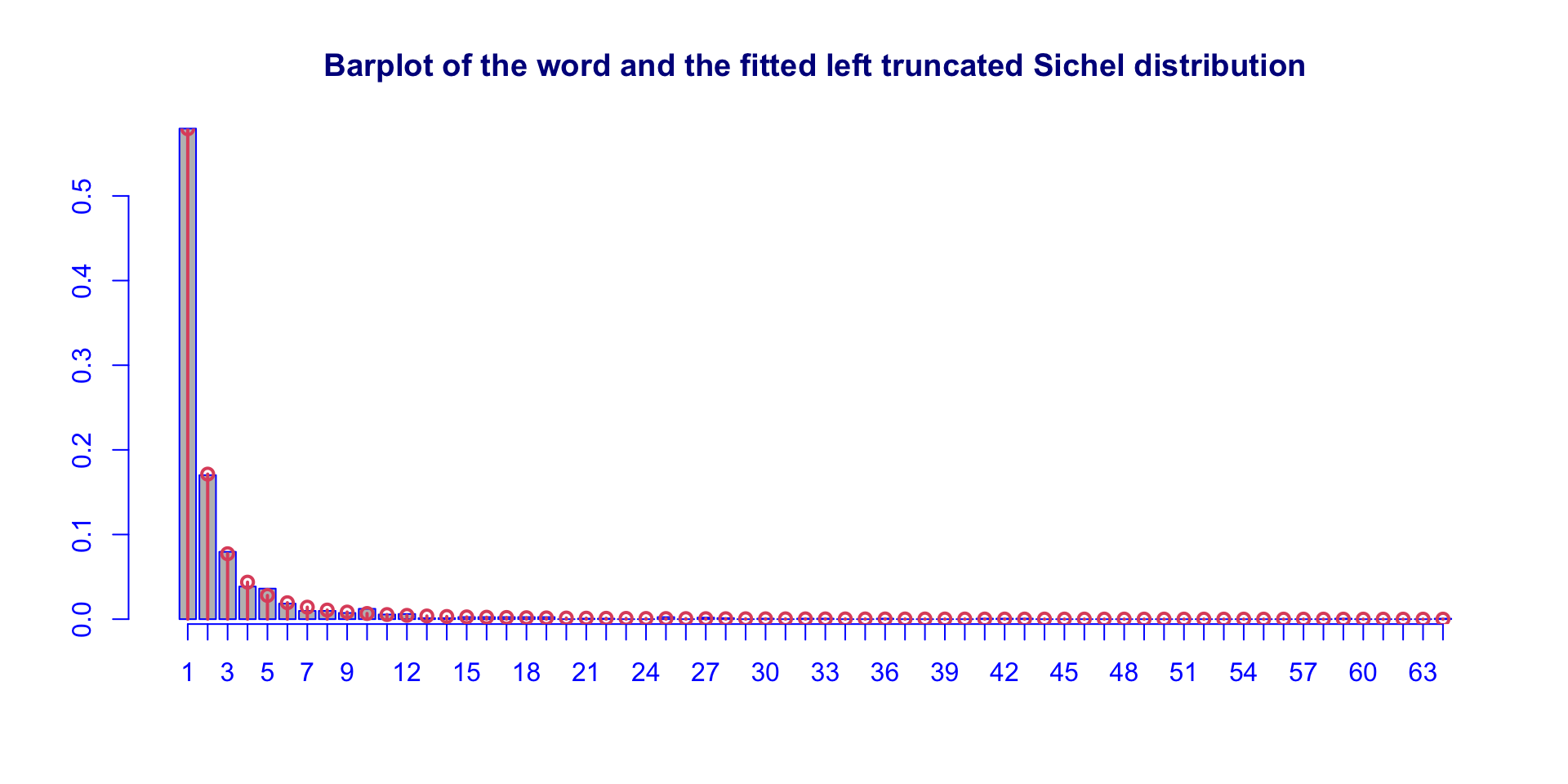
m1 <- histDist(word, data=stylo,  freq=freq, family=SICHELtr)

fish species data

  • R data file: species in package gamlss.data of dimensions \(70 \times 2\)

  • variables

    • fish: the number of different species in 70 lakes in the world
    • lake: the lake area

fish species plot

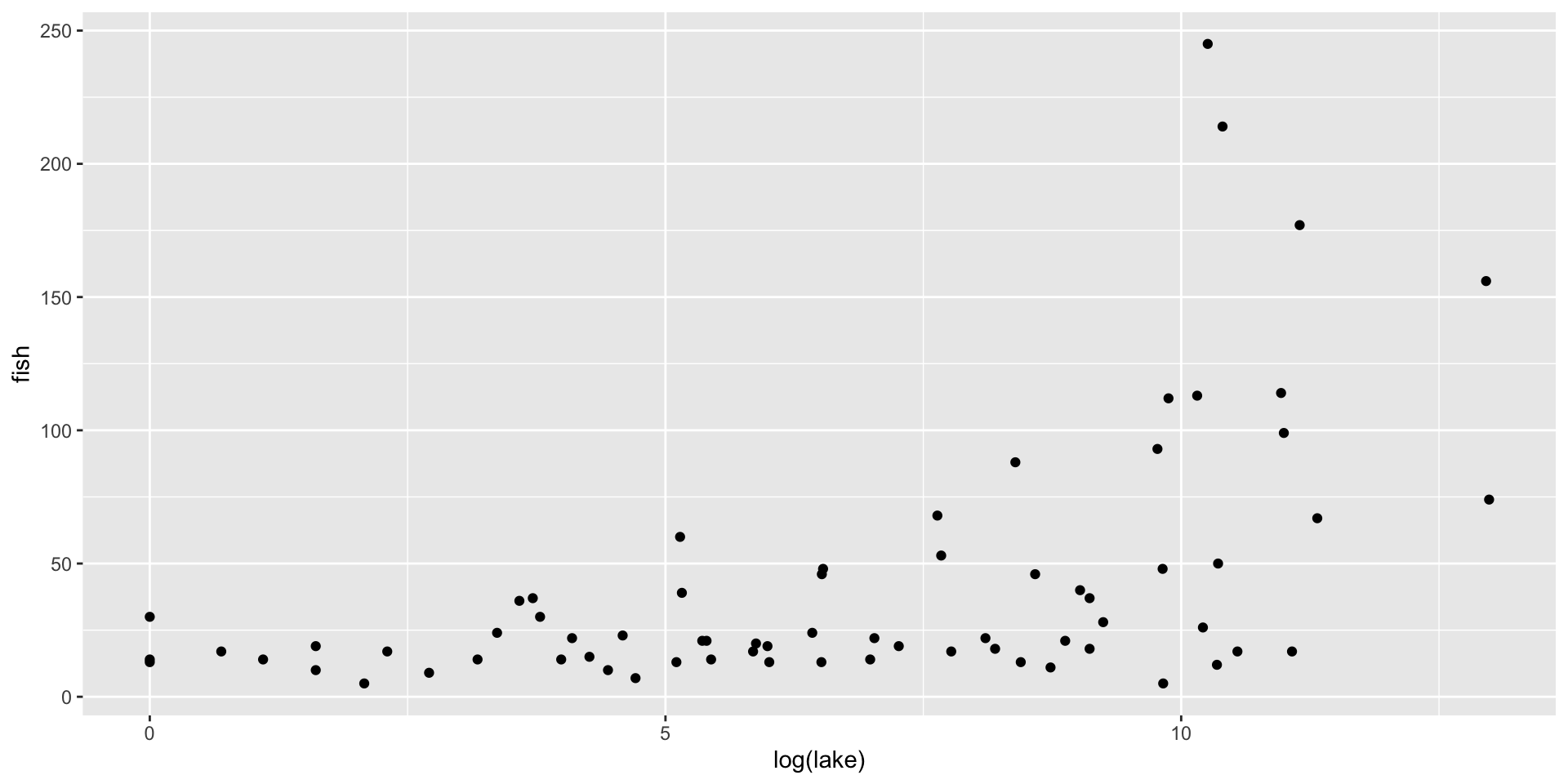
fish species questions

  • How does the mean of \(y\) depend on \(x\)?
  • Is \(y\) overdispersed Poisson?
  • How does the variance \(y\) depend on its mean?
  • What is the distribution of \(y\) given \(x\)?
  • Do the scale and shape parameters of the distribution of \(y\) depend on \(x\)?

fish species fits

Model \(f_Y(y)\) \(\mu\) \(\sigma\) \(\nu\) GDEV df AIC SBC
1 PO poly(x,2) - - 1849.3 3 1855.3 1862.0
2 NBI \(x\) \(1\) - 619.8 3 625.8 632.6
3 NBI poly(x,2) \(1\) - 614.3 4 622.3 631.3
4 NBI s(x) \(1\) - 611.9 6 623.9 637.4
5 NBI poly(x,2) x - 605.0 5 615.0 626.2
6 NBI-fam poly(x,2) 1 1 606.0 5 616.0 627.3
7 NBI-fam poly(x,2) x 1 604.9 6 616.9 630.4
8 PIG poly(x,2) \(1\) - 613.3 4 621.3 630.3
9 SI poly(x,2) \(1\) x 597.7 6 609.7 623.2

fish species fits (con.)

Model \(f_Y(y)\) \(\mu\) \(\sigma\) \(\nu\) GDEV df AIC SBC
10 DEL poly(x,2) 1 x 600.6 6 612.6 626.1
11 DEL poly(x,2) - x 600.6 5 610.6 621.9
12 PO-Normal poly(x,2) 1 - 615.2 4 623.2 632.2
13 NBI-Normal poly(x,2) x \(1\) 603.7 6 615.7 629.2
14 PO-NPFM(5) poly(x,2) - \(-\) 601.9 13 627.9 657.2
15 NB-NPFM(2) poly(x,2) 1 \(-\) 611.9 6 623.9 637.4
16 doublePO poly(x,2) x - 616.4 5 626.4 637.6
17 IGdisc poly(x,2) 1 - 603.3 4 611.3 620.3

fish species fitted mean

library(gamlss2)
m1 <- gamlss2(fish~log(lake), data=species, family=SI, trace=F)
ggplot(data=species, aes(x=log(lake), y=fish))+
geom_point()+
geom_line(aes(y=predict(m1,type="parameter", what="mu")))
#geom_line(aes(y=fitted(m1, type="parameter", what="mu")))

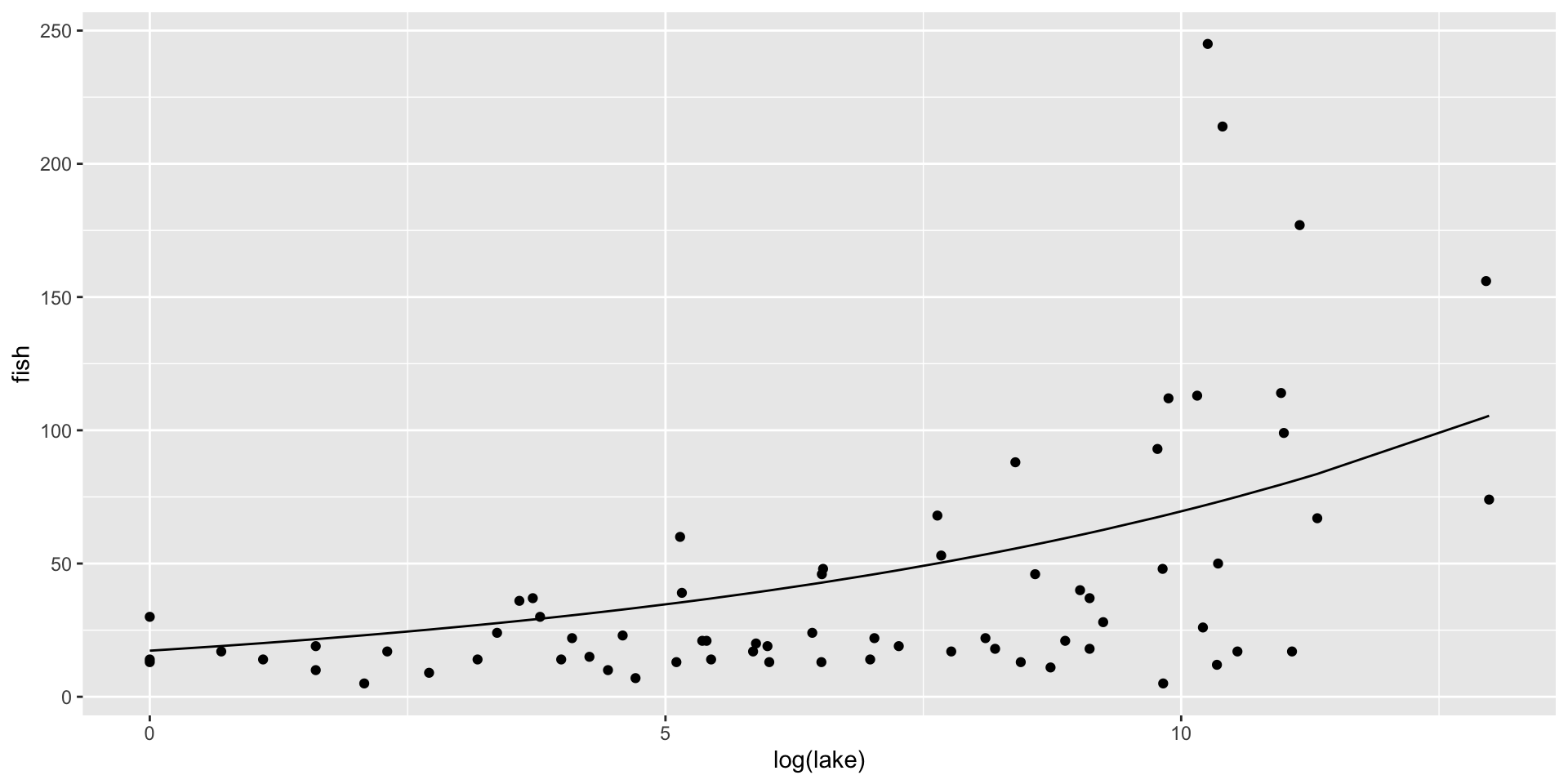
fish species fitted pdf

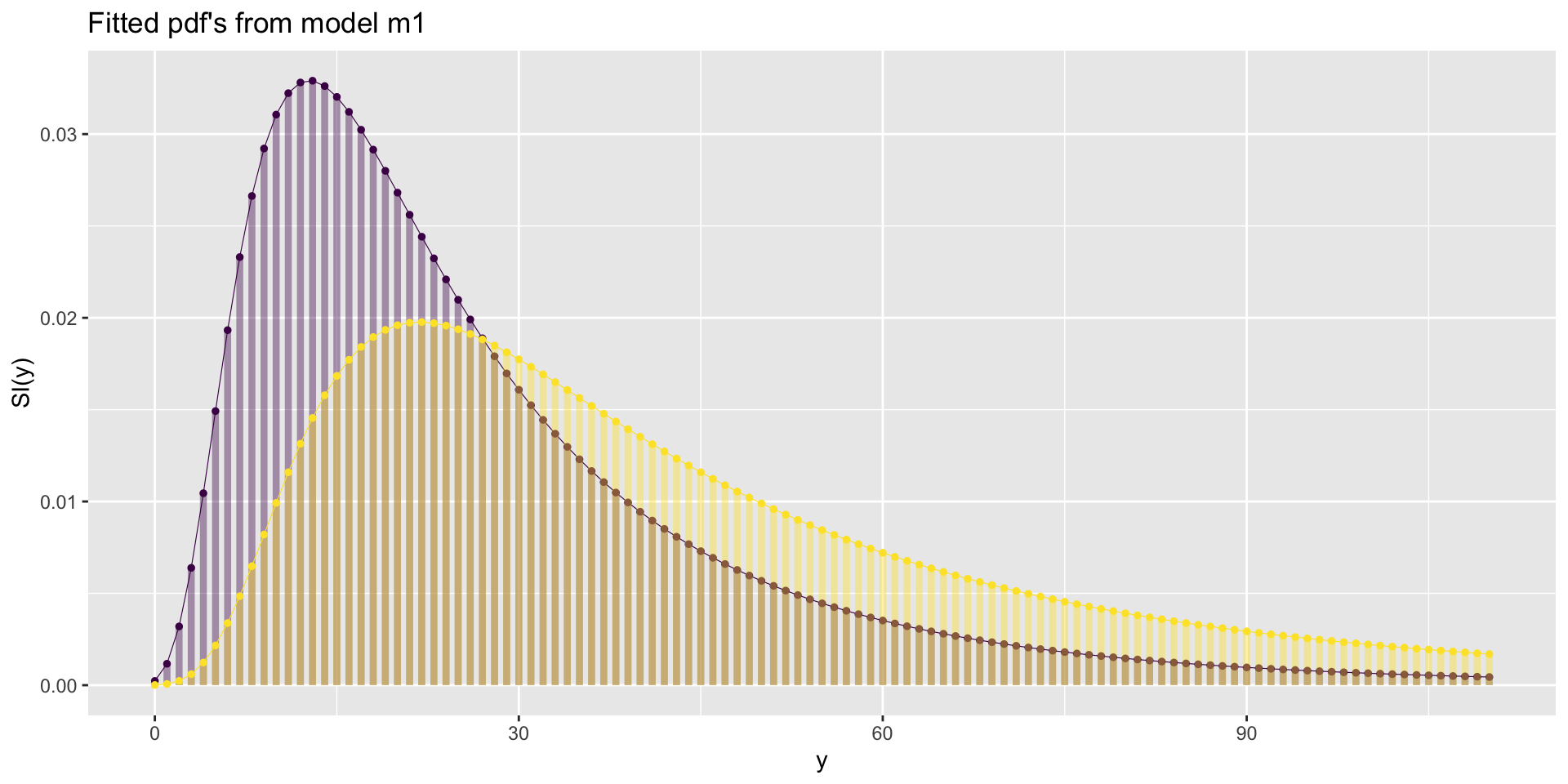
fish species fitted cdf

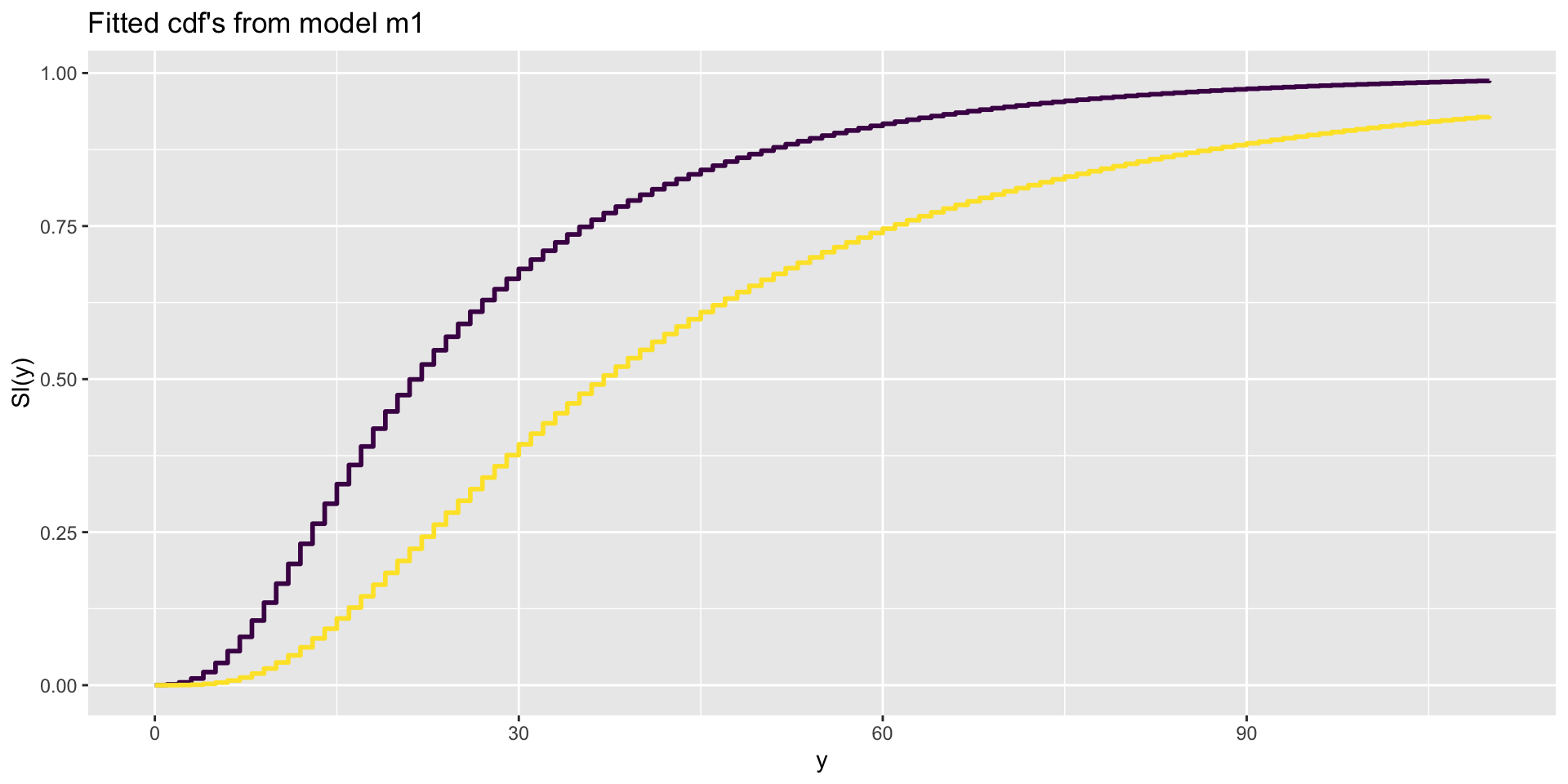
fish species diagnostics

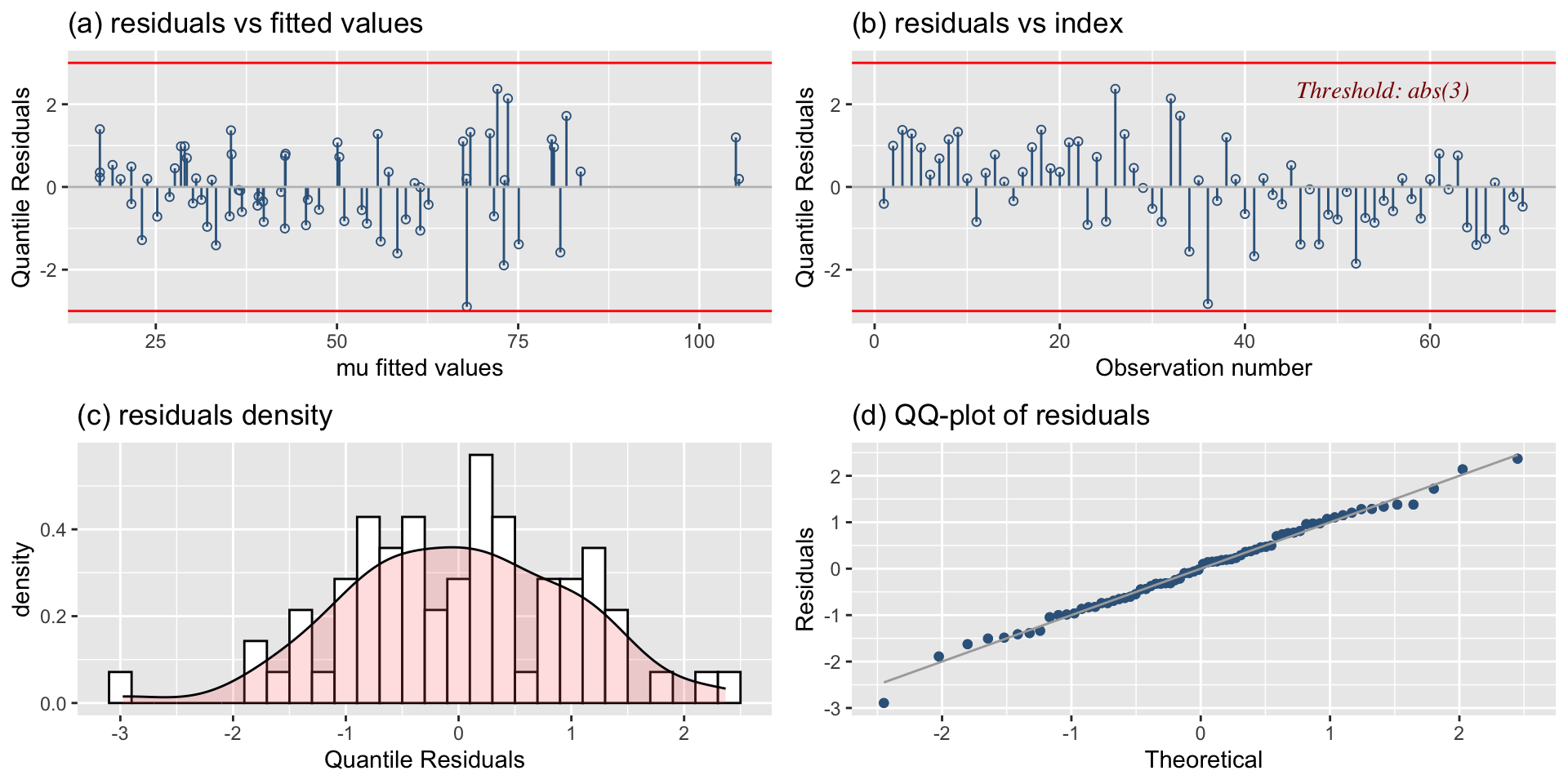
the hospital stay data

library(gamlss.prepdata)
da <- aep[, -c(1,2,3,8,9)]
da$r <- with(aep, noinap/los*100)
data_xyplot(da, response=r)
100 % of data are ploted, 
that is, 1383 observations.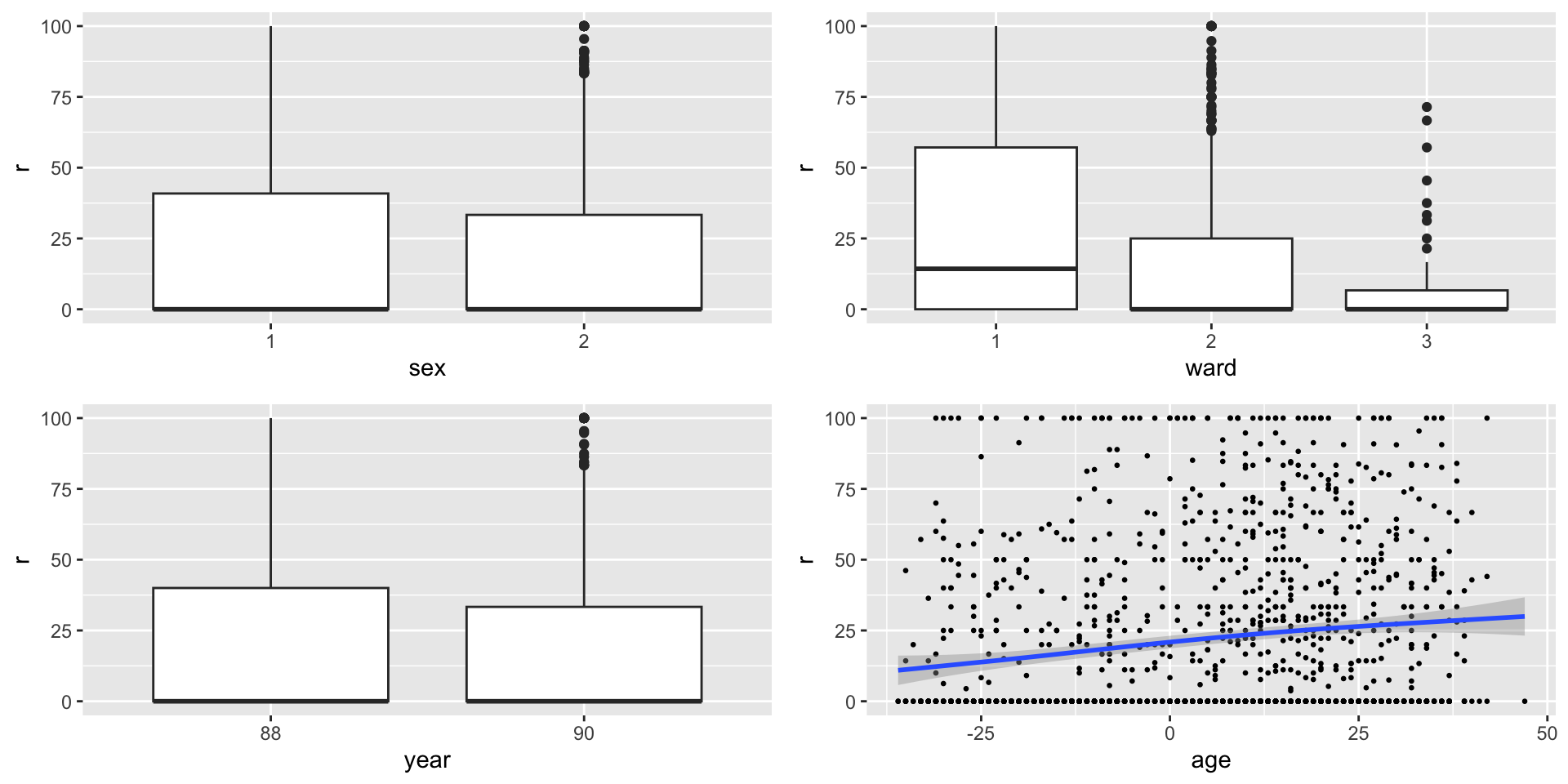

the hospital stay fits

library(gamlss2)
mI <- gamlss2(y ~ ward + year + loglos|year, family = BB, data = aep, trace=F)
mII <- gamlss2(y ~ ward + year + loglos|year + ward, family = BB, 
               data = aep, trace=FALSE)
mIII <- gamlss2(y ~ ward + year + s(loglos)| year+ward, 
              family = BB, data = aep,trace=FALSE)
mIV <- gamlss2(y ~ ward + year + s(loglos)+s(age)| year+ward, 
              family = BB, data = aep,trace=FALSE)
gamlss2::GAIC(mI, mII, mIII, mIV, k = 2)
          AIC       df
mIV  4476.796 15.86038
mIII 4477.800 14.09619
mII  4501.020  9.00000
mI   4533.441  7.00000

the hospital stay fits

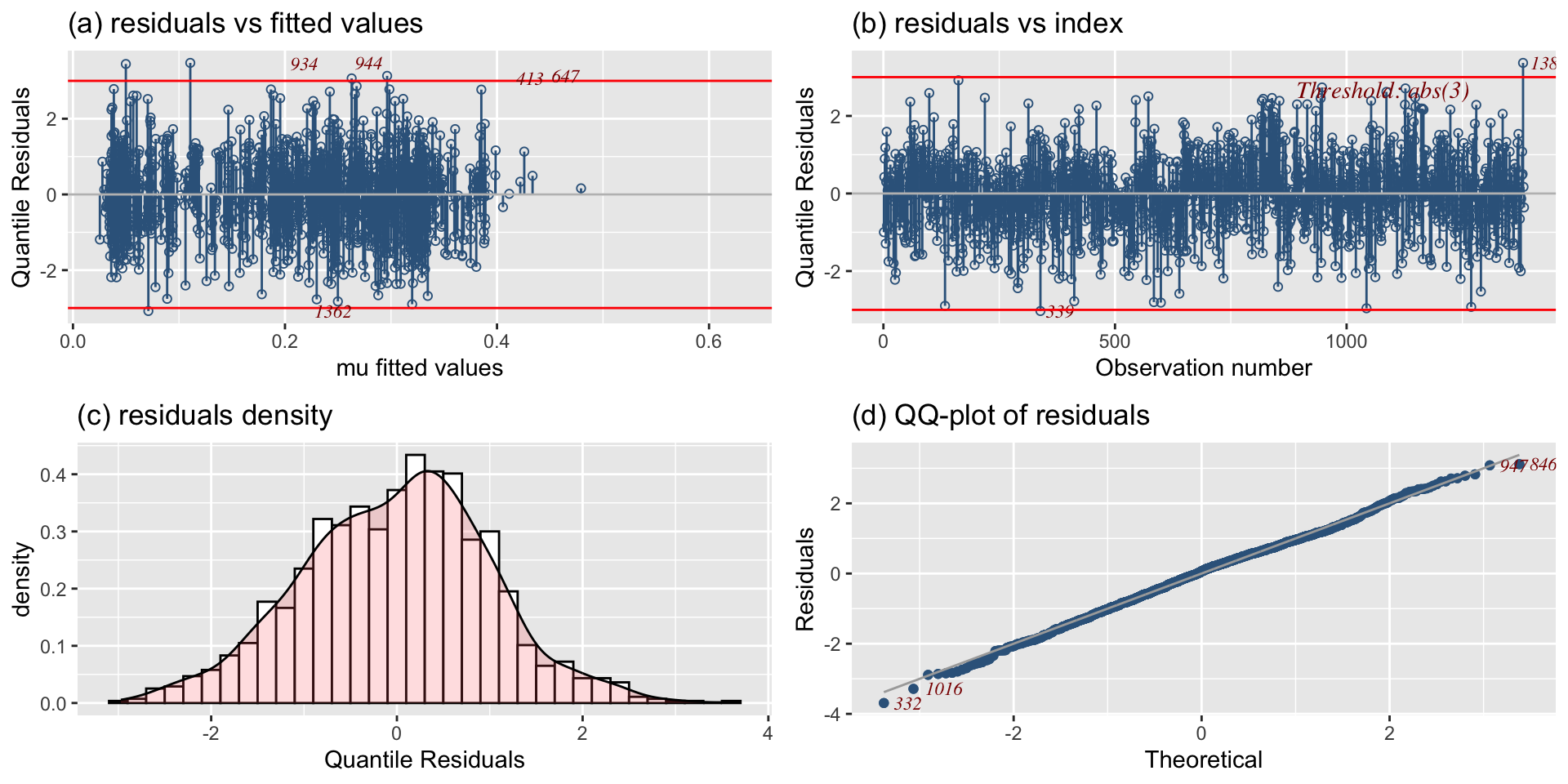
END

back to the index

The Books

www.gamlss.com