Centile estimation

Mikis Stasinopoulos
Bob Rigby
Gillian Heller
Fernanda De Bastiani
Niki Umlauf

Introduction

  • The data

  • the problem

  • the methods

  • the LMS and GAMLSS

  • the procedure

the data

The Dutch boys data Source: Buuren and Fredriks (2001)

  • head: the head head circumference of 7040 boys

  • age: the age in years

the data plot

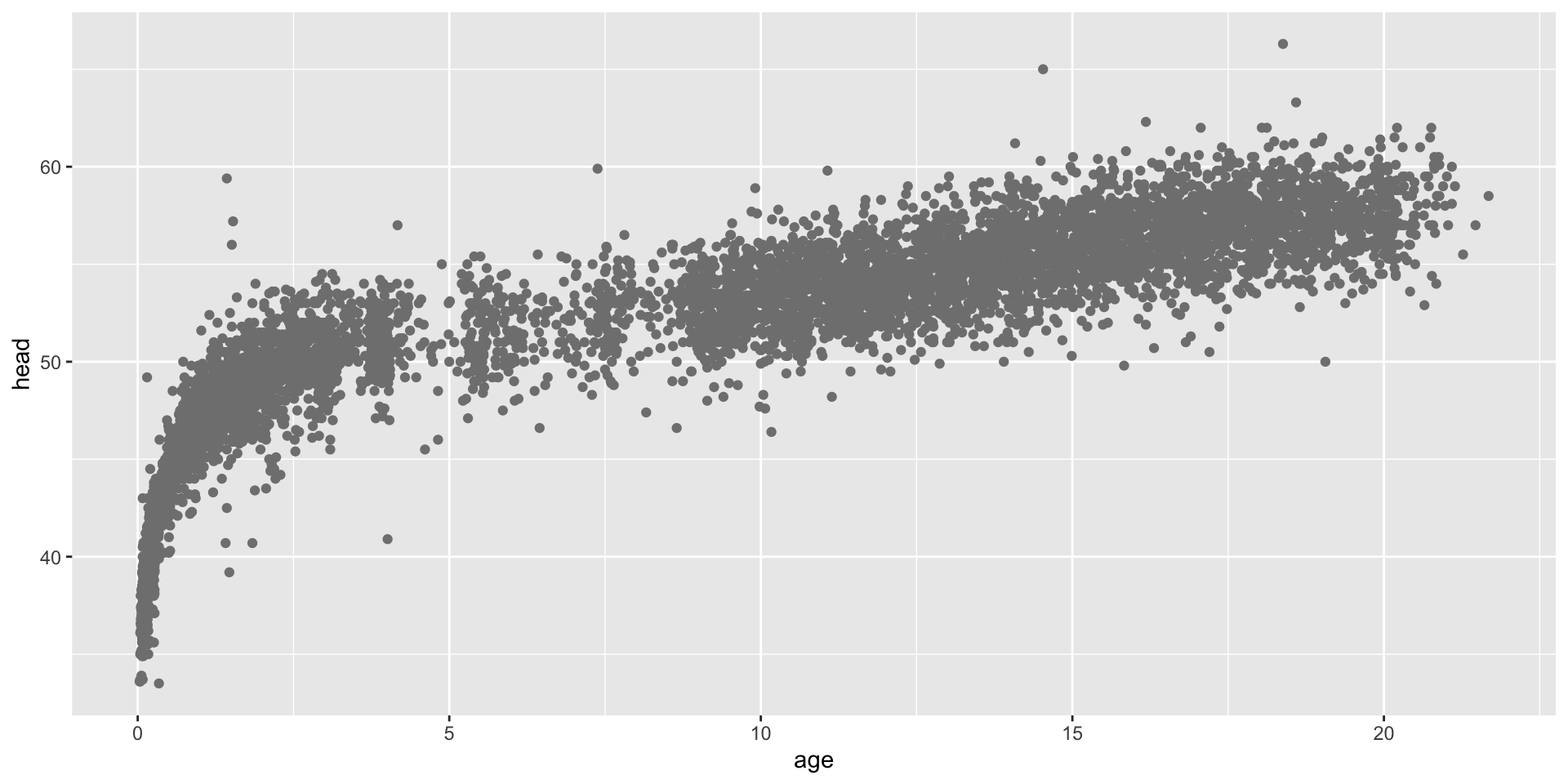
estimate the curves

library(gamlss2)
library(gamlss.ggplots)
 gBCTo <- gamlss2(head~s(I(age^.33))|s(I(age^.33))|s(I(age^.33))|s(I(age^.33)), 
                  data=db, family=BCTo, trace=FALSE)
fitted_centiles(gBCTo)

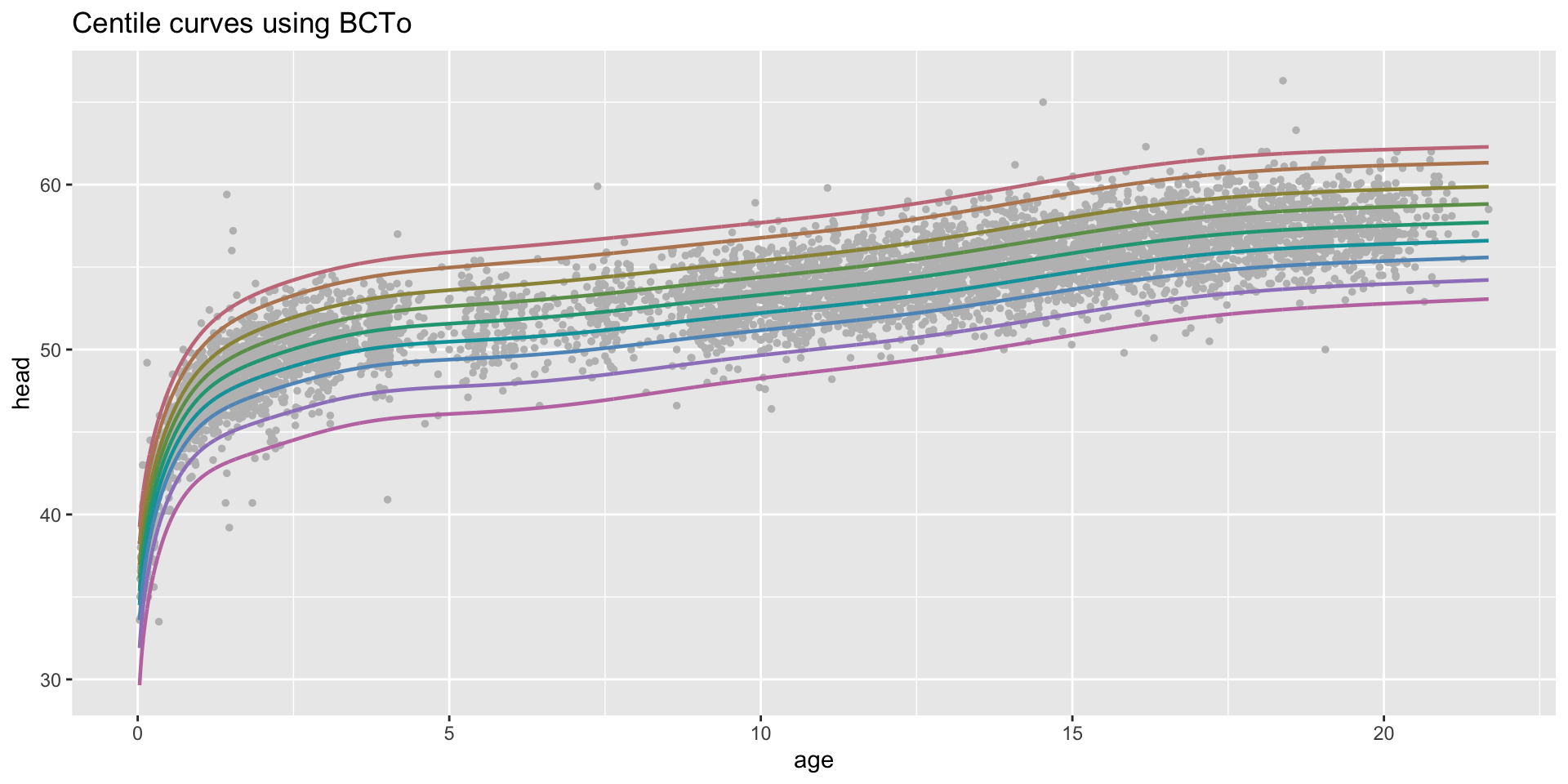
the target

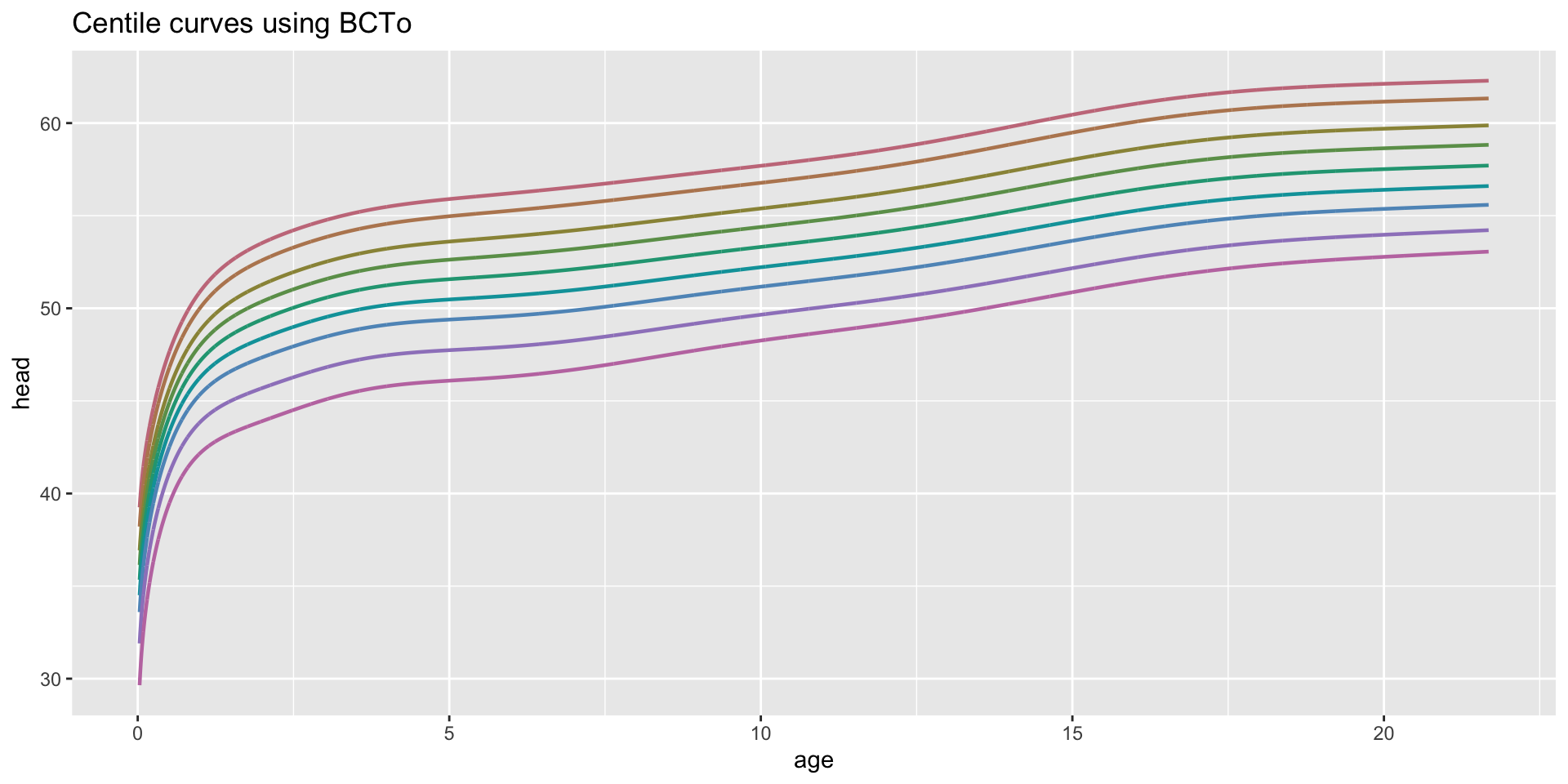
the methods

  • the non parametric approach of quantile regression (Koenker, 2005; Koenker and Bassett, 1978)

  • the parametric LMS approach of Cole (1988), Cole and Green (1992) and its extensions Rigby and Stasinopoulos (2004, 2006, 2007).

the LMS method

\[Y \sim f_Y(y| \mu, \sigma, \nu, \tau )\] where \(f_Y()\) is theoretical distribution,

  • \(y\) = head circumference and
  • \(x\) = age \(^\xi\)
  • \(\mu\) = s(x, \(df_\mu\))
  • \(\sigma\) = s(x, \(df_\sigma\))
  • \(\nu\) = s(x, \(df_\nu\))
  • \(\tau\) = s(x, \(df_\tau\))

the LMS method

\(y\) is defined through \(z\)

\[\begin{eqnarray} z = \frac{1}{\sigma \nu} \left[\left( \frac{y}{\mu}\right)^{\nu}-1 \right], & \ \textrm{if} \ \nu \neq 0 \nonumber \\ = \frac{1}{\sigma}\log\left(\frac{y}{\mu}\right), & \ \textrm{if} \ \nu =0. \nonumber \end{eqnarray}\]
  • if \(Z \sim N(0,1)\) then \(Y \sim BCCG(\mu, \sigma, \nu) =\) LMS method

LMS extentions

  • if \(Z \sim N(0,1)\) then \(Y \sim BCCG(\mu, \sigma, \nu) =\) LMS method

  • if \(Z \sim t_{\tau}\) then \(Y \sim BCT(\mu, \sigma, \nu, \tau)=\) LMST method

  • if \(Z \sim PE(0,1,\tau)\) then \(Y \sim BCPE(\mu, \sigma, \nu, \tau)=\) LMSP method adopted by WHO}

Box-Cox & Cole-Green transformation

Box-Cox& Cole-Green

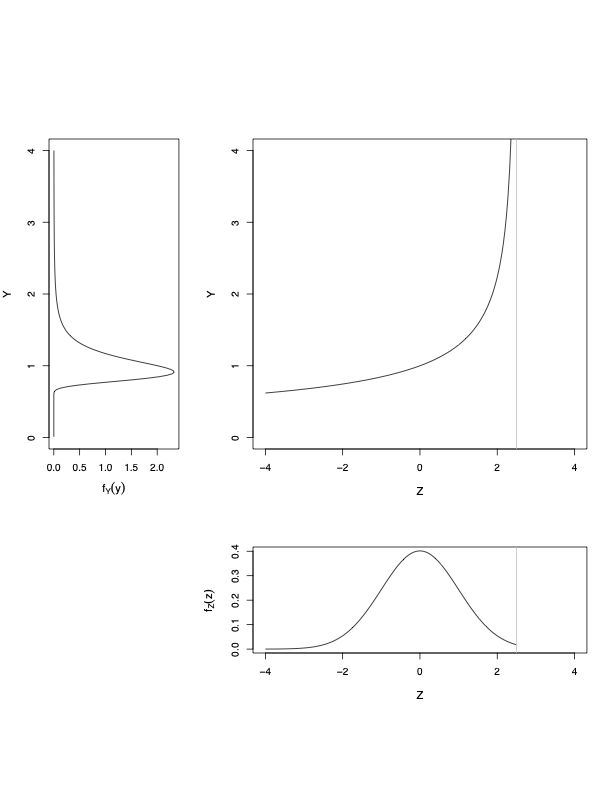
estimation of smoothing parameters

  • by trial and error

  • minimize the generalized Akaike information criterion, GAIC()

  • minimize the the validation global deviance VGD

  • using local selection criteria, i.e. CV, ML

procedure

  • select the transformation parameter \(\xi\)

  • fit different model and choose the minimim GAIC()

  • use diagnostic tools

  • get the centiles

transformation parameter \(\xi\)

library(gamlss2)
library(gamlss.ggplots)
gamlss.ggplots:::find_power(y=db$head, x=db$age, profile=TRUE, from=0, to=1, step=0.01)
*** Checking for transformation for x *** 
*** power parameters  0.24 ***  
[1] 0.24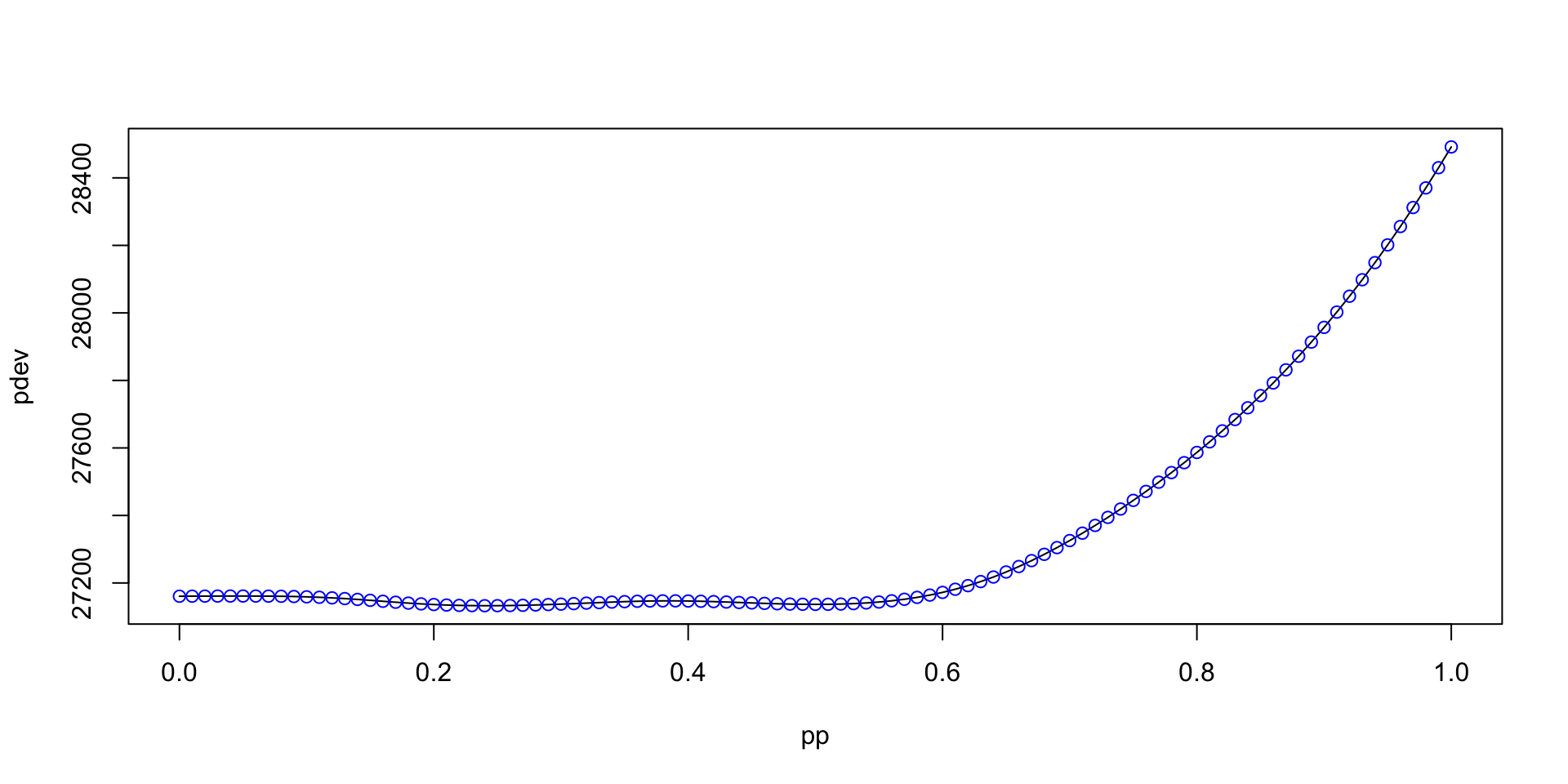

transformation parameter \(\xi\) (con.)

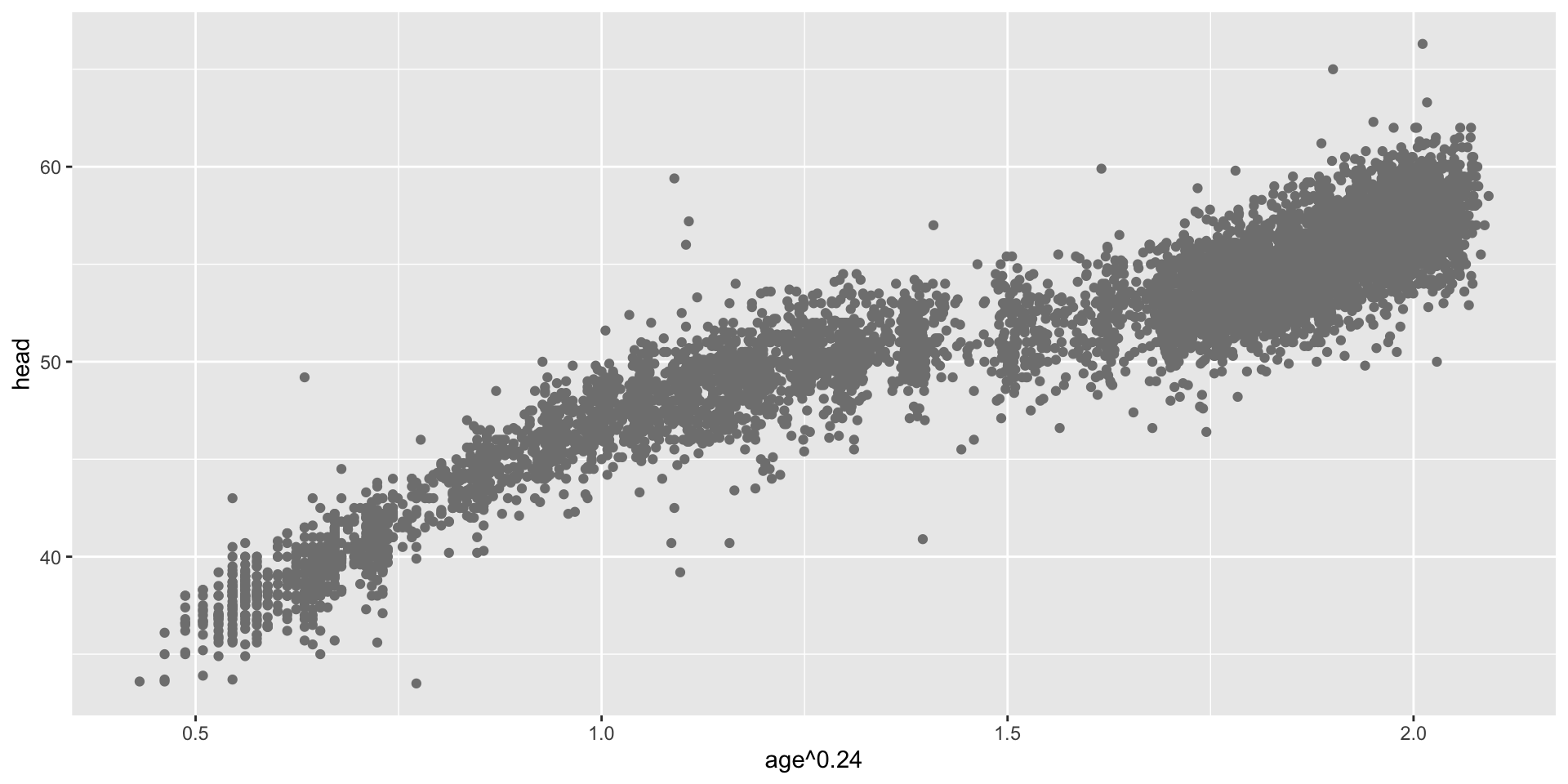
transformation parameter \(\xi\) (con.)

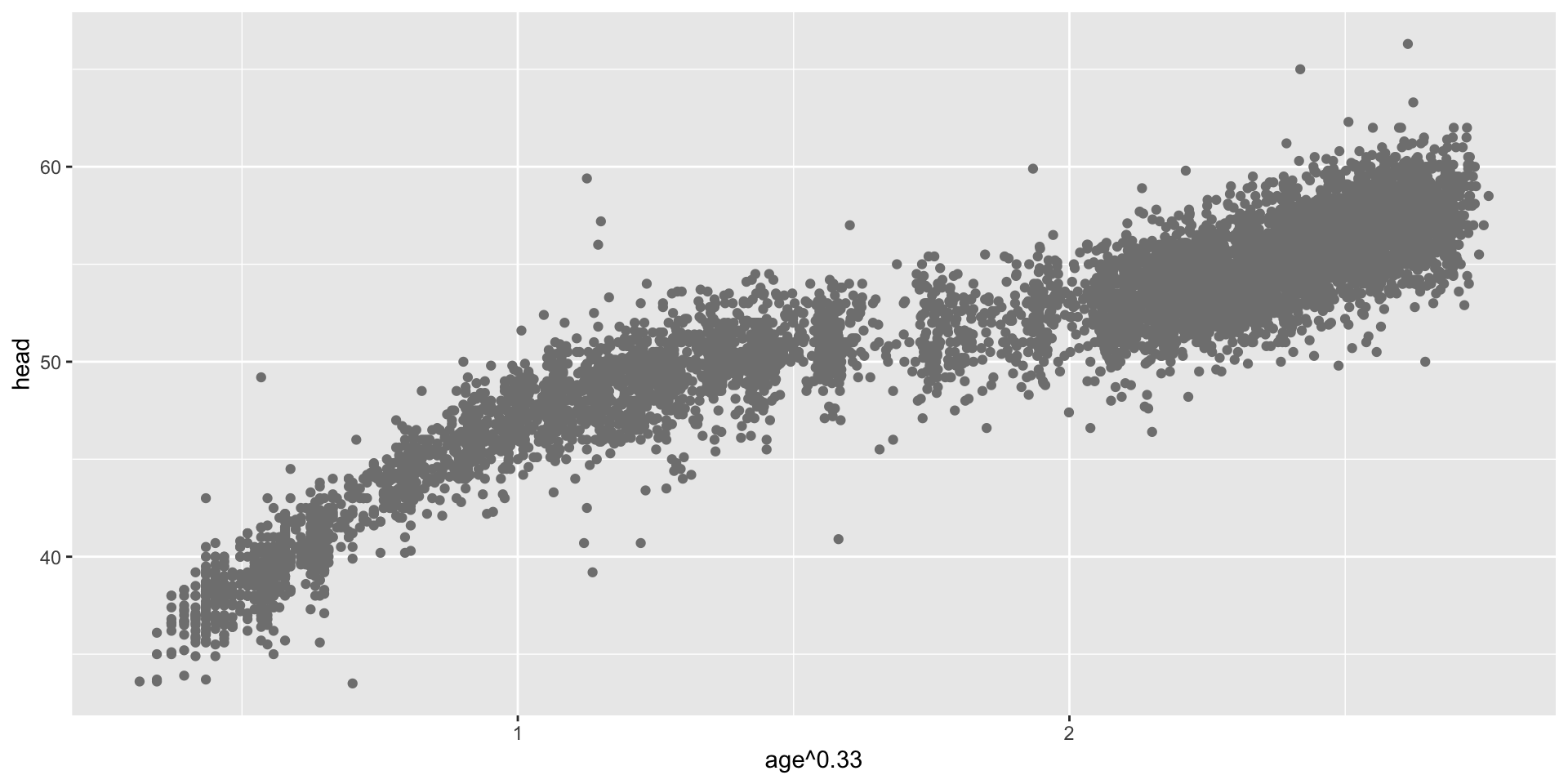
transformation parameter \(\xi\) (con.)

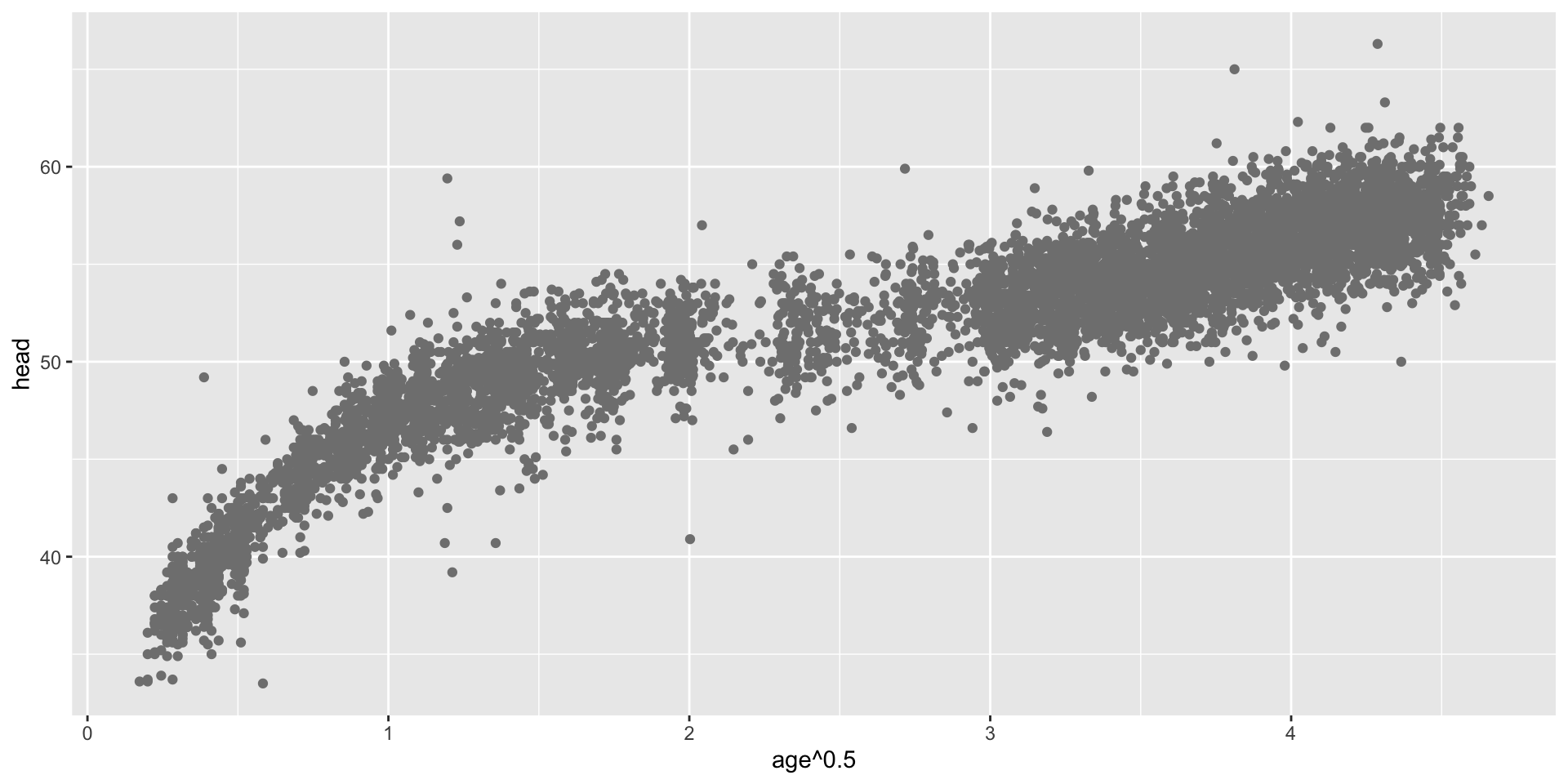
transformation parameter \(\xi\) (summary.)

  • smoothing techniques can not cope with sudden changes

  • if the sudden change is in the end of the data transforming using \(\xi\) could help

  • if the sudden change is in the middle a different transormation is required

  • alternatively using adapting smoothing parameter can help

fit different models

   gNO <- gamlss2(head~s(I(age^.33))|s(I(age^.33)), data=db, family=NO)
GAMLSS-RS iteration  1: Global Deviance = 27047.653 eps = 0.384661     
GAMLSS-RS iteration  2: Global Deviance = 27005.107 eps = 0.001573     
GAMLSS-RS iteration  3: Global Deviance = 27005.0941 eps = 0.000000     
 gBCCGo <- gamlss2(head~s(I(age^.33))|s(I(age^.33))|s(I(age^.33)), data=db, family=BCCGo)
GAMLSS-RS iteration  1: Global Deviance = 27134.2939 eps = 0.389668     
GAMLSS-RS iteration  2: Global Deviance = 26944.0924 eps = 0.007009     
GAMLSS-RS iteration  3: Global Deviance = 26941.8838 eps = 0.000081     
GAMLSS-RS iteration  4: Global Deviance = 26941.8334 eps = 0.000001     
 gBCPEo <- gamlss2(head~s(I(age^.33))|s(I(age^.33))|s(I(age^.33))|s(I(age^.33)), data=db, family=BCPEo)
GAMLSS-RS iteration  1: Global Deviance = 27412.103 eps = 0.377203     
GAMLSS-RS iteration  2: Global Deviance = 26825.7069 eps = 0.021391     
GAMLSS-RS iteration  3: Global Deviance = 26822.0093 eps = 0.000137     
GAMLSS-RS iteration  4: Global Deviance = 26821.9891 eps = 0.000000     
 gBCTo <- gamlss2(head~s(I(age^.33))|s(I(age^.33))|s(I(age^.33))|s(I(age^.33)), data=db, family=BCTo)
GAMLSS-RS iteration  1: Global Deviance = 26940.9697 eps = 0.390731     
GAMLSS-RS iteration  2: Global Deviance = 26749.7364 eps = 0.007098     
GAMLSS-RS iteration  3: Global Deviance = 26747.984 eps = 0.000065     
GAMLSS-RS iteration  4: Global Deviance = 26747.8873 eps = 0.000003

select models

gamlss2::GAIC(gNO, gBCTo, gBCPEo, gBCCGo)
            AIC       df
gBCTo  26792.07 22.08936
gBCPEo 26871.06 24.53565
gBCCGo 26998.12 28.14446
gNO    27042.92 18.91385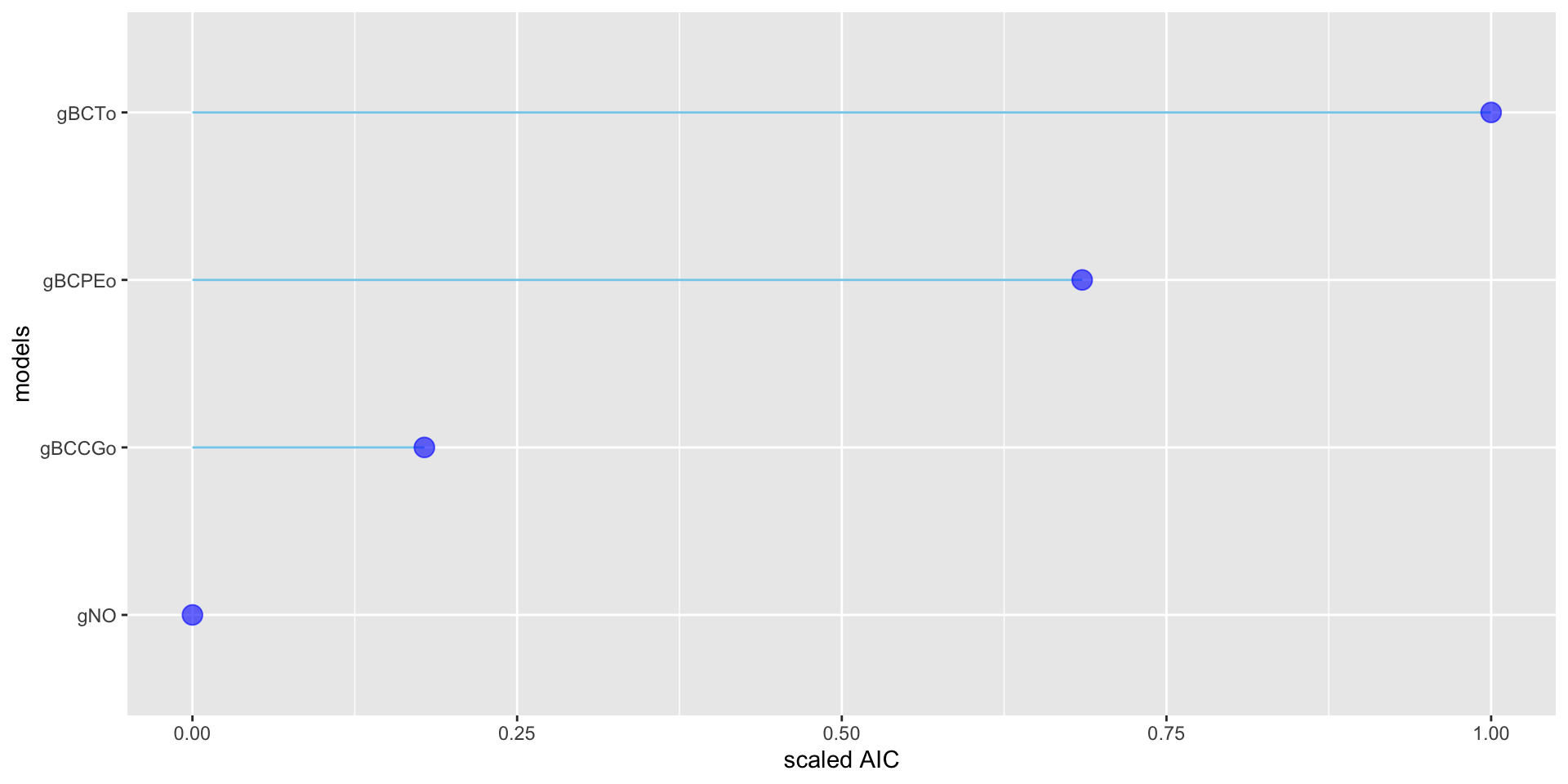
model_GAIC_lollipop(gNO, gBCTo, gBCPEo, gBCCGo)

diagnostic tools: residuals

resid_plots(gBCTo)

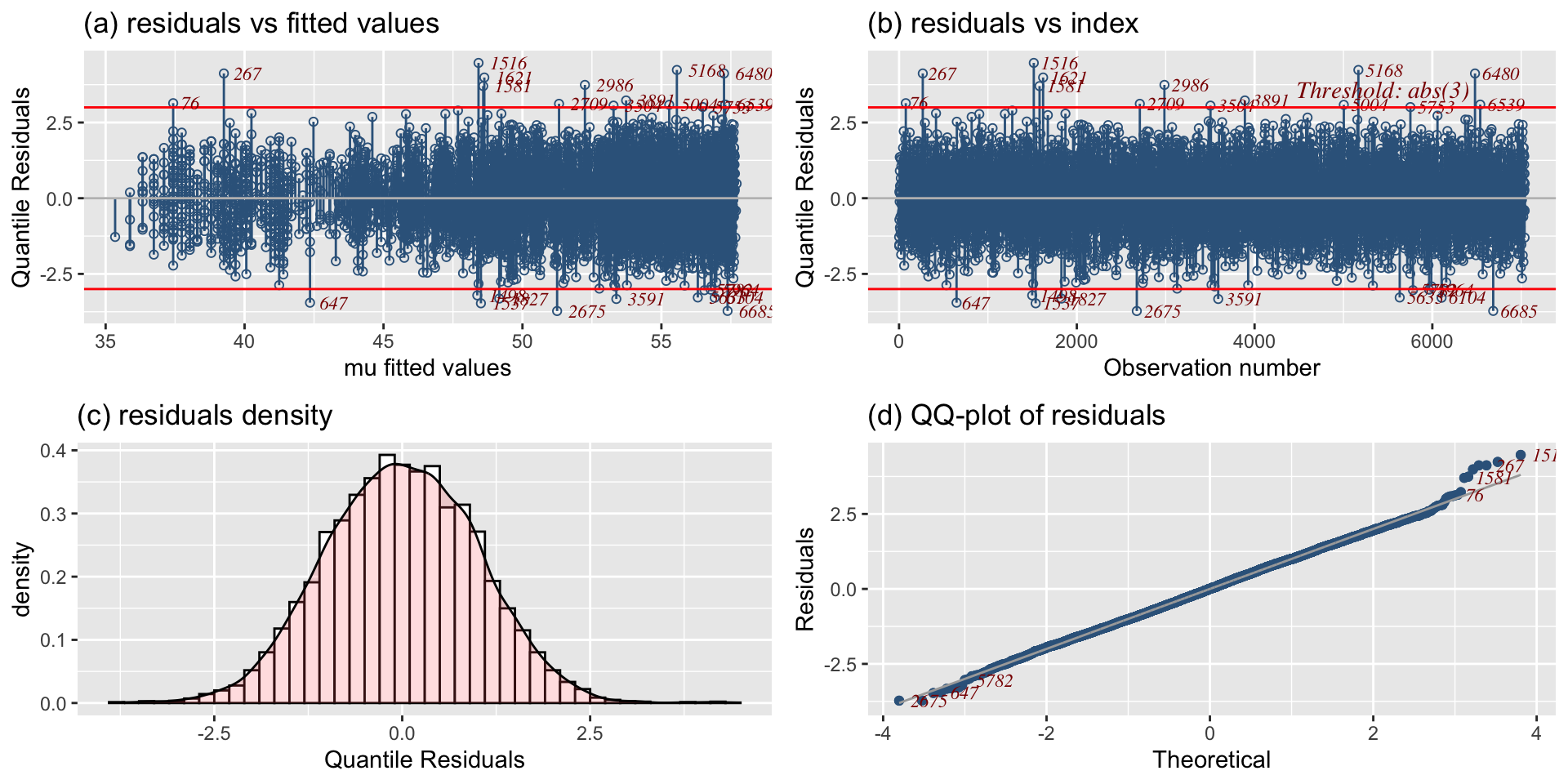
QQplot

resid_qqplot(gBCTo)

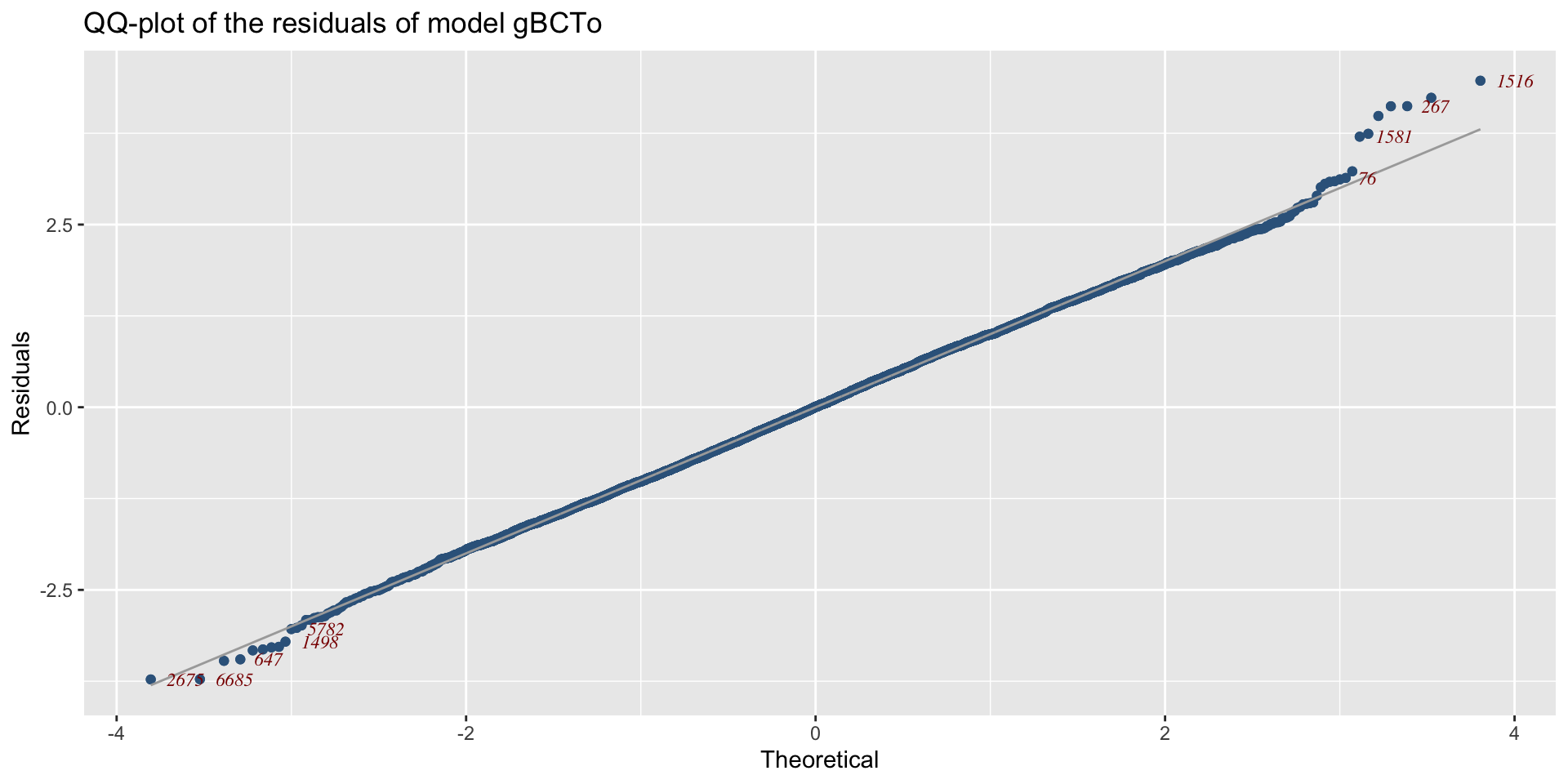
worm plots

resid_wp(gBCTo)

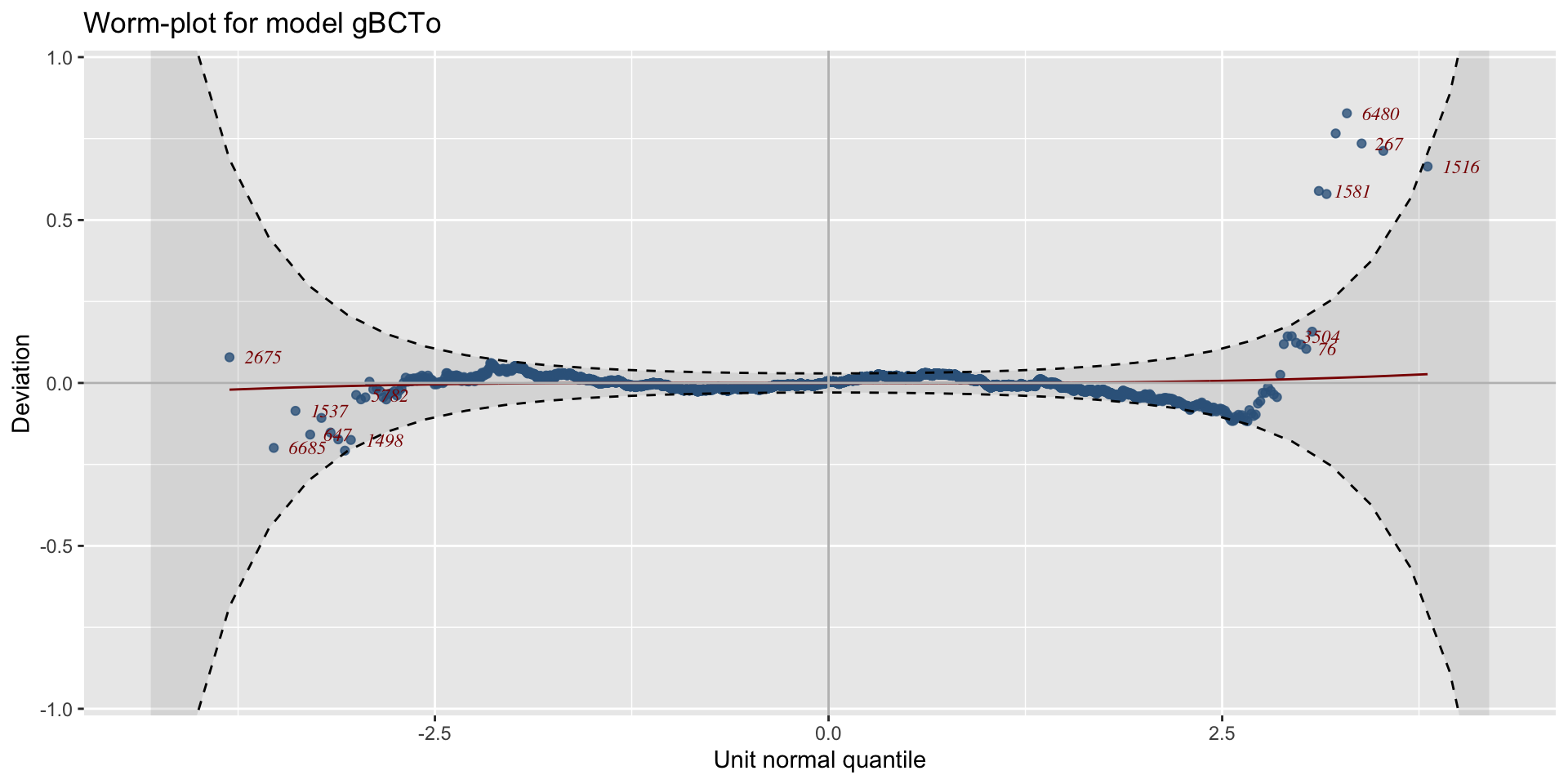
different models worm plots

model_wp(gBCTo, gNO)

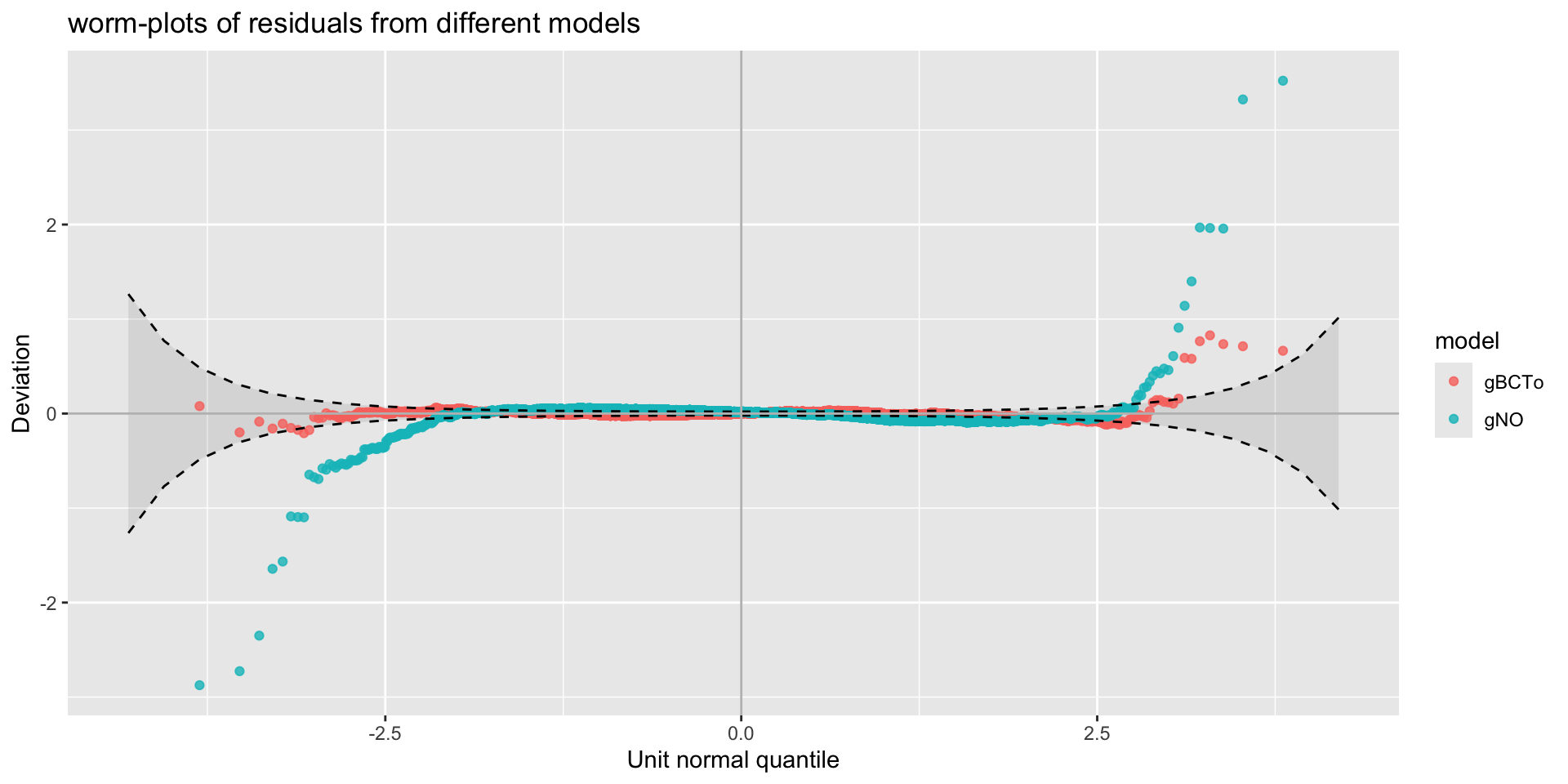
different x-values worm plots

resid_wp_wrap(gBCTo, xvar=db$age)

centiles

fitted_centiles(gBCTo)

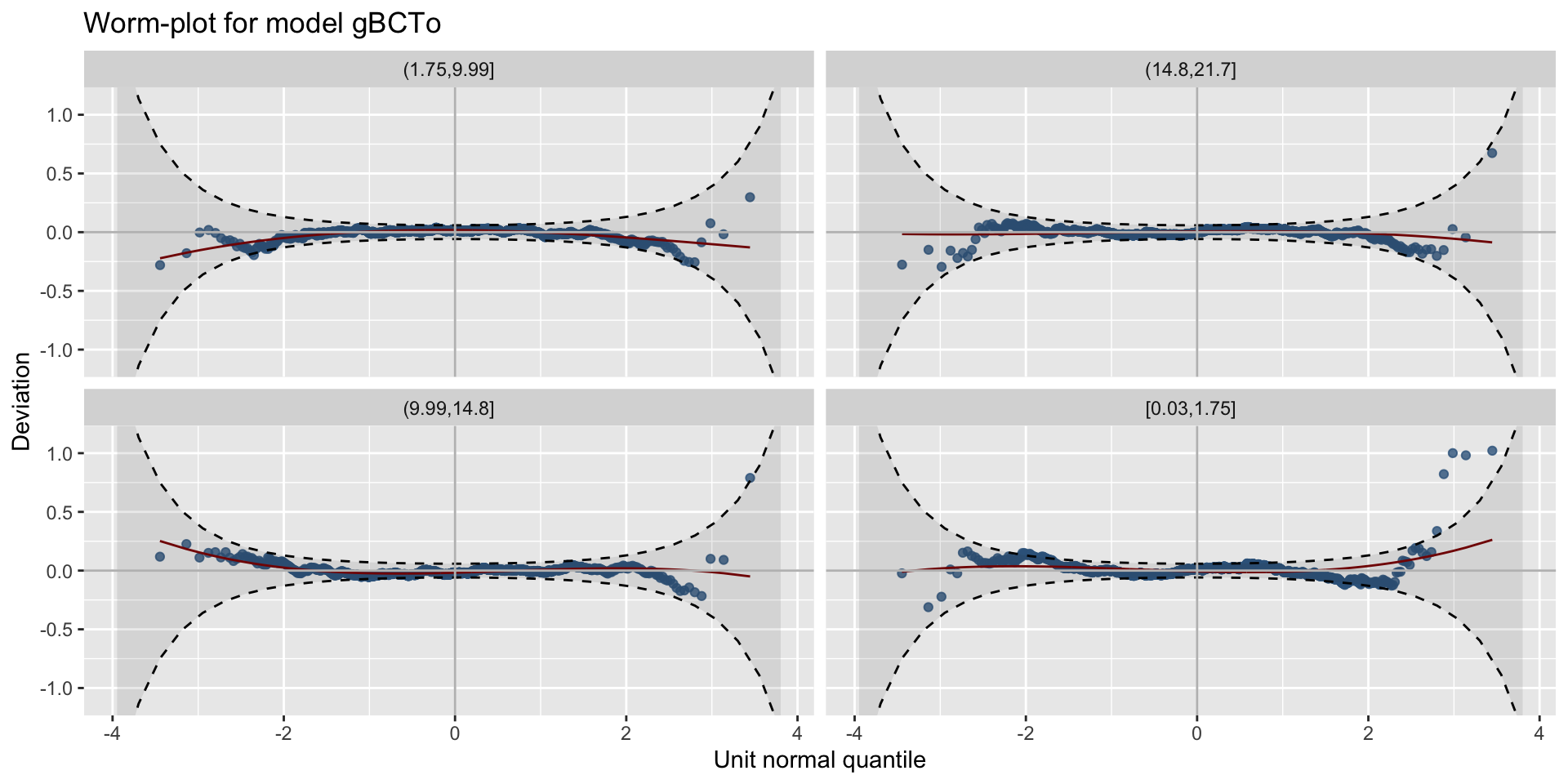
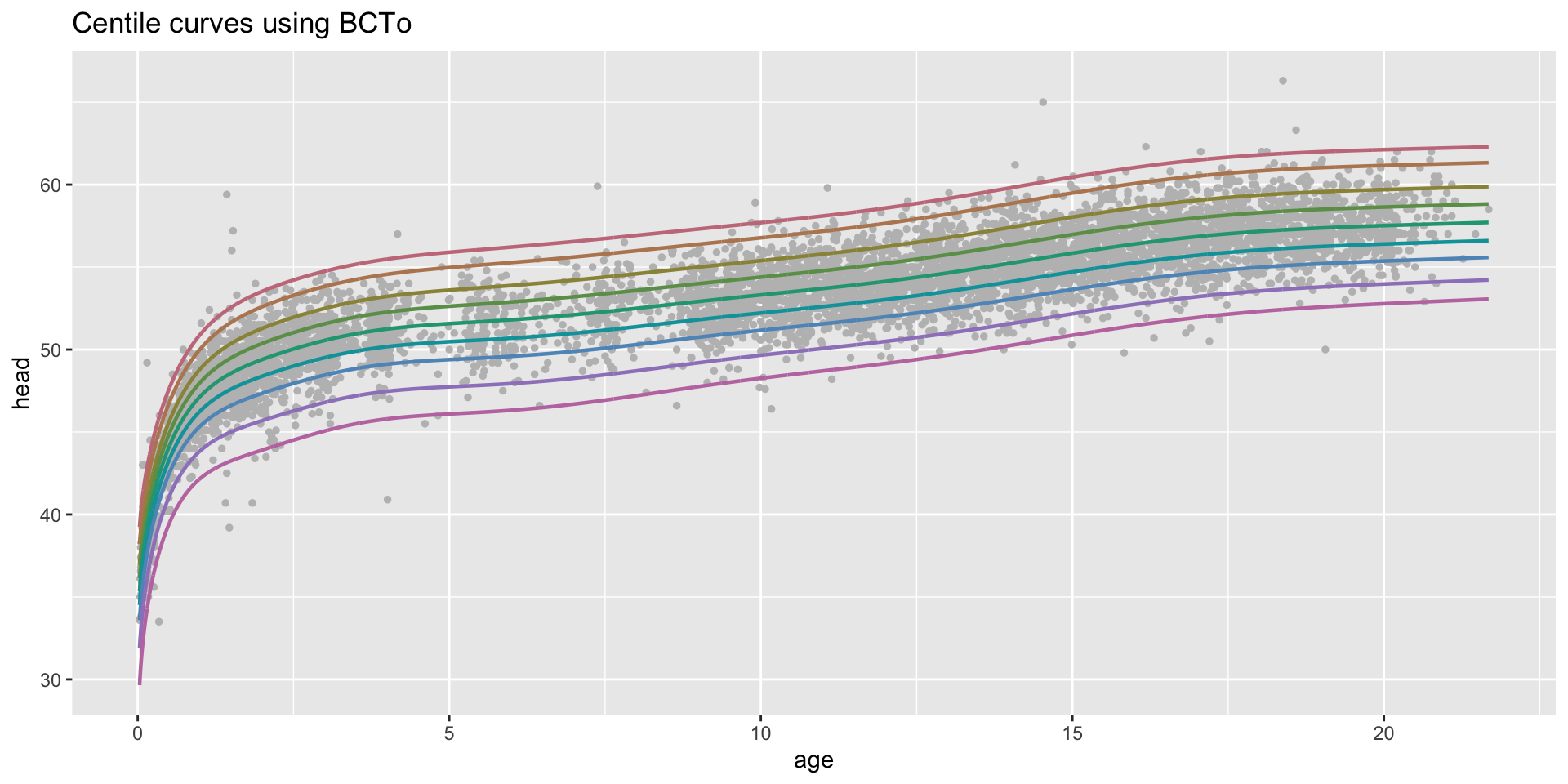
centiles just curves

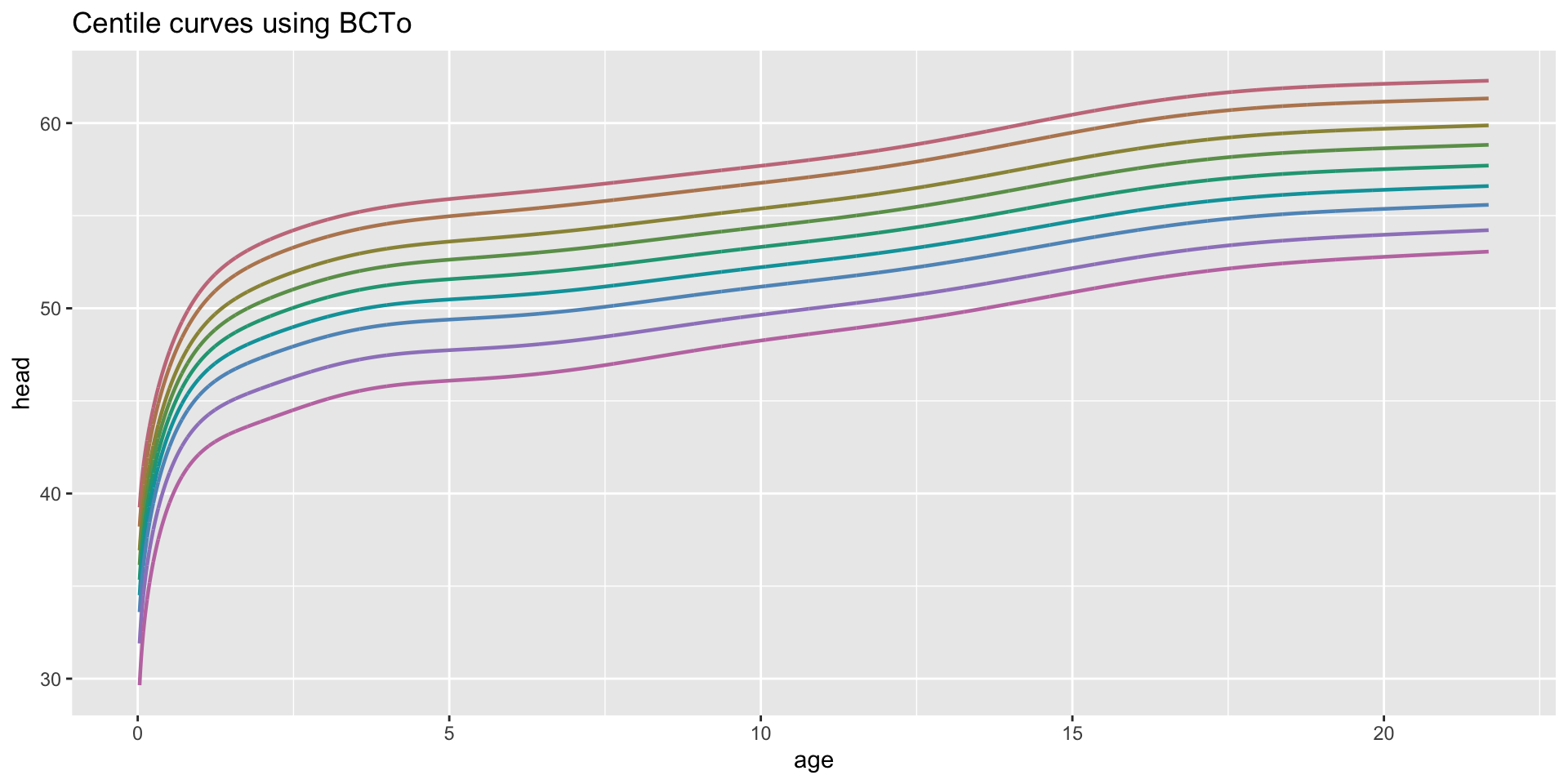
fitted_centiles(gBCTo, points=FALSE)

centiles with legend

fitted_centiles_legend(gBCTo)

centiles different models

model_centiles(gBCTo, gNO)

centiles different models in one plot

model_centiles(gBCTo, gNO, in.one=TRUE)

centiles different models in one plot

model_centiles(gBCTo, gNO, in.one=TRUE)

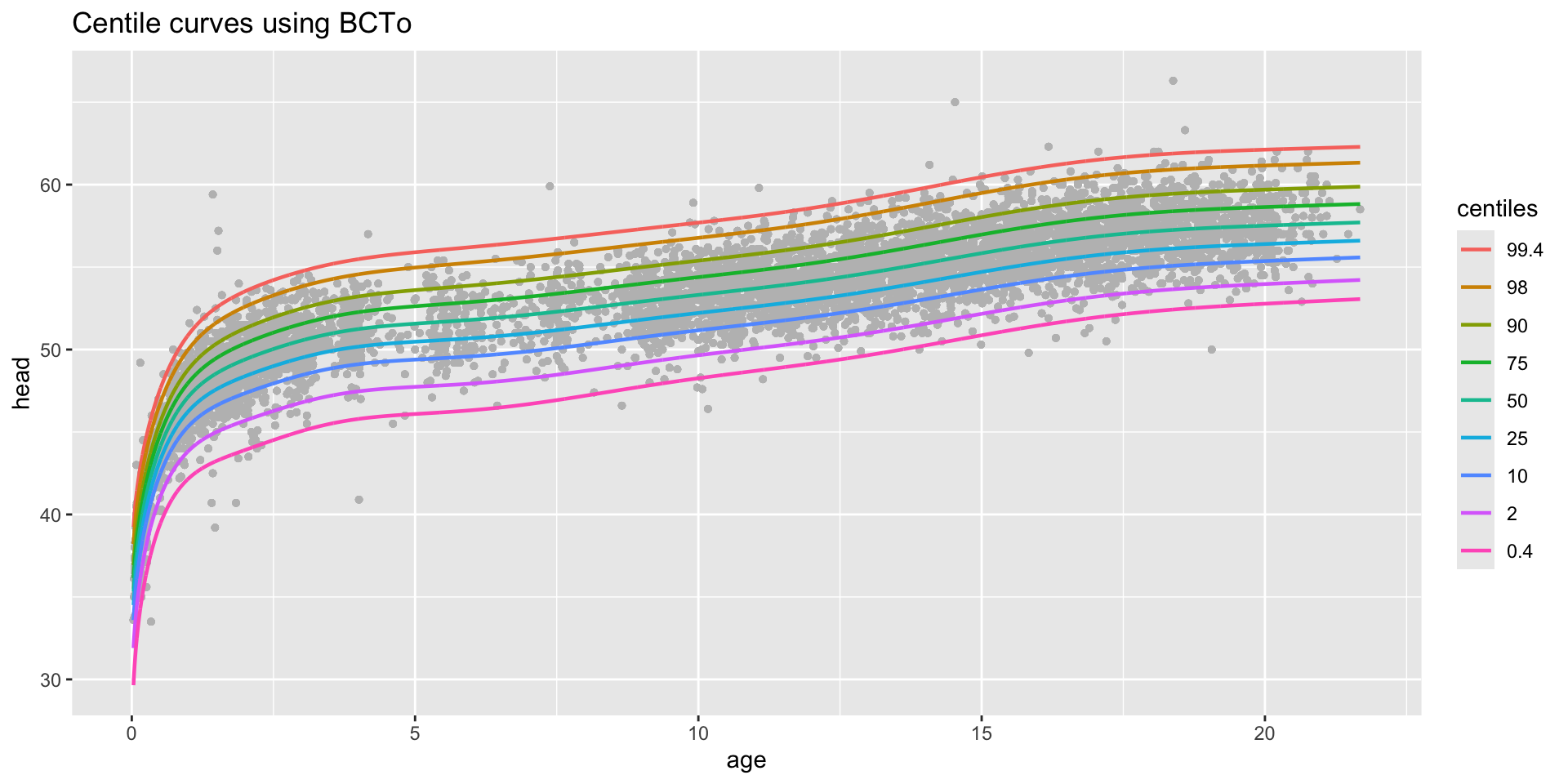
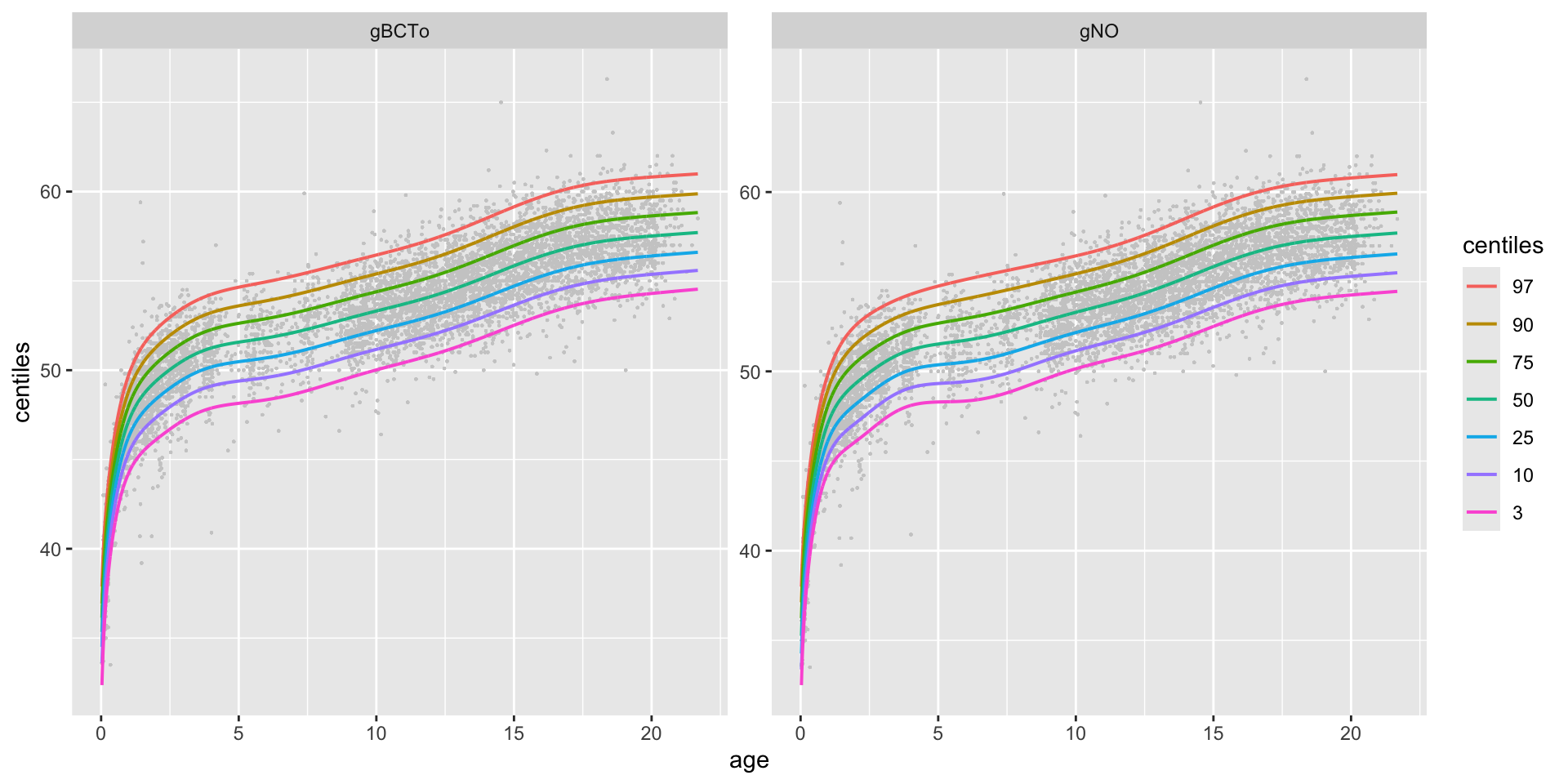
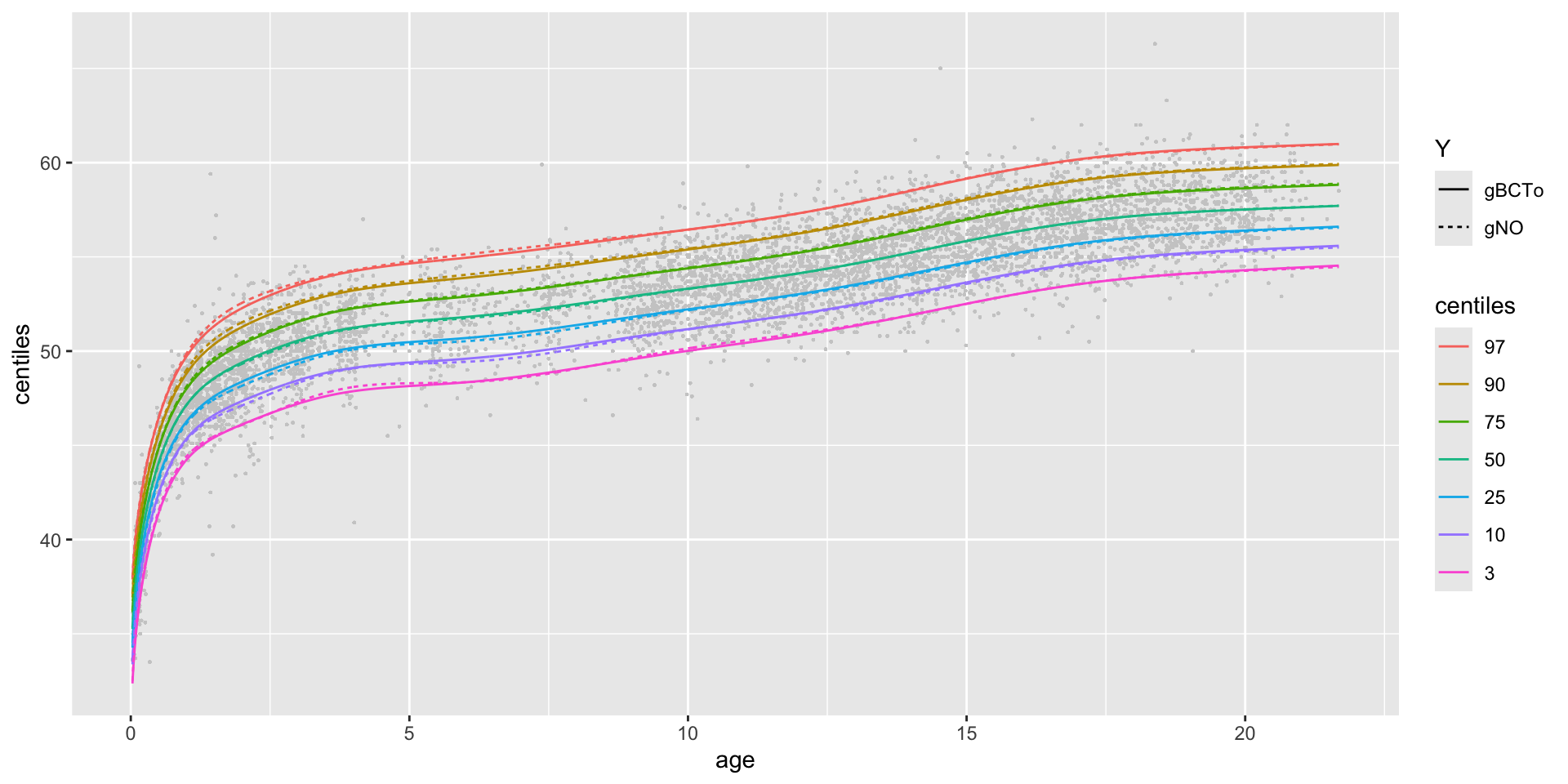
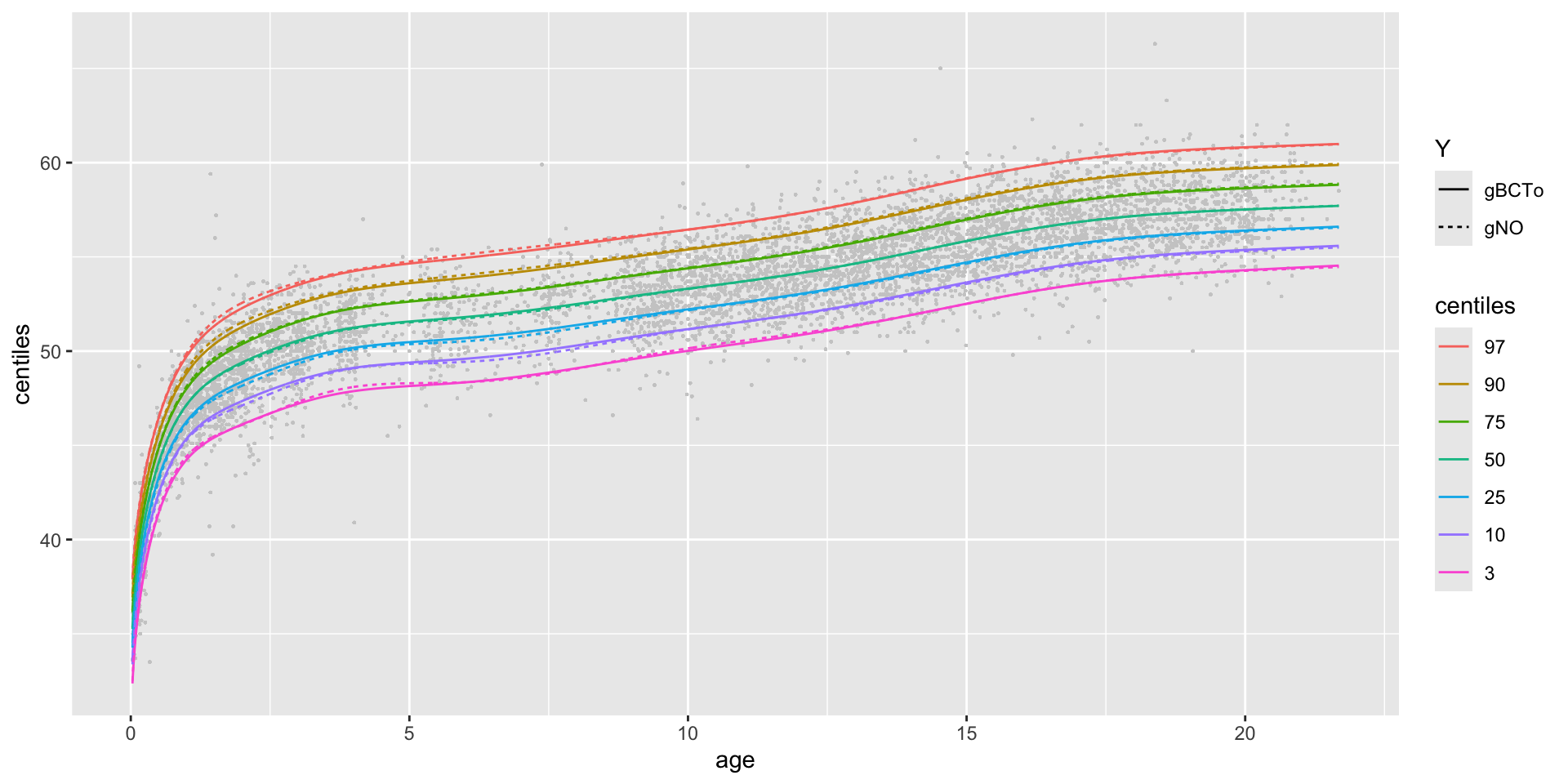
centiles different models different x-valus in one plot

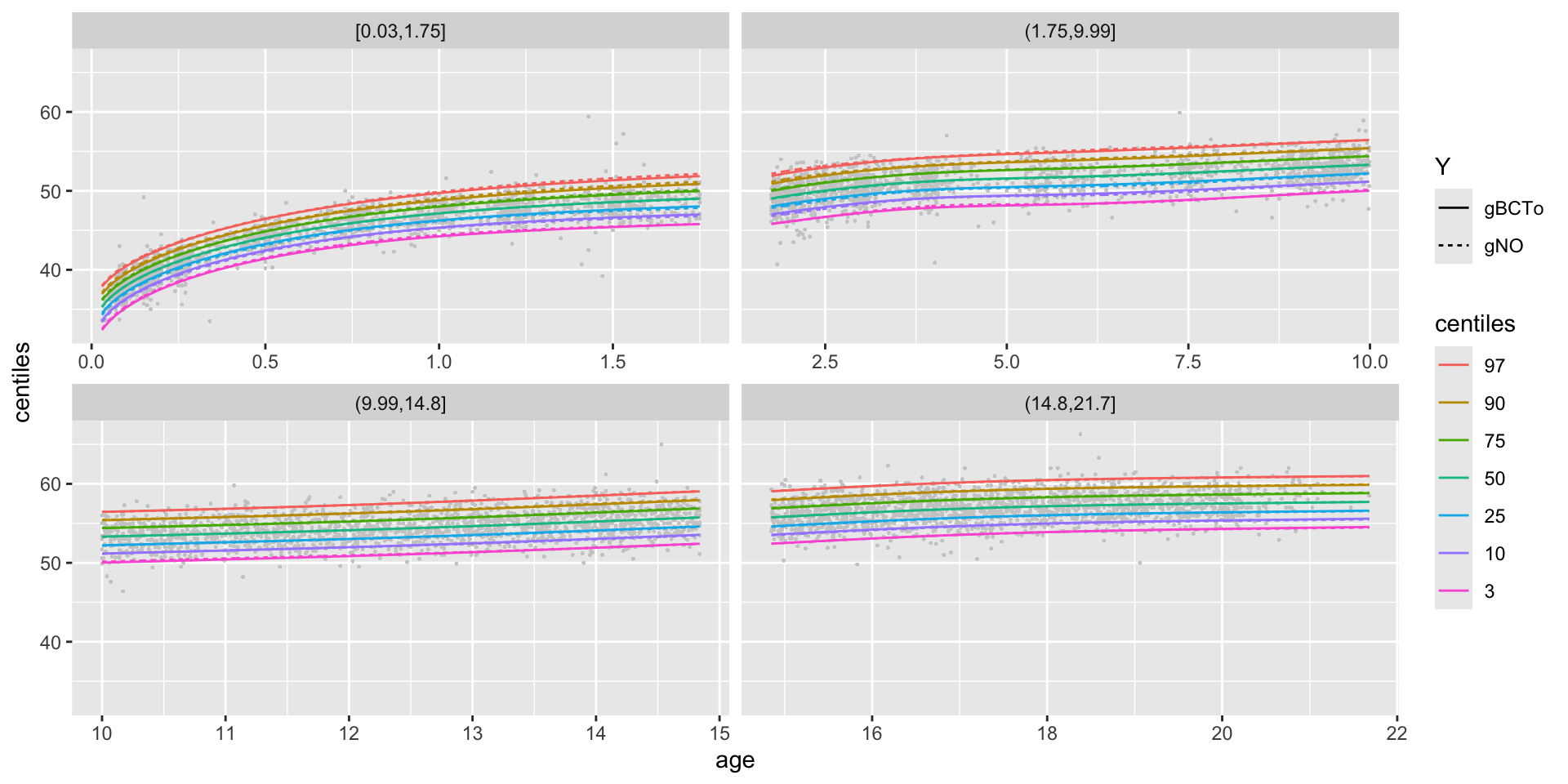
fitted parameters

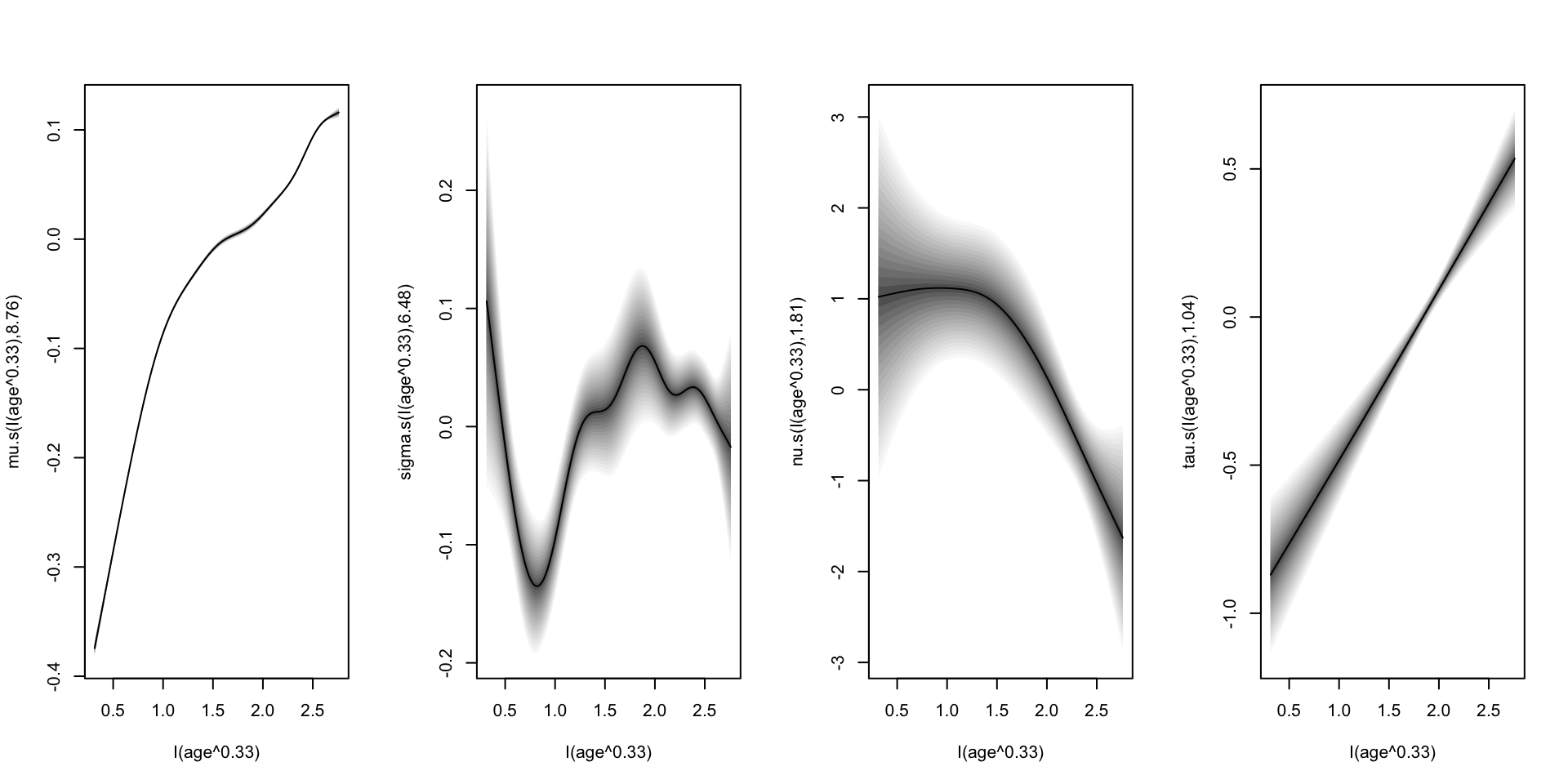
bucket plots

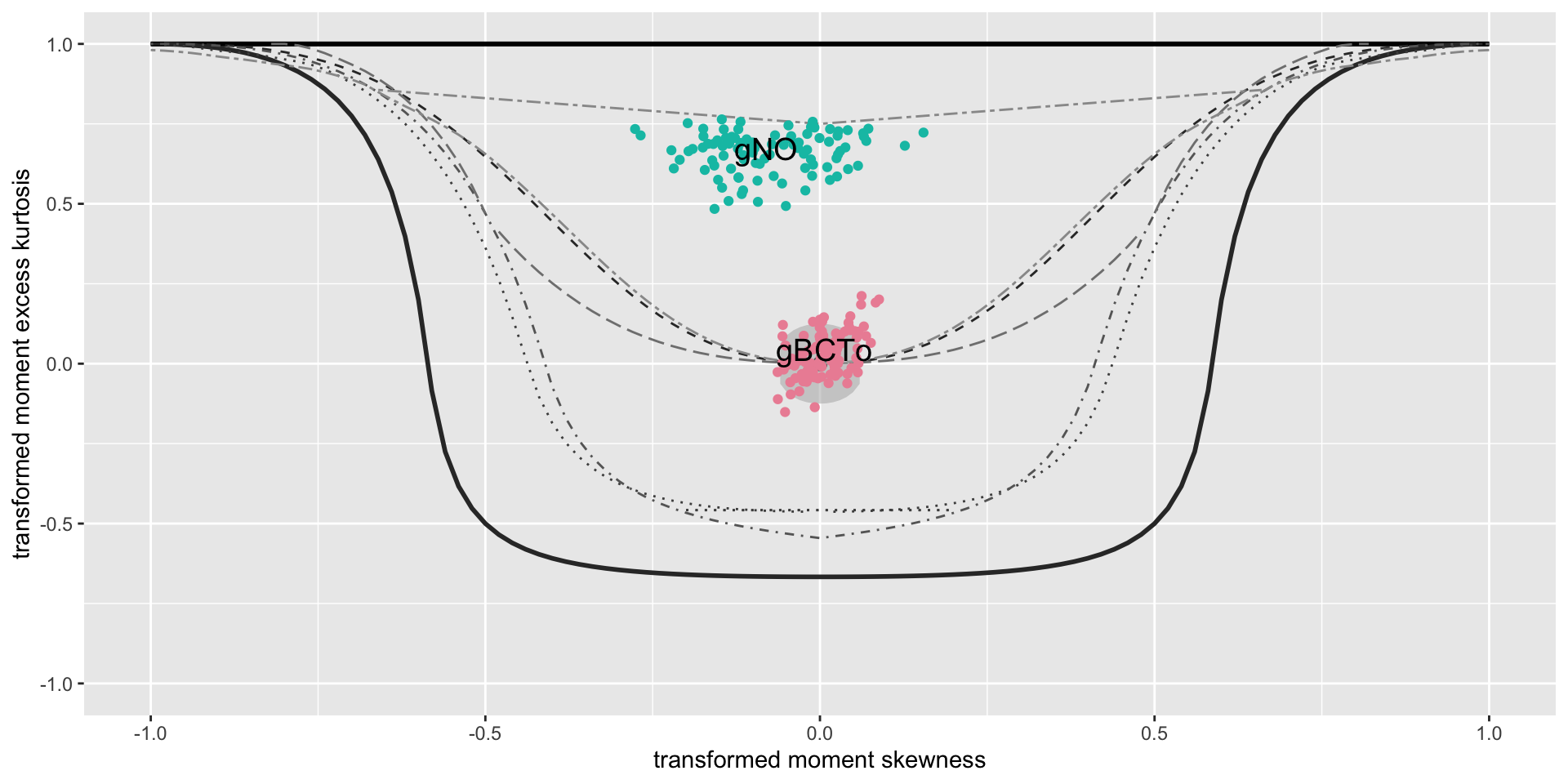
Q-stats

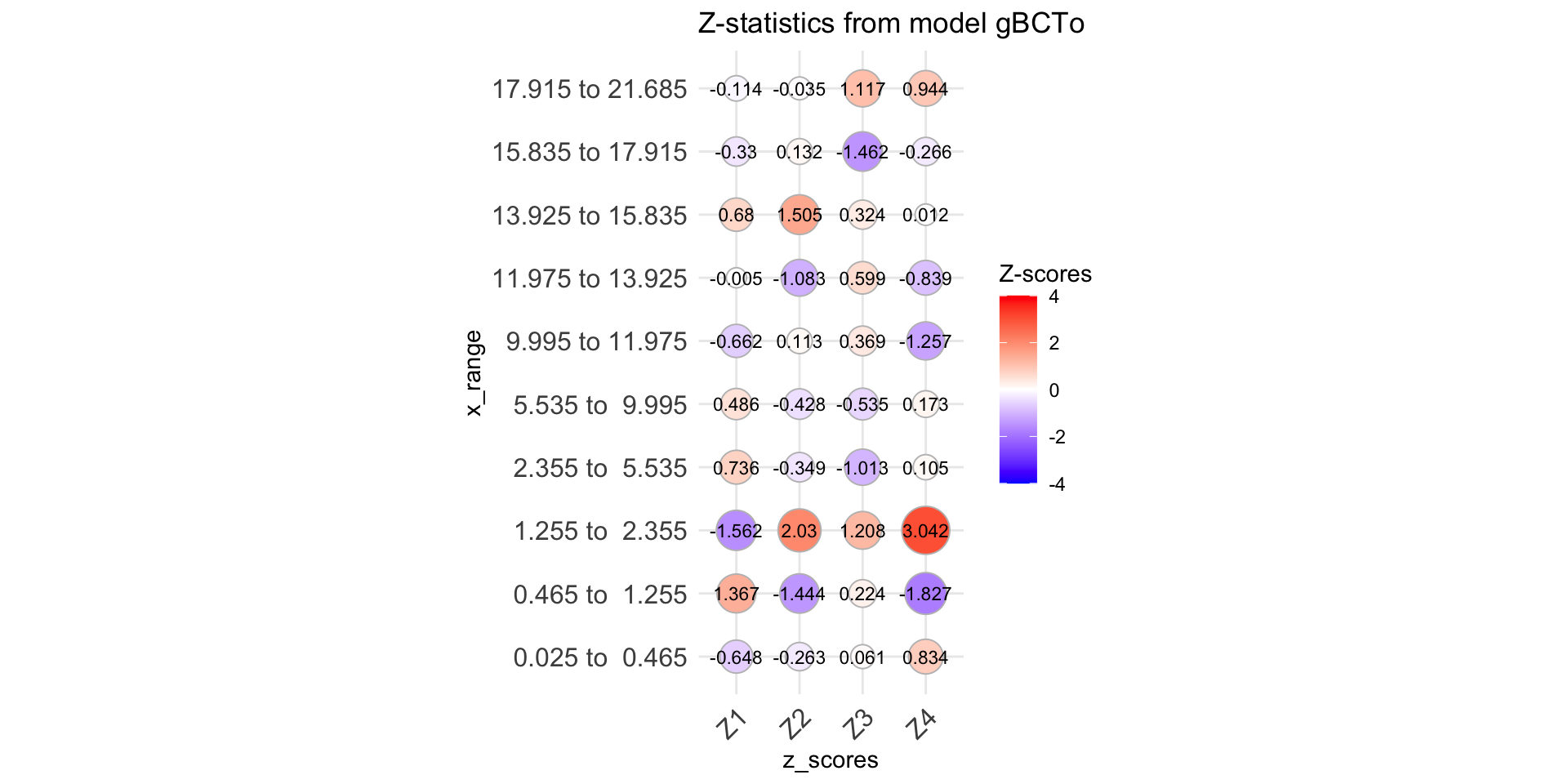
predict

library(broom)
library(knitr)
da <- predict(gBCTo, newdata=db[c(1, 1000, 2000, 3000, 6000,7000),])
da  |> head() |> kable(digits = c(2, 4, 4, 4), format="pipe")
mu sigma nu tau
1 35.34 0.0317 3.0297 4.8899
1042 46.10 0.0253 3.1266 6.8850
2091 49.50 0.0286 3.0847 8.3999
3118 52.27 0.0304 2.2706 12.3616
6327 56.82 0.0290 0.8780 17.5648
7422 57.57 0.0283 0.4968 19.3337

end

back to the index

The Books

www.gamlss.com